Canopy演算法是2000年由Andrew McCallum, Kamal Nigam and Lyle Ungar提出來的，它是對k-means聚類演算法和層次聚類演算法的預處理。眾所周知，kmeans的一個缺點在於k值需要透過人為的進行調整，後期可以透過肘部法則（Elbow Method）和輪廓係數（Silhouette Coefficient）來對k值進行最終的確定，但是這些方法都是屬於「事後」判斷的，而Canopy演算法的作用就在於它是透過事先粗聚類的方式，為k-means演算法確定初始聚類中心個數和聚類中心點。
使用的套件：
import math
import random
import numpy as np
from datetime import datetime
from pprint import pprint as p
import matplotlib.pyplot as plt
登入後複製
1.首先我在演算法中預設了一個二維（為了方便後期畫圖呈現在二維平面上）資料dataset。
當然也可以使用高緯度的數據，並且我將canopy核心演算法寫入了類別中，後期可以透過直接調用的方式對任何維度的數據進行處理，當然只是小批量的，大批量的資料可以移步Mahout和Hadoop了。
# 随机生成500个二维[0,1)平面点
dataset = np.random.rand(500, 2)
登入後複製
相關推薦：《Python影片教學》
#2.然後產生個兩類，類別的屬性如下：##
class Canopy:
def __init__(self, dataset):
self.dataset = dataset
self.t1 = 0
self.t2 = 0登入後複製
加入設定t1和t2初始值以及判斷大小函數
# 设置初始阈值
def setThreshold(self, t1, t2):
if t1 > t2:
self.t1 = t1
self.t2 = t2
else:
print('t1 needs to be larger than t2!')登入後複製
3.距離計算，各個中心點之間的距離計算方法我使用的歐式距離。
#使用欧式距离进行距离的计算
def euclideanDistance(self, vec1, vec2):
return math.sqrt(((vec1 - vec2)**2).sum())登入後複製
4.再寫個從dataset中根據dataset的長度隨機選擇下標的函數
# 根据当前dataset的长度随机选择一个下标
def getRandIndex(self):
return random.randint(0, len(self.dataset) - 1)登入後複製
5.核心演算法
def clustering(self):
if self.t1 == 0:
print('Please set the threshold.')
else:
canopies = [] # 用于存放最终归类结果
while len(self.dataset) != 0:
rand_index = self.getRandIndex()
current_center = self.dataset[rand_index] # 随机获取一个中心点，定为P点
current_center_list = [] # 初始化P点的canopy类容器
delete_list = [] # 初始化P点的删除容器
self.dataset = np.delete(
self.dataset, rand_index, 0) # 删除随机选择的中心点P
for datum_j in range(len(self.dataset)):
datum = self.dataset[datum_j]
distance = self.euclideanDistance(
current_center, datum) # 计算选取的中心点P到每个点之间的距离
if distance < self.t1:
# 若距离小于t1，则将点归入P点的canopy类
current_center_list.append(datum)
if distance < self.t2:
delete_list.append(datum_j) # 若小于t2则归入删除容器
# 根据删除容器的下标，将元素从数据集中删除
self.dataset = np.delete(self.dataset, delete_list, 0)
canopies.append((current_center, current_center_list))
return canopies登入後複製
為了方便後面的資料視覺化，我這裡的canopies定義的是一個數組，當然也可以使用dict。
6.main()函數
def main():
t1 = 0.6
t2 = 0.4
gc = Canopy(dataset)
gc.setThreshold(t1, t2)
canopies = gc.clustering()
print('Get %s initial centers.' % len(canopies))
#showCanopy(canopies, dataset, t1, t2)登入後複製
Canopy聚類視覺化程式碼
def showCanopy(canopies, dataset, t1, t2):
fig = plt.figure()
sc = fig.add_subplot(111)
colors = ['brown', 'green', 'blue', 'y', 'r', 'tan', 'dodgerblue', 'deeppink', 'orangered', 'peru', 'blue', 'y', 'r', 'gold', 'dimgray', 'darkorange', 'peru', 'blue', 'y', 'r', 'cyan', 'tan', 'orchid', 'peru', 'blue', 'y', 'r', 'sienna']
markers = ['*', 'h', 'H', '+', 'o', '1', '2', '3', ',', 'v', 'H', '+', '1', '2', '^', '<', '>', '.', '4', 'H', '+', '1', '2', 's', 'p', 'x', 'D', 'd', '|', '_'] for i in range(len(canopies)):
canopy = canopies[i]
center = canopy[0]
components = canopy[1]
sc.plot(center[0], center[1], marker=markers[i],
color=colors[i], markersize=10)
t1_circle = plt.Circle(
xy=(center[0], center[1]), radius=t1, color='dodgerblue', fill=False)
t2_circle = plt.Circle(
xy=(center[0], center[1]), radius=t2, color='skyblue', alpha=0.2)
sc.add_artist(t1_circle)
sc.add_artist(t2_circle) for component in components:
sc.plot(component[0], component[1],
marker=markers[i], color=colors[i], markersize=1.5)
maxvalue = np.amax(dataset)
minvalue = np.amin(dataset)
plt.xlim(minvalue - t1, maxvalue + t1)
plt.ylim(minvalue - t1, maxvalue + t1)
plt.show()登入後複製
效果圖如下：
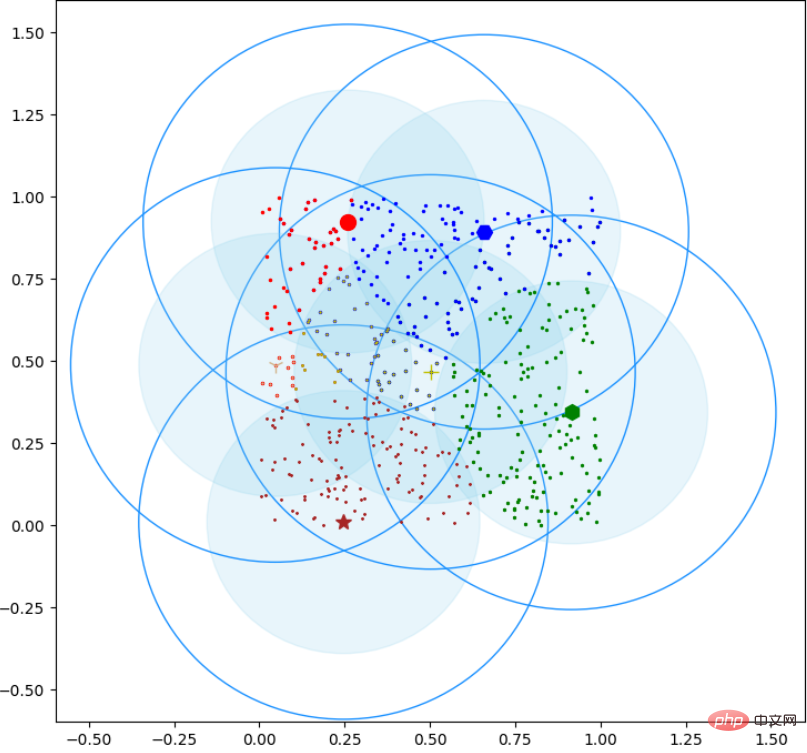
以上是python怎麼實作canopy聚類的詳細內容。更多資訊請關注PHP中文網其他相關文章！
