double浮點數運算為啥會失去精確度

前言:在工作中,談到有小數點的加減乘除都會想到用BigDecimal來解決,但是有很多人對於double或者float為啥會丟失精度一臉茫然。還有BigDecimal是怎麼解決的?話不多說,我們開始吧。
1.浮點數是啥?
浮點數是電腦用來表示小數的資料型,採用科學計數法。在java中,double是雙精度,64位,浮點數,預設是0.0d。 float是單一精確度,32位元.浮點數,預設為0.0f;

double 尾數(23 bit)
double 符號位元(1bit) 關係式(11 bit) 尾數(52 bit)
float在記憶體中指數是8bit,由於階碼實際儲存的是
float,記憶體中指數是8bit,由於階碼實際儲存的是##float指數的移碼,假設指數的真值是e,階碼為E,則有E=e (2^n-1 -1)。其中 2^n-1 -1是IEEE754標準規定的指數偏移量,根據這個公式我們可以得到 2^8 -1=127。於是,float的指數範圍為-128 127,而double的指數範圍為-1024 1023。其中負指數決定了浮點數所能表達的絕對值最小的非零數;而正指數決定了浮點數所能表達的絕對值最大的數,也即決定了浮點數的值範圍。
float的範圍為-2^128 ~ 2^127,也即-3.40E 38 ~ 3.40E 38;
double的範圍為-2^1024 ~ 2^1023,也即-1.79E 308 ~ 1.79E 3082.走進失真之科學計數法 我們先說說科學計數法,科學計數法是一種簡化計數的方法,用來近似表示一個極大或極小且位數較多的數,對於位數較小的數值,科學計數法沒有什麼優勢,但對於位數較多的數值其計數方法的優勢就非常明顯了。例如:光的速速是300000000公尺/秒,全世界人口數大約是6100000000。類似光的速度和世界人口數這樣大數值的數,讀、寫都很不方便,所以光的速度可以寫成3*10^8,全世界人口數可以寫成6.1*10^9。所以計算機用科學計數法表示光速是3E8,世界人口數大約是6.1E9。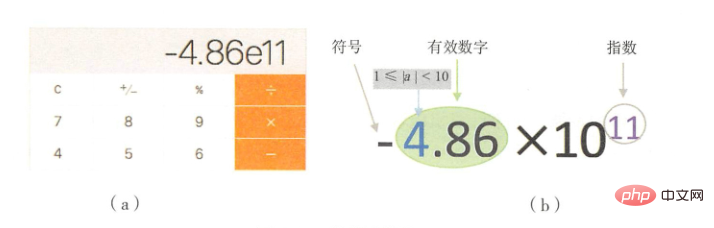 我們小時候玩計算器喜歡瘋狂的累加或累減,到最後計算器就會顯示下圖。這就是科學計數法顯示的結果
我們小時候玩計算器喜歡瘋狂的累加或累減,到最後計算器就會顯示下圖。這就是科學計數法顯示的結果
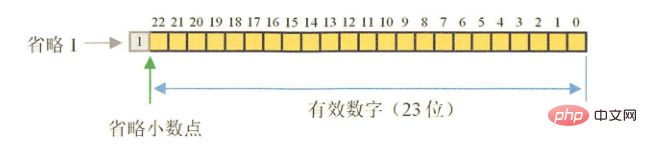 電腦在處理資料都涉及到資料的轉換和各種複雜運算,例如,不同單位換算,不同進制(如二進制十進制)換算等,很多除法運算不能除盡,例如10÷3=3.3333.....無窮無盡,而精度是有限的,3.3333333x3並不等於10,經過複雜的處理後得到的十進制數據並不精確,精度越高越精確。 float和double的精度是由尾數的位數來決定的,其整數部分始終是一個隱含著的“1”,由於它是不變的,故不能對精度造成影響。 float:2^23 = 8388608,一共七位,由於最左為1的一位省略了,這意味著最多能表示8位數: 28388608 = 167777216 。有8位有效數字,但絕對能保證的為7位,也即float的精度為7~8位有效數字;double:2^52 = 4503599627370496,一共16位,同理,double的精度為16~17位元.
電腦在處理資料都涉及到資料的轉換和各種複雜運算,例如,不同單位換算,不同進制(如二進制十進制)換算等,很多除法運算不能除盡,例如10÷3=3.3333.....無窮無盡,而精度是有限的,3.3333333x3並不等於10,經過複雜的處理後得到的十進制數據並不精確,精度越高越精確。 float和double的精度是由尾數的位數來決定的,其整數部分始終是一個隱含著的“1”,由於它是不變的,故不能對精度造成影響。 float:2^23 = 8388608,一共七位,由於最左為1的一位省略了,這意味著最多能表示8位數: 28388608 = 167777216 。有8位有效數字,但絕對能保證的為7位,也即float的精度為7~8位有效數字;double:2^52 = 4503599627370496,一共16位,同理,double的精度為16~17位元.
 如遇到
如遇到
double型別 0.3-0.1的情況。需要將0.3轉成二進位在運算
0.3 * 2 = 0.6 => .0 (.6)取0剩0.6
0.6 * 2 = 1.2 => .01 (. 2)取1剩0.2
0.2 * 2 = 0.4 => .010 (.4)取0剩0.4

3.總結
看完上面,大概清楚了為啥浮點數會有精確度問題。簡單來說float和double類型主要是為了科學計算和工程計算而設計,他們執行二進制浮點運算,這是為了在廣泛的數值範圍上提供較為精確的快速近和計算而精心設計的。然而,他們並沒有提供完全精確的結果,所以不應該被用於精確的結果的場合。浮點數達到一定大的數會自動使用科學計數法,這樣的表示只是近似真實數而不等於真實數。當十進制小數位轉換二進制的時候也會出現無限循環或超過浮點數尾數的長度。
4.那我們要怎麼用BigDecimal來解?
大家看下面的兩個輸出

輸出結果:
0.299999999999999988897769753748434595763683319091796832##.阿里的程式碼約束外掛程式已經標註警告,讓我使用String參數的建構方法來建立BigDecimal。因為double不能精確地表示為0.3(任何有限長度的二進位),所以構造方法傳遞的值也是不完全等於0.3。大家在使用BigDecimal的時候一定要用String參數的建構方法來建立。說到這裡,是木頭有還有好奇的寶寶有疑問,BigDecimal的原理是啥?為啥它就沒有問題呢?其實原理很簡單,BigDecimal是不可變的,可以用來表示任意精確度的帶符號十進位數。 double之所以會出問題,是因為小數點轉二進位遺失精確度。 BigDecimal在處理的時候把十進制小數擴大N倍讓它在整數上進行計算,並保留相應的精度資訊。至於BigDecimal是怎麼保存的可以翻閱一下原始碼。
常見問題
欄位進行學習!以上是double浮點數運算為啥會失去精確度的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 php怎麼將字串轉換成小數
Mar 22, 2023 pm 03:22 PM
php怎麼將字串轉換成小數
Mar 22, 2023 pm 03:22 PM
PHP 是一門功能強大的程式語言,廣泛應用於 Web 開發領域。其中一個非常常見的情況是需要將字串轉換為小數。這在進行資料處理的時候非常有用。在本文中,我們將介紹如何在 PHP 中將字串轉換為小數。
 PHP浮點數四捨五入法
Mar 21, 2024 am 09:21 AM
PHP浮點數四捨五入法
Mar 21, 2024 am 09:21 AM
這篇文章將為大家詳細講解有關PHP浮點數四捨五入法,小編覺得挺實用的,因此分享給大家做個參考,希望大家閱讀完這篇文章後可以有所收穫。 PHP浮點數四捨五入法概述浮點數在計算機中表示為小數點後跟指數,然而,它們通常以有限位數的近似值存儲。當需要將浮點數四捨五入到特定精度時,有幾種方法可以實現。方法1.round()函數round()函數將浮點數四捨五入為最接近的整數。它接受浮點數和可選的精度參數。例如:$num=1.55;echoround($num);//輸出:2echoround($num,1)
 使用strconv.FormatFloat函數將浮點數轉換為字串
Jul 25, 2023 am 11:45 AM
使用strconv.FormatFloat函數將浮點數轉換為字串
Jul 25, 2023 am 11:45 AM
使用strconv.FormatFloat函數將浮點數轉換為字串在Go語言中,我們經常需要將浮點數轉換為字串類型,用於輸出或儲存等需求。 Go語言中提供了strconv包,其中的FormatFloat函數可以將浮點數轉換為字串類型。 FormatFloat函數有三個參數:f表示要轉換的浮點數,fmt表示格式,以及prec表示要保留的小數位數。其中,f參數
 C++程式將double類型的變數轉換為int型別
Aug 25, 2023 pm 08:25 PM
C++程式將double類型的變數轉換為int型別
Aug 25, 2023 pm 08:25 PM
在C++中,int型別的變數只能保存正整數或負整數值;它們不能保存小數值。有float和double值可用於此目的。為了儲存小數點後最多七位的小數,創建了雙精度資料類型。整數到雙精確度資料類型的轉換可以由編譯器自動完成(稱為「隱式」轉換),也可以由程式設計師向編譯器明確要求(稱為「明確」轉換)。在接下來的部分中,我們將介紹各種轉換方法。隱式轉換編譯器會自動執行隱式類型轉換。要實現這一點,需要兩個變數——一個是浮點類型,另一個是整數類型。當我們簡單地將浮點值或變數分配給整數變數時,編譯器將處理所有其他事情
 PHP浮點數計算誤差原因及避免策略
Feb 27, 2024 pm 06:33 PM
PHP浮點數計算誤差原因及避免策略
Feb 27, 2024 pm 06:33 PM
PHP作為一種流行的伺服器端腳本語言,在進行浮點數計算時常常會遇到精確度遺失或計算誤差的問題,這些問題可能會對程式的準確性和穩定性造成影響。本文將探討PHP浮點數計算誤差的原因,並提出一些避免策略,同時給予特定的程式碼範例供參考。 1.PHP浮點數計算誤差的原因在計算機中,浮點數是以二進制形式表示的,而二進制並不能精確地表示所有的十進制小數,這就導致了浮點數的精
 深入淺出解析PHP BCMath:釋放數字運算的潛力
Feb 23, 2024 am 09:10 AM
深入淺出解析PHP BCMath:釋放數字運算的潛力
Feb 23, 2024 am 09:10 AM
:一、BCMath簡介BCMath是PHP內建的擴充庫,專門用來處理大型整數和浮點數運算。它提供了豐富的函數來進行加、減、乘、除、平方、開方等各種數學運算,並且支援多種進制的數字表示。二、BCMath的優勢BCMath相較於php原生提供的算術運算子和函數,主要有以下幾個方面的優勢:精度更高:BCMath的運算結果可以保留更多的有效數字,這對於涉及大數計算的場景尤其重要。範圍更廣:BCMath可以處理比PHP原生資料類型更大的數字,從而避免溢出或精度遺失的問題。功能更豐富:BCMath提供了
 如何在PHP中將字串轉換為浮點數
Mar 27, 2024 pm 12:48 PM
如何在PHP中將字串轉換為浮點數
Mar 27, 2024 pm 12:48 PM
將字串轉換為浮點數是在PHP中常見的操作,可以透過內建的方法來實現。首先要確保字串是合法的浮點數格式,才能成功轉換為浮點數。以下將詳細介紹如何在PHP中將字串轉換為浮點數,並提供具體的程式碼範例。一、使用(float)強制轉換在PHP中,將字串轉換為浮點數最簡單的方式就是使用強制轉換。強制轉換的方式是在字串前加上(float)即可,PHP會自動將其
 使用C#中的Math.Round函數對浮點數進行四捨五入
Nov 18, 2023 pm 02:17 PM
使用C#中的Math.Round函數對浮點數進行四捨五入
Nov 18, 2023 pm 02:17 PM
使用C#中的Math.Round函數對浮點數進行四捨五入,需要具體程式碼範例在C#程式語言中,有時我們需要對浮點數進行四捨五入操作。這時,我們可以使用Math.Round函數來實現此功能。 Math.Round函數是C#中一個用於數學計算的內建函數,其主要功能是對指定的浮點數進行四捨五入。以下是Math.Round函數的常用格式:Math.Round(doub





