一、什麼是Hash表
要想知道什麼是雜湊表，那就要先了解雜湊函數
雜湊函數:
比較先前部落格討論的二元排序樹二叉平衡樹紅黑樹B B 樹，它們的查找都是先從根節點進行查找，從節點取出資料或索引與查找值進行比較。那麼，有沒有一種函數H，根據這個函數和找出關鍵字key，可以直接決定查找值所在位置，而不需要一個個比較。這樣就**「預先知道」**key所在的位置，直接找到數據，提升效率。
即位址index=H（key）
說穿了，hash函數就是根據key計算出應該儲存位址的位置，而雜湊表是基於雜湊函數建立的一種查找表
二、雜湊函數的建構方法
根據前人經驗，統計如下幾種常用hash函數的建構方法：
直接定製法
雜湊函數為關鍵字的線性函數如H（key）=a* key b
這種建構方法比較簡便，均勻，但有很大限制，僅限於位址大小=關鍵字集合的情況
使用舉例：
假設需要統計中國人口的年齡分佈，以10為最小單元。今年是2018年，那麼10歲以內的分佈在2008-2018，20歲以內的分佈在1998-2008…假設2018代表2018-2008直接的數據，那麼關鍵字應該是2018，2008，1998…
那麼可以建構雜湊函數H（key）=（2018-key）/10=201-key/10
那麼hash表建立如下
index key 年齡 人數（假設資料）
0 2018 0-10 200W
1 2008 10-20 250W
2 1998 20-30 253W
3 1988 30- 40 300W
……
數字分析法
假設關鍵字集合中的每個關鍵字key都是由s位元數字組成（k1,k2 ,……,knk1,k2,……,kn）,分析key中的全體數據，並從中提取分佈均勻的若干位或他們的組合構成全體
使用舉例
#我們知道身分證號是有規律的，現在我們要儲存一個班級學生的身分證號碼，假設這個班級的學生都出生在同一個地區，同一年，那麼他們的身分證的前面數位都是相同的，那麼我們可以截取後面不同的幾位存儲，假設有5位元不同，那麼就用這五位來代表地址。
H（key）=key 0000
此種方法通常用於數字位數較長的情況，必須數字存在一定規律，其必須知道數字的分佈情況，如上面的例子，我們事先知道這個班級的學生出生在同一年，同一個地區。
平方取中法
如果關鍵字的每一位都有某些數字重複出現頻率很高的現象，可以先求關鍵字的平方值，透過平方擴大差異，而後取中間數字位元作為最終儲存位址。
使用範例
例如key=1234 1234^2=1522756 取227作hash位址
例如key=4321 4321^2=18671041 取671作#hash
#這個方法適合事先不知道資料且資料長度較小的情況摺疊法 如果數字的位數很多，可以將數字分割為幾個部分，取他們的疊加和作為hash位址
使用舉例
例如key=123 456 789
我們可以儲存在61524，取末三位，存在524的位置
該方法適用於數字位數較多且事先不知道資料分佈的情況
H（key）=key MOD p （p很明顯，如何選取p是個關鍵問題。
#隨機數法 H（key） =Random（ key）
取關鍵字的隨機函數值為它的雜湊位址
hash函數設計的考慮因素
1.計算雜湊位址所需的時間（即hash函數本身不要太複雜）
2.關鍵字的長度
3.表長
4.關鍵字分佈是否均勻，是否有規律可循
5.設計的hash函數在滿足以上條件的情況下盡量減少衝突
三、哈希衝突
即不同key值產生相同的位址，H（key1）=H（key2）
例如我們上面所說的儲存3 6 9，p取3是
3 MOD 3 == 6 MOD 3 == 9 MOD 3
此時3 6 9都發生了hash衝突
哈希衝突的解決方案
#不管hash函數設計的如何巧妙，總會有特殊的key導致hash衝突，特別是對動態查找表來說。
hash函數解決衝突的方法有以下常用的方法
1.開放客製化法
2.鏈結位址法
3.公共溢出區法
建立一個特殊儲存空間，專門存放衝突的資料。此種方法適用於數據和衝突較少的情況。
4.再散列法
準備若干hash函數，如果使用第一個hash函數發生了衝突，就使用第二個hash函數，第二個也衝突，使用第三個…
重點了解開放客製化法和鏈結位址法
開放客製化法
首先有一個H（key）的雜湊函數
如果H（key1）=H（keyi）
那麼keyi儲存位置Hi=(H(key) di)MODmHi=(H(key) di)MODmm為表長
注意
增量di應該具有以下特點（完整性）：產生的Hi（位址）均不相同，且所產生的s （m-1）個Hi能覆蓋hash表中的所有位址
* 平方偵測時表長m必須為4j 3的質數（平方偵測表長有限制）
#* 隨機探測時m和di沒有公因子（隨機探測di有限制）
三種開放尋址法解決衝突方案的例子
有一組資料
19 01 23 14 55 68 11 86 37要儲存在表長11的陣列中，其中H（key）=key MOD 11
那麼依照上面三種解決衝突的方法，儲存程序如下：
（表格解釋：從前向後插入數據，如果插入位置已經佔用，發生衝突，衝突的另起一行，計算地址，直到地址可用，後面衝突的繼續向下另起一行。最終結果取最上面的資料（因為是最「佔座」的資料））
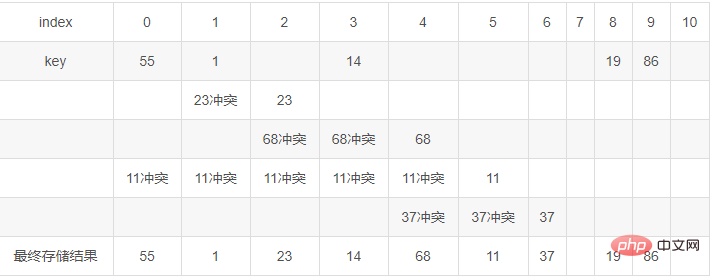
線性探測再散列
我們取di=1，即衝突後存儲在衝突後一個位置，如果仍然衝突繼續向後
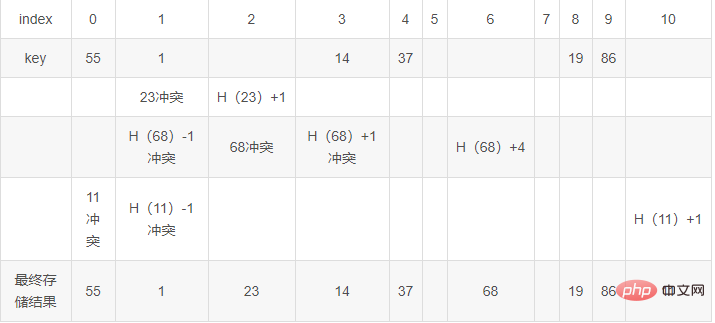
平方探測再散列
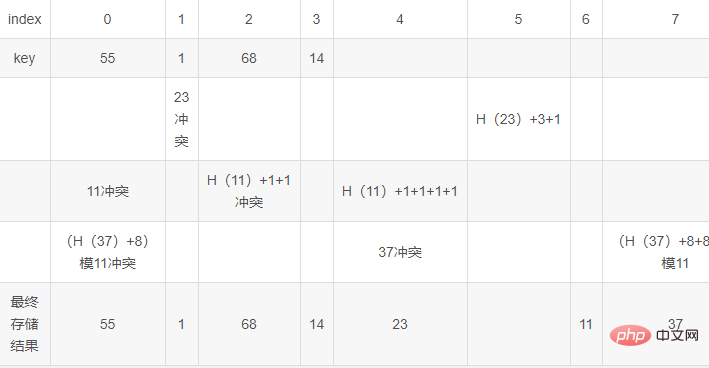
#在雜湊（雙探測再散列）
#發生衝突後
H（key）'=(H(key) di)MOD m
在此範例中
H（key）=key MOD 11
我們取di=key MOD 10 1
則有以下結果：
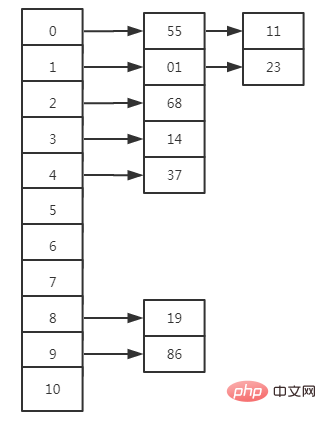
鏈結位址法
產生hash衝突後在儲存資料後面加上指針，指向後面衝突的資料
上面的例子，用鏈結位址法則是下面這樣：
四、hash表的查找
找出過程和造表過程一致，假設採用開放定址法處理衝突，則尋找過程為：
對於給定的key，計算hash位址index = H（key）
如果陣列arr【index】的值為空則尋找不成功
#如果陣列arr【index】== key 則找出成功
否則使用衝突解決方法求下一個位址，直到arr【index】== key或arr【index】==null
可以看到無論哪個函數，裝載因子越大，平均查找長度越大，那麼裝載因子α越小越好？也不是，就像100的表長只存一個數據，α是小了，但是空間利用率不高啊，這裡就是時間空間的取捨問題了。通常情況下，認為α=0.75是時間空間綜合利用效率最高的情況。
上面的這個表可是特別有用的。假設我現在有10個數據，想用鏈結位址法解決衝突，並要求平均找出長度
那麼有1 α/2
α
即n/m
m>10/2
m>5 即採用鏈結位址法，使得平均找出長度
之前我的部落格討論過各種樹的平均查找長度，他們都是基於存儲數據n的函數，而hash表不同，他是基於裝載因子的函數，也就是說，當當資料n增加時，我可以透過增加表長m，以維持裝載因子不變，確保ASL不變。
那麼hash表的建構應該是這樣的：
#五、hash表的刪除
首先鏈位址法是可以直接刪除元素的，但是開放定址法是不行的，拿前面的雙探測再散列來說，假如我們刪除了元素1，將其位置置空，那23就永遠找不到了。正確做法應該是刪除之後置入一個原來不存在的數據，例如-1。
更多相關問題請上PHP中文網：PHP實戰影片教學
#以上是什麼是資料結構Hash表（哈希表）？又有哪些具體操作呢？的詳細內容。更多資訊請關注PHP中文網其他相關文章！
