遞歸演算法的時間複雜度是：【T(n)=o(f(n))】，它表示隨問題規模n的增大，演算法的執行時間增長率和f(n)成長率成正比，稱為演算法漸進的時間複雜度。
遞迴演算法的時間複雜度
時間複雜度：
一般情況下，演算法中基本操作重複的次數就是問題規模n的某個函數f（n），進而分析f（n）隨n的變化情況並確定T（n）的數量級。這裡用‘o’來表示數量級，給出演算法時間複雜度。
T（n）=o（f（n））；
它表示隨問題規模n的增大，演算法的執行時間增長率和f（n）增長率成正比，這稱作演算法的漸進時間複雜度。而我們一般情況下討論的最壞的時間複雜度。
推薦課程：C語言教學
空間複雜度：
演算法的空間複雜度並不是實際佔用的空間，而是計算整個演算法空間輔助空間單元的個數，與問題的規模無關。演算法的空間複雜度S（n）定義為此演算法所耗費空間的數量級。
S（n）=o（f（n））
若演算法執行所需的輔助空間相對於輸入資料n而言是一個常數，則稱這個演算法空間複雜度輔助空間為o（1）；
遞迴演算法空間複雜度：遞迴深度n*每次遞迴所要的輔助空間，若每次遞迴所需的輔助空間為常數，則遞迴空間複雜度o （n）。
#遞迴演算法時間複雜度的計算方程式是一個遞歸方程式：
在引入遞歸樹之前可以考慮一個例子：
T(n) = 2T(n/2) + n2
迭代2次可以得到：
T(n) = n2 + 2(2T(n/4) + (n/2) 2)
還可以繼續迭代，將其完全展開可得：
T(n) = n2 + 2((n/2) 2 + 2((n/22)2 + 2((n/23) 2 + 2((n/24) 2 +…+2((n/2i) 2 + 2T(n/2i + 1)))…))))……(1)
而當n/2i 1 == 1時，迭代結束。
將(1)式小括號展開，可得：
T(n) = n2 + 2(n/2)2 + 22(n/22) 2 + … + 2i(n/2i)2 + 2i+1T(n/2i+1)
這恰好是一個樹狀結構，由此可引出遞歸樹法。
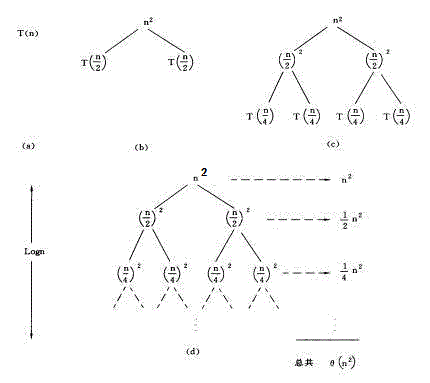
圖中的(a)(b)(c)(d)分別是遞歸樹產生的第1,2,3,n步。每一個節點中都將目前的自由項n2留在其中，而將兩個遞歸項T(n/2)
T(n/2)分別攤給了他的兩個子節點，如此循環。
圖中所有節點之和為:
[1 + 1/2 + (1/2)2 + (1/2)3 + … + (1/2)i] n2 = 2n2
可知其時間複雜度為O(n2)
可以得到遞迴樹的規則為：
(1)每層的節點為T(n) = kT(n / m) f(n)中的f(n)在目前的n/m下的值；
(2)每個節點的分支數為k；
(3)每層的右邊標示出目前層中所有節點的和。
再舉例：
T(n) = T(n/3) T(2n/3) n
其遞迴樹如下圖所示：
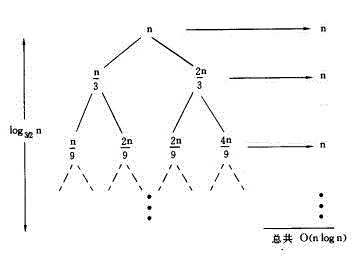
可見每層的值都為n，從根到葉節點的最長路徑是：
因為最後遞歸的停止是在(2/3)kn == 1.則
於是
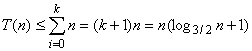
#即T(n) = O( nlogn)
總結，利用此方法解遞歸演算法複雜度：
f(n) = af(n/b) + d(n)
1.當d(n)為常數時：
# 
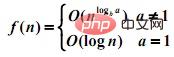
2.當d(n) = cn 時：
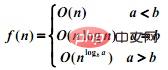
3.當d(n)為其他情況時可用遞迴樹進行分析。
由第二種情況知，若採用分治法對原演算法進行改進，則著重點是採用新的計算方法縮小a值。
以上是遞歸演算法的時間複雜度是什麼的詳細內容。更多資訊請關注PHP中文網其他相關文章！
