python排序演算法有哪些？下面本篇文章跟大家介紹一下Python十大經典排序演算法。有一定的參考價值，有需要的朋友可以參考一下，希望對大家有幫助。
現在很多的事情都可以用演算法來解決，在程式設計上，演算法有著很重要的地位，將演算法用函數封裝起來，讓程式能更好的調用，不需要反覆編寫。
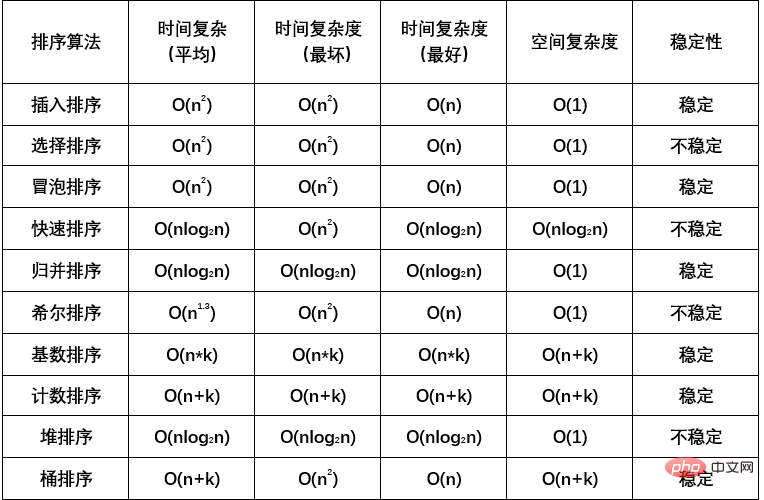
Python十大經典演算法：
一、插入排序
1.演算法想法
從第二個元素開始和前面的元素進行比較，如果前面的元素比目前元素大，則將前面元素後移，當前元素依次往前，直到找到比它小或等於它的元素插入在其後面，
然後選擇第三個元素，重複上述操作，進行插入，依次選擇到最後一個元素，插入後即完成所有排序。
2.程式碼實作
def insertion_sort(arr):
#插入排序
# 第一层for表示循环插入的遍数
for i in range(1, len(arr)):
# 设置当前需要插入的元素
current = arr[i]
# 与当前元素比较的比较元素
pre_index = i - 1
while pre_index >= 0 and arr[pre_index] > current:
# 当比较元素大于当前元素则把比较元素后移
arr[pre_index + 1] = arr[pre_index]
# 往前选择下一个比较元素
pre_index -= 1
# 当比较元素小于当前元素，则将当前元素插入在 其后面
arr[pre_index + 1] = current
return arr#二、選擇排序
1.演算法思想
設第一個元素為比較元素，依序和後面的元素比較，比較完所有元素找到最小的元素，將它和第一個元素互換，重複上述操作，我們找出第二小的元素和第二個位置的元素互換，以此類推找出剩餘最小元素將它換到前面，即完成排序。
2.程式碼實作
def selection_sort(arr):
#选择排序
# 第一层for表示循环选择的遍数
for i in range(len(arr) - 1):
# 将起始元素设为最小元素
min_index = i
# 第二层for表示最小元素和后面的元素逐个比较
for j in range(i + 1, len(arr)):
if arr[j] < arr[min_index]:
# 如果当前元素比最小元素小，则把当前元素角标记为最小元素角标
min_index = j
# 查找一遍后将最小元素与起始元素互换
arr[min_index], arr[i] = arr[i], arr[min_index]
return arr#三、冒泡排序
1 .演算法思想
從第一個和第二個開始比較，如果第一個比第二個大，則交換位置，然後比較第二個和第三個，逐漸往後，經過第一輪後最大的元素已經排在最後，
所以重複上述操作的話第二大的則會排在倒數第二的位置。 ，那重複上述操作n-1次即可完成排序，因為上一次只有一個元素所以不需要比較。
2.程式碼實作
def bubble_sort(arr):
#冒泡排序
# 第一层for表示循环的遍数
for i in range(len(arr) - 1):
# 第二层for表示具体比较哪两个元素
for j in range(len(arr) - 1 - i):
if arr[j] > arr[j + 1]:
# 如果前面的大于后面的，则交换这两个元素的位置
arr[j], arr[j + 1] = arr[j + 1], arr[j]
return arr四、快速排序
1.演算法思想
找出基準條件，這種條件必須盡可能簡單，不斷將問題分解（或縮小規模），直到符合基準條件。
2.程式碼實作
def quick_sort(arr):
if len(arr) < 2:
# 基线条件：为空或只包含一个元素的数组是“有序”的
return arr
else:
# 递归条件
pivot = arr[0]
# 由所有小于基准值的元素组成的子数组
less = [i for i in arr[1:] if i <= pivot]
# 由所有大于基准值的元素组成的子数组
greater = [i for i in array[1:] if i > pivot]
return quicksort(less) + [pivot] + quicksort(greater)
print(quick_sort([10, 5, 2, 3]))#五、歸併排序
1.演算法思想
歸併排序是分治法的典型應用。分治法（pide-and-Conquer）：將原問題劃分成n 個規模較小而結構與原問題相似的子問題；遞歸地解決這些問題，然後再合併其結果，就得到原問題的解，分解後的數列很像二元樹。
具體實作步驟：
使用遞迴將來源數列使用二分法分成多個子列
申請空間將兩個子列排序合併然後返回
將所有子列一步一步合併最後完成排序
2.程式碼實作
def merge_sort(arr):
#归并排序
if len(arr) == 1:
return arr
# 使用二分法将数列分两个
mid = len(arr) // 2
left = arr[:mid]
right = arr[mid:]
# 使用递归运算
return marge(merge_sort(left), merge_sort(right))
def marge(left, right):
#排序合并两个数列
result = []
# 两个数列都有值
while len(left) > 0 and len(right) > 0:
# 左右两个数列第一个最小放前面
if left[0] <= right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
# 只有一个数列中还有值，直接添加
result += left
result += right
return result六、希爾排序
1.演算法想法
希爾排序的整體想法是將固定間隔的幾個元素之間排序，然後再縮小這個間隔。這樣到最後數列就成為了基本有序數列。
具體步驟：
計算一個增量（間隔）值
對元素進行增量元素進行比較，例如增量值為7，那麼就對0,7,14,21…個元素進行插入排序
然後對1,8,15…進行排序，依次遞增進行排序
所有元素排序完後，縮小增量例如為3，然後重複上述第2，3步驟
最後縮小增量至1時，數列已基本有序，最後一遍普通插入即可
2.程式碼實作
def shell_sort(arr):
#希尔排序
# 取整计算增量（间隔）值
gap = len(arr) // 2
while gap > 0:
# 从增量值开始遍历比较
for i in range(gap, len(arr)):
j = i
current = arr[i]
# 元素与他同列的前面的每个元素比较，如果比前面的小则互换
while j - gap >= 0 and current < arr[j - gap]:
arr[j] = arr[j - gap]
j -= gap
arr[j] = current
# 缩小增量（间隔）值
gap //= 2
return arr#七、基數排序
1.演算法想法
基數排序（radix sort）屬於「分配式排序」（distribution sort），又稱「桶子法」（bucket sort）或bin sort，顧名思義，它是透過鍵值的部份資訊，將要排序的元素分配至某些「桶」中，藉以達到排序的作用，基數排序法是屬於穩定性的排序，其時間複雜度為O (nlog(r)m)，其中r為所採取的基數，而m為堆數，在某些時候，基數排序法的效率高於其它的穩定性排序法。
2.程式碼實作
2.1由桶排序改造，從最低位元到最高位元依序桶排序，最後輸出最後排好的清單。
def RadixSort(list,d):
for k in range(d):#d轮排序
# 每一轮生成10个列表
s=[[] for i in range(10)]#因为每一位数字都是0~9，故建立10个桶
for i in list:
# 按第k位放入到桶中
s[i//(10**k)%10].append(i)
# 按当前桶的顺序重排列表
list=[j for i in s for j in i]
return list2.2簡單實作
from random import randint
def radix_sort():
A = [randint(1, 99999999) for _ in xrange(9999)]
for k in xrange(8):
S = [ [] for _ in xrange(10)]
for j in A:
S[j / (10 ** k) % 10].append(j)
A = [a for b in S for a in b]
for i in A:
print i八、计数排序
1.算法思想
对每一个输入元素x，确定小于x的元素个数。利用这一信息，就可以直接把x 放在它在输出数组上的位置上了，运行时间为O(n)，但其需要的空间不一定，空间浪费大。
2.代码实现
from numpy.random import randint
def Conuting_Sort(A):
k = max(A) # A的最大值，用于确定C的长度
C = [0]*(k+1) # 通过下表索引，临时存放A的数据
B = (len(A))*[0] # 存放A排序完成后的数组
for i in range(0, len(A)):
C[A[i]] += 1 # 记录A有哪些数字，值为A[i]的共有几个
for i in range(1, k+1):
C[i] += C[i-1] # A中小于i的数字个数为C[i]
for i in range(len(A)-1, -1, -1):
B[C[A[i]]-1] = A[i] # C[A[i]]的值即为A[i]的值在A中的次序
C[A[i]] -= 1 # 每插入一个A[i]，则C[A[i]]减一
return B九、堆排序
1.算法思想
堆分为最大堆和最小堆，是完全二叉树。堆排序就是把堆顶的最大数取出，将剩余的堆继续调整为最大堆,具体过程在第二块有介绍，以递归实现 ，
剩余部分调整为最大堆后,再次将堆顶的最大数取出，再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束。
2.代码实现
import time,random
def sift_down(arr, node, end):
root = node
#print(root,2*root+1,end)
while True:
# 从root开始对最大堆调整
child = 2 * root +1 #left child
if child > end:
#print('break',)
break
print("v:",root,arr[root],child,arr[child])
print(arr)
# 找出两个child中交大的一个
if child + 1 <= end and arr[child] < arr[child + 1]: #如果左边小于右边
child += 1 #设置右边为大
if arr[root] < arr[child]:
# 最大堆小于较大的child, 交换顺序
tmp = arr[root]
arr[root] = arr[child]
arr[child]= tmp
# 正在调整的节点设置为root
#print("less1:", arr[root],arr[child],root,child)
root = child #
#[3, 4, 7, 8, 9, 11, 13, 15, 16, 21, 22, 29]
#print("less2:", arr[root],arr[child],root,child)
else:
# 无需调整的时候, 退出
break
#print(arr)
print('-------------')
def heap_sort(arr):
# 从最后一个有子节点的孩子还是调整最大堆
first = len(arr) // 2 -1
for i in range(first, -1, -1):
sift_down(arr, i, len(arr) - 1)
#[29, 22, 16, 9, 15, 21, 3, 13, 8, 7, 4, 11]
print('--------end---',arr)
# 将最大的放到堆的最后一个, 堆-1, 继续调整排序
for end in range(len(arr) -1, 0, -1):
arr[0], arr[end] = arr[end], arr[0]
sift_down(arr, 0, end - 1)
#print(arr)十、桶排序
1.算法思想
为了节省空间和时间，我们需要指定要排序的数据中最小以及最大的数字的值，来方便桶排序算法的运算。
2.代码实现
#桶排序
def bucket_sort(the_list):
#设置全为0的数组
all_list = [0 for i in range(100)]
last_list = []
for v in the_list:
all_list[v] = 1 if all_list[v]==0 else all_list[v]+1
for i,t_v in enumerate(all_list):
if t_v != 0:
for j in range(t_v):
last_list.append(i)
return last_list总结：
在编程中，算法都是相通的，算法重在算法思想，相当于将一道数学上的应用题的每个条件，区间，可能出现的结果进行分解，分步骤的实现它。算法就是将具体问题的共性抽象出来，将步骤用编程语言来实现。通过这次对排序算法的整理，加深了对各算法的了解，具体的代码是无法记忆的，通过对算法思想的理解，根据伪代码来实现具体算法的编程，才是真正了解算法。
推荐学习：Python视频教程
以上是python排序演算法有哪些？的詳細內容。更多資訊請關注PHP中文網其他相關文章！
