由三個結點可以構造出多少種不同的二元樹

由三個結點可以建構出5種不同的二元樹。
相關知識點介紹:
什麼是二元樹?
二元樹(Binary tree)是樹狀結構的重要型別。許多實際問題抽象化的資料結構往往是二元樹形式,即使是一般的樹也能簡單地轉換為二元樹,而且二元樹的儲存結構及其演算法都較為簡單,因此二元樹顯得特別重要。
二元樹特徵:
每個結點最多只能有兩棵子樹,且有左右之分。
二元樹是n個有限元素的集合,該集合或為空、或由一個稱為根(root)的元素及兩個不相交的、被分別稱為左子樹和右子樹的二元樹組成,是有序樹。當集合為空時,稱該二元樹為空二元樹。在二元樹中,一個元素也稱為一個結點。
以上是由三個結點可以構造出多少種不同的二元樹的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 CentOS7系統安裝與設定 DRBD?實現高可用性和資料冗餘教程!
Feb 22, 2024 pm 02:13 PM
CentOS7系統安裝與設定 DRBD?實現高可用性和資料冗餘教程!
Feb 22, 2024 pm 02:13 PM
DRBD(DistributedReplicatedBlockDevice)是一種用於實現資料冗餘和高可用性的開源解決方案。以下是在CentOS7系統上安裝和設定DRBD的教學:安裝DRBD:開啟終端機並以管理員身分登入CentOS7系統。執行以下命令以安裝DRBD軟體包:sudoyuminstalldrbd配置DRBD:編輯DRBD設定檔(通常位於/etc/drbd.d目錄下),配置DRBD資源的設定。例如,可以定義主節點和備份節點的IP位址、連接埠和設備等。確保主節點和備份節點之間可以透過網
 節點從Proxmox VE徹底撤離及再次加入集群
Feb 21, 2024 pm 12:40 PM
節點從Proxmox VE徹底撤離及再次加入集群
Feb 21, 2024 pm 12:40 PM
節點從ProxmoxVE徹底撤離及再次加入叢集場景描述當ProxmoxVE叢集中有節點損壞無法快速修復時,需要將故障節點乾淨的從叢集踢出,並把殘留資訊清理乾淨。否則,新的節點用故障節點曾使用用的IP的位址將無法正常加入叢集;同樣,從叢集中脫離出來的故障節點修復後,雖然與叢集已經毫無關係,但存取此單節點的Web管理後台,將出現原ProxmoxVE叢集其它節點的訊息,非常惱火。從集群中驅逐節點如果ProxmoxVE是Ceph超融合集群,則需要登入集群任意節點(欲刪除節點除外)宿主系統Debian,命令
 教你如何搭建K8S集群。
Feb 18, 2024 pm 05:00 PM
教你如何搭建K8S集群。
Feb 18, 2024 pm 05:00 PM
建置Kubernetes(K8S)叢集通常涉及多個步驟和元件配置。以下是一個簡要的搭建Kubernetes叢集的指南:準備環境:至少兩台運行Linux作業系統的伺服器節點,這些節點將用於搭建叢集。這些節點可以是實體伺服器或虛擬機器。確保所有節點之間的網路連通性,並且它們可以相互存取。安裝Docker:在每個節點上安裝Docker,以便能夠在節點上運行容器。可以根據不同的Linux發行版使用對應的套件管理工具(如apt、yum)安裝Docker。安裝Kubernetes元件:在每個節點上安裝Kuber
 在C語言中列印二元樹的左視圖
Sep 03, 2023 pm 01:25 PM
在C語言中列印二元樹的左視圖
Sep 03, 2023 pm 01:25 PM
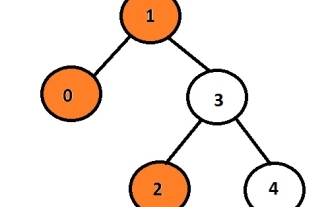
任務是列印給定二元樹的左節點。首先,使用者將插入數據,從而生成二元樹,然後列印所形成的樹的左側視圖。每個節點最多可以有2個子節點,因此這裡程式必須僅遍歷與節點關聯的左指針如果左指針不為空,則表示它將有一些與之關聯的資料或指針,否則它將是要列印並顯示為輸出的左子級。範例Input:10324Output:102這裡,橘色節點代表二元樹的左邊視圖。在給定的圖中,資料為1的節點是根節點,因此它將被列印,而不是轉到左子節點,它將列印0,然後它將轉到3並列印其左子節點,即2 。我們可以使用遞歸方法來儲存節點的級
 Java中的二元樹結構詳解
Jun 16, 2023 am 08:58 AM
Java中的二元樹結構詳解
Jun 16, 2023 am 08:58 AM
二元樹是計算機科學中常見的資料結構,也是Java程式設計中常用的資料結構。本文將詳細介紹Java中的二元樹結構。一、什麼是二元樹?在電腦科學中,二元樹是一種樹狀結構,每個節點最多有兩個子節點。其中,左側子節點比父節點小,右側子節點比父節點大。在Java程式設計中,常用二元樹表示排序,搜尋以及提高對資料的查詢效率。二、Java中的二元樹實作在Java中,二元樹
 在C語言中,將二元樹的右側視圖列印出來
Sep 16, 2023 pm 11:13 PM
在C語言中,將二元樹的右側視圖列印出來
Sep 16, 2023 pm 11:13 PM
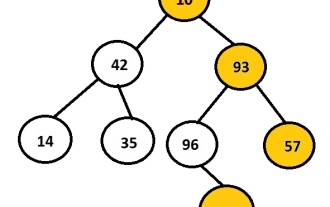
任務是列印給定二元樹的右節點。首先使用者將插入資料以建立二元樹,然後列印所形成的樹的右視圖。上圖展示了使用節點10、42、93、14、35、96、57和88建立的二元樹,其中選擇並顯示在樹的右側的節點。例如,10、93、57和88是二元樹的最右節點。範例Input:1042931435965788Output:10935788每個節點都有兩個指針,即左指針和右指針。根據這個問題,程式只需遍歷右節點。因此,不需要考慮節點的左子節點。右視圖儲存了所有那些是其所在層級的最後一個節點的節點。因此,我們可以
 如何使用Python實作二元樹的遍歷
Jun 09, 2023 pm 09:12 PM
如何使用Python實作二元樹的遍歷
Jun 09, 2023 pm 09:12 PM
作為一種常用的資料結構,二元樹經常被用來儲存資料、搜尋和排序。遍歷二元樹是非常常見的操作之一。 Python作為一種簡單易用的程式語言,有許多方法可以實作二元樹的遍歷。本文將介紹如何使用Python實現二元樹的前序、中序和後序遍歷。二元樹的基礎在學習二元樹的遍歷之前,我們需要先了解二元樹的基本概念。二元樹由節點組成,每個節點都有一個值和兩個子節點(左子節點和右子
 二元樹中等腰三角形的數量
Sep 05, 2023 am 09:41 AM
二元樹中等腰三角形的數量
Sep 05, 2023 am 09:41 AM
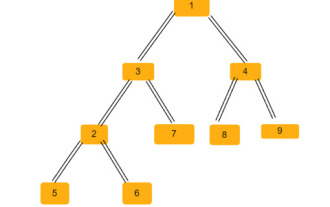
二元樹是一種資料結構,其中每個節點最多可以有兩個子節點。這些孩子分別稱為左孩子和右孩子。假設我們得到了一個父數組表示,您必須使用它來建立一棵二元樹。二元樹可能有幾個等腰三角形。我們必須找到該二元樹中可能的等腰三角形的總數。在本文中,我們將探討幾種在C++中解決這個問題的技術。理解問題給你一個父數組。您必須以二元樹的形式表示它,以便數組索引形成樹節點的值,而數組中的值給出該特定索引的父節點。請注意,-1始終是根父節點。下面給出的是一個數組及其二元樹表示。 Parentarray=[0,-1,3,1,





