圖的廣度優先遍歷類似二元樹的什麼?
圖的廣度優先遍歷即橫向優先遍歷,類似二元樹的按層遍歷。廣度優先遍歷是從根結點開始沿著樹的寬度搜尋遍歷,即按層次的去遍歷;從上往下對每一層依次訪問,在每層中,從左往右(或右往左)訪問結點,訪問完一層就進入下一層,直到沒有結點可以訪問為止。

1.前言
和樹的遍歷類似,圖的遍歷也是從圖中某點出發,然後按照某種方法對圖中所有頂點進行訪問,且僅訪問一次。
但是圖的遍歷相對樹而言要更為複雜。因為圖中的任一頂點都可能與其他頂點相鄰,所以在圖的遍歷中必須記錄已被造訪的頂點,避免重複造訪。
根據搜尋路徑的不同,我們可以將遍歷圖的方法分為兩種:廣度優先搜尋和深度優先搜尋。
2.圖的基本概念
2.1.無向圖和無向圖
頂點對(u,v)是無序的,即(u,v )和(v,u)是同一條邊。常用一對圓括號表示。
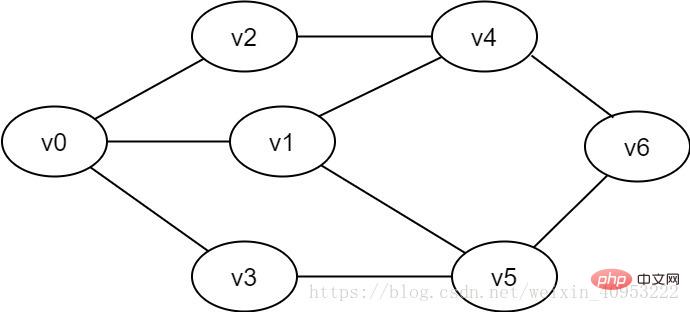
圖2-1-1 無向圖範例
頂點對
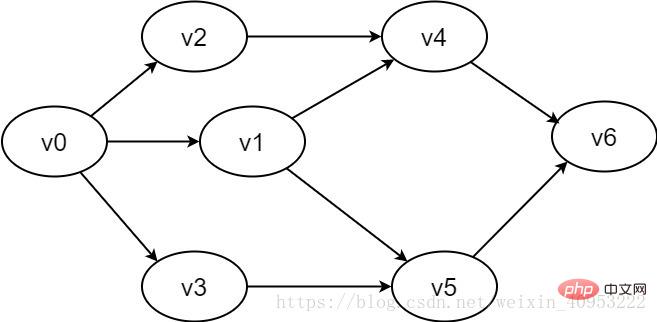
圖2-1-2 有向圖範例
2.2 .權和網
圖的每條邊上可能存在具有某種意義的數值,稱該數值為該邊上的權。而這種帶權的圖稱為網。
2.3.連通圖與非連通圖
連通圖:在無向圖G中,從頂點v到頂點v'有路徑,則稱v和v'是聯通的。若圖中任兩頂點v、v'∈V,v和v'之間均聯通,則稱G為連通圖。上述兩圖均為連通圖。
非連通圖:若無向圖G中,存在v和v'之間不連通,則稱G為非連通圖。
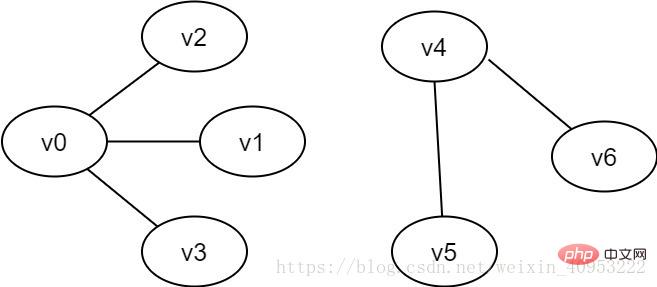
圖2-3 非連通圖範例
3.廣度優先搜尋
3.1.演算法的基本想法
廣度優先搜尋類似樹的層次遍歷過程。它需要藉助一個佇列來實作。如圖2-1-1所示,要遍歷從v0到v6的每一個頂點,我們可以設v0為第一層,v1、v2、v3為第二層,v4、v5為第三層,v6為第四層,再逐一遍歷每一層的每個頂點。
具體過程如下:
1.準備工作:建立一個visited數組,用來記錄已被訪問過的頂點;建立一個佇列,用來存放每一層的頂點;初始化圖G。
2.從圖中的v0開始訪問,將的visited[v0]陣列的值設為true,同時將v0入隊。
3.只要隊列不空,則重複如下:
(1)隊頭頂點u出隊。
(2)依序檢查u的所有鄰接頂點w,若visited[w]的值為false,則造訪w,並將visited[w]置為true,同時將w入隊。
3.2.演算法的實作過程
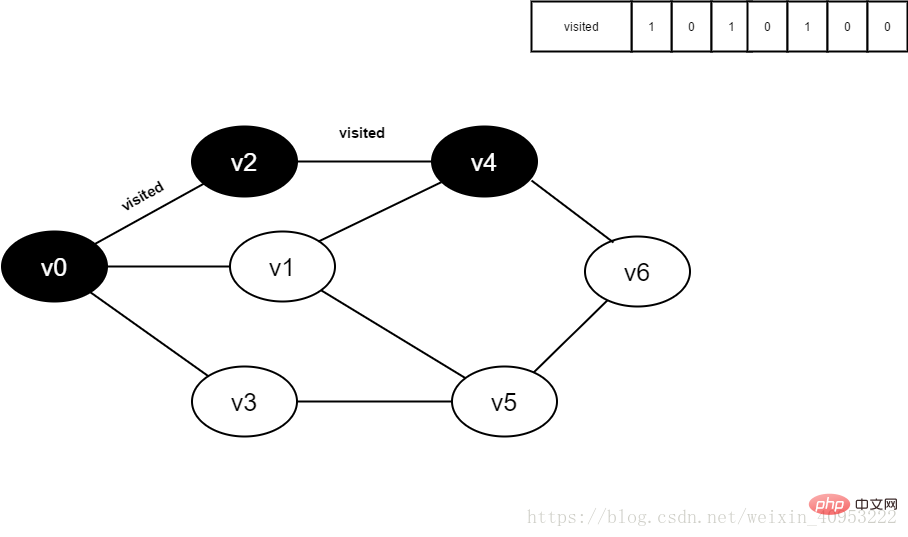
白色表示未被訪問,灰色表示即將訪問,黑色表示已訪問。
visited陣列:0表示未訪問,1表示以訪問。
佇列:隊頭出元素,隊尾進元素。
1.初始時全部頂點皆未被訪問,visited陣列初始化為0,佇列中沒有元素。
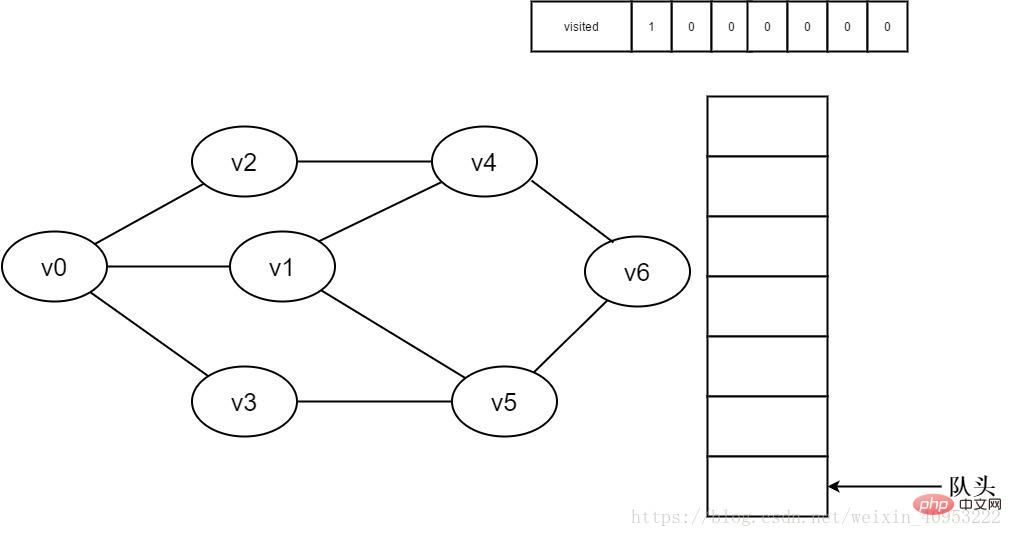
圖3-2-1
2.即將造訪頂點v0。
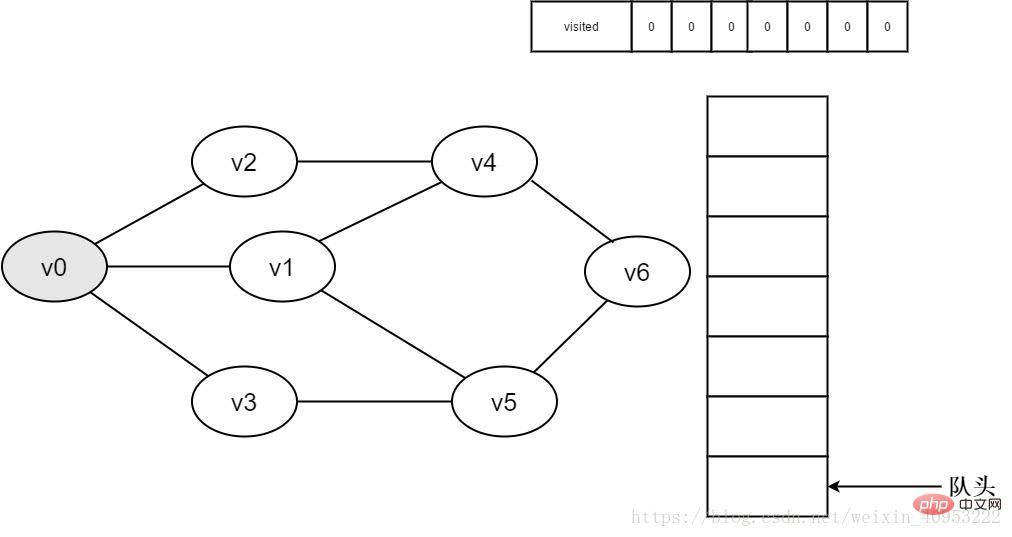
#圖3-2-2
3.存取頂點v0,並置visited[0 ]的值為1,同時將v0入隊。
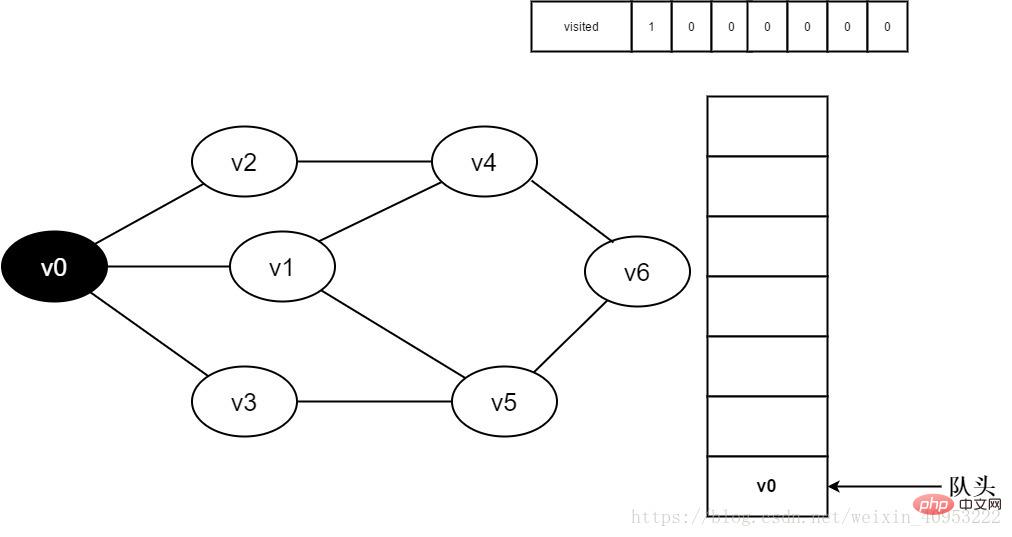
#圖3-2-3
4.將v0出隊,訪問v0的鄰接點v2。判斷visited[2],因為visited[2]的值為0,訪問v2。
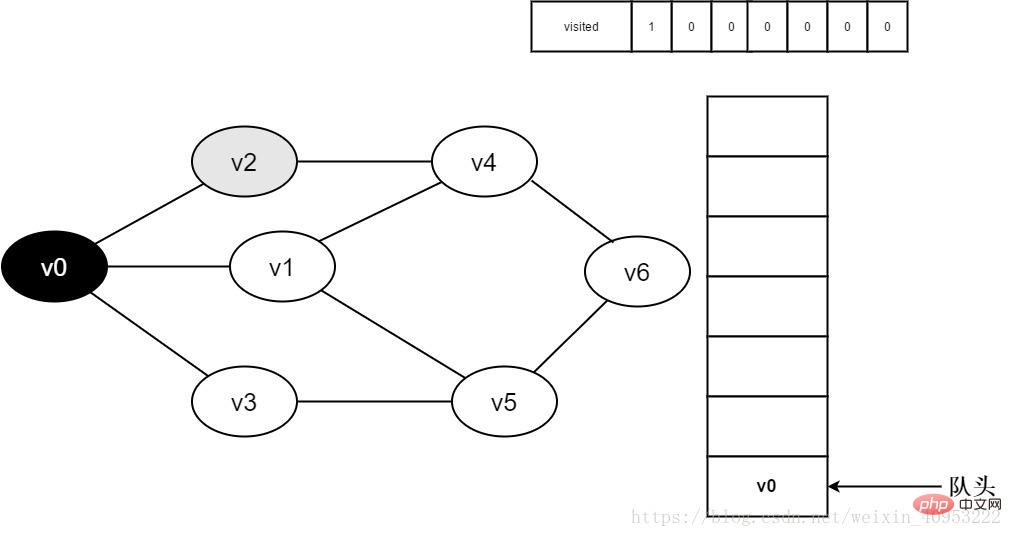
圖3-2-4
#5.將visited[2]置為1,並將v2入隊。
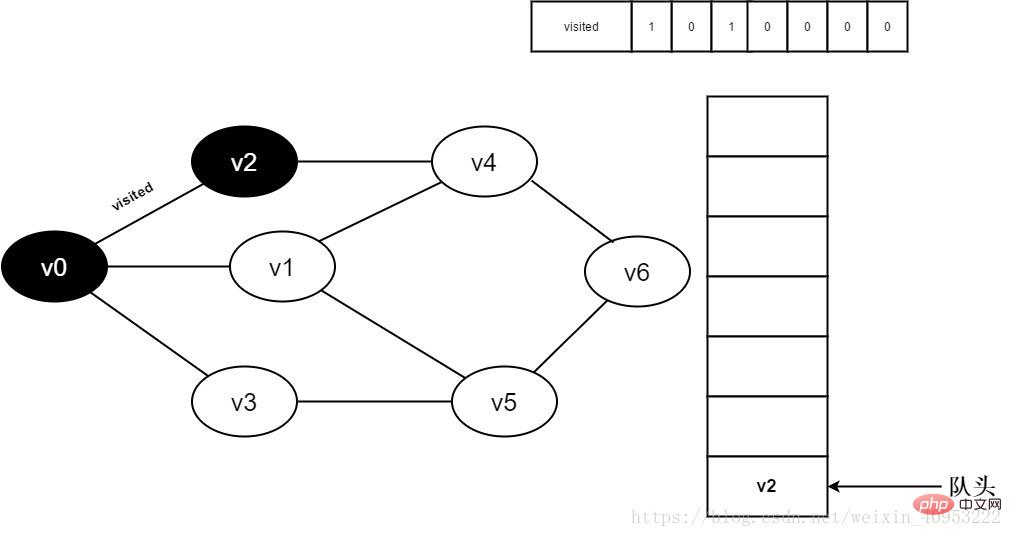
圖3-2-5
#6.訪問v0鄰接點v1。判斷visited[1],因為visited[1]的值為0,訪問v1。
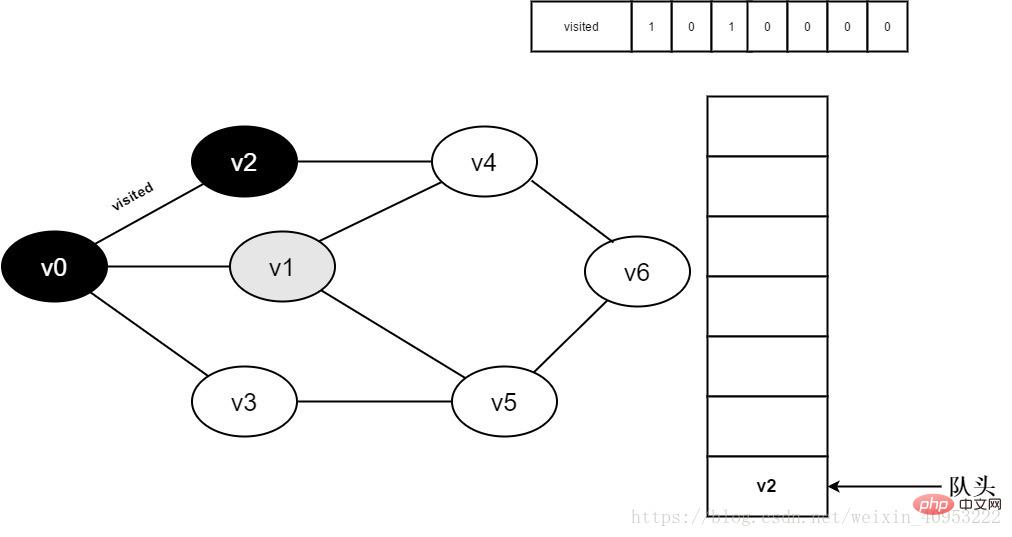
圖3-2-6
#7.將visited[1]置為0,並將v1入隊。
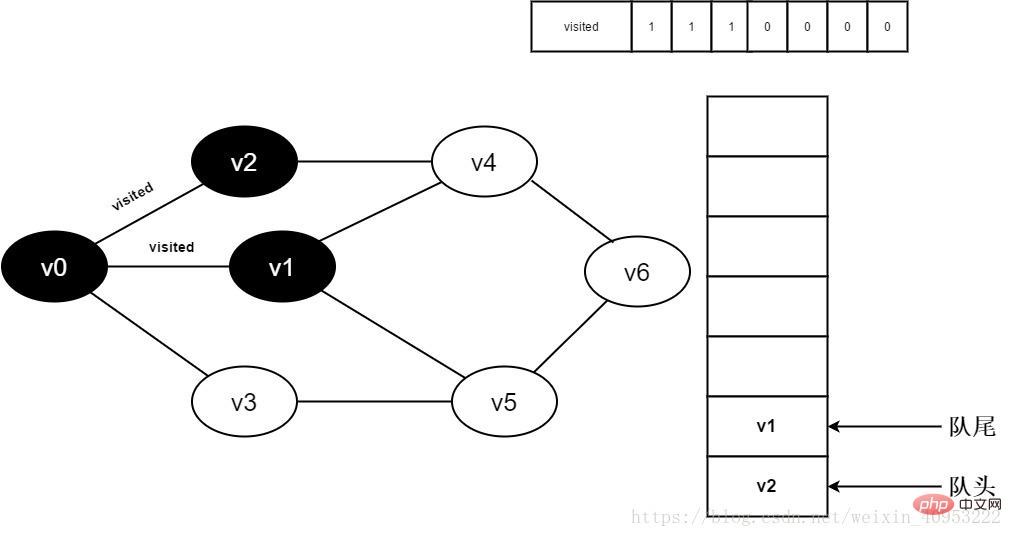
圖3-2-7
#8.判斷visited[3],因為它的值為0 ,訪問v3。將visited[3]置為0,將v3入隊。
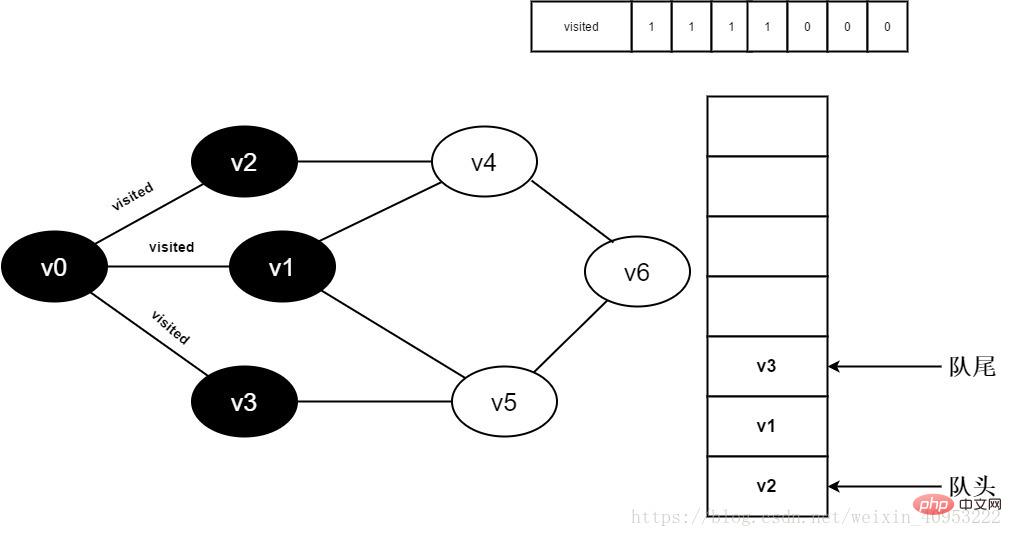
圖3-2-8
#9.v0的全部鄰接點都已被存取完成。將隊頭元素v2出隊,開始造訪v2的所有鄰接點。
開始訪問v2鄰接點v0,判斷visited[0],因為其值為1,不進行訪問。
繼續存取v2鄰接點v4,判斷visited[4],因為其值為0,存取v4,如下圖:
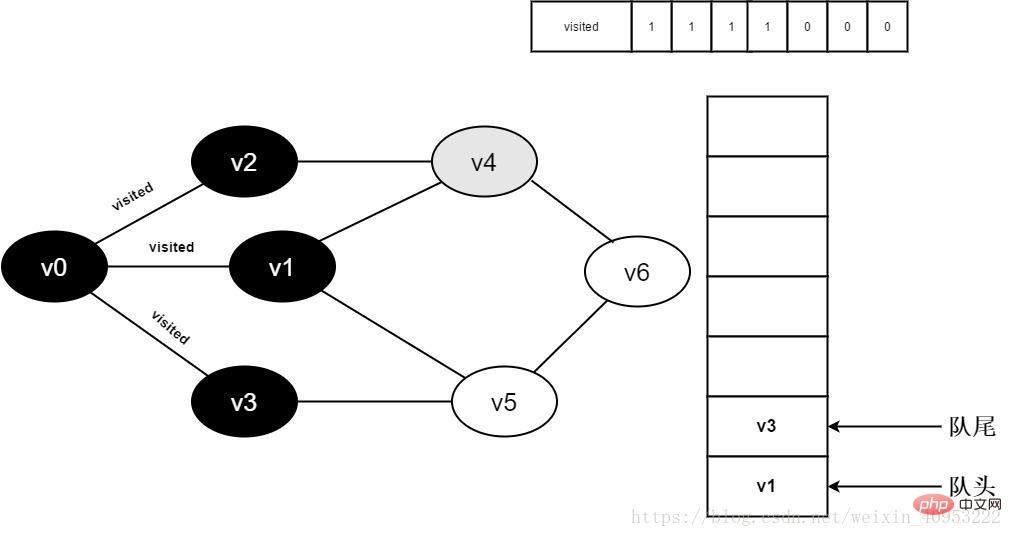
圖3-2-9
10.將visited[4]置為1,將v4入隊。

圖3-2-10
#11.v2的全部鄰接點都已被存取完成。將隊頭元素v1出隊,開始造訪v1的所有鄰接點。
開始訪問v1鄰接點v0,因為visited[0]值為1,不進行訪問。
繼續訪問v1鄰接點v4,因為visited[4]的值為1,不進行訪問。
繼續訪問v1鄰接點v5,因為visited[5]值為0,訪問v5,如下圖:

圖3-2-11
12.將visited[5]置為1,並將v5入隊。
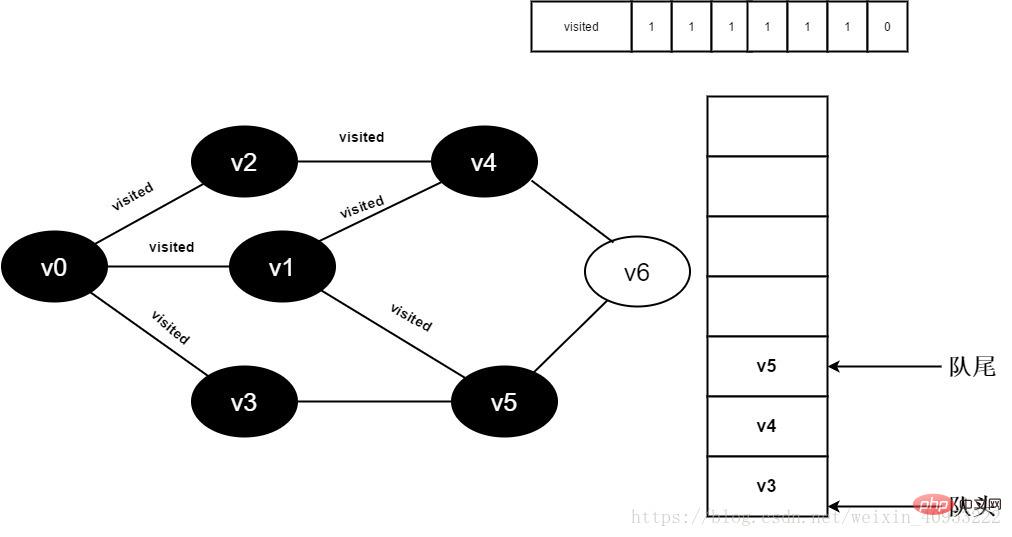
圖3-2-12
#13.v1的全部鄰接點都已被訪問完畢,將隊頭元素v3出隊,開始造訪v3的所有鄰接點。
開始訪問v3鄰接點v0,因為visited[0]值為1,不進行訪問。
繼續訪問v3鄰接點v5,因為visited[5]值為1,不進行訪問。
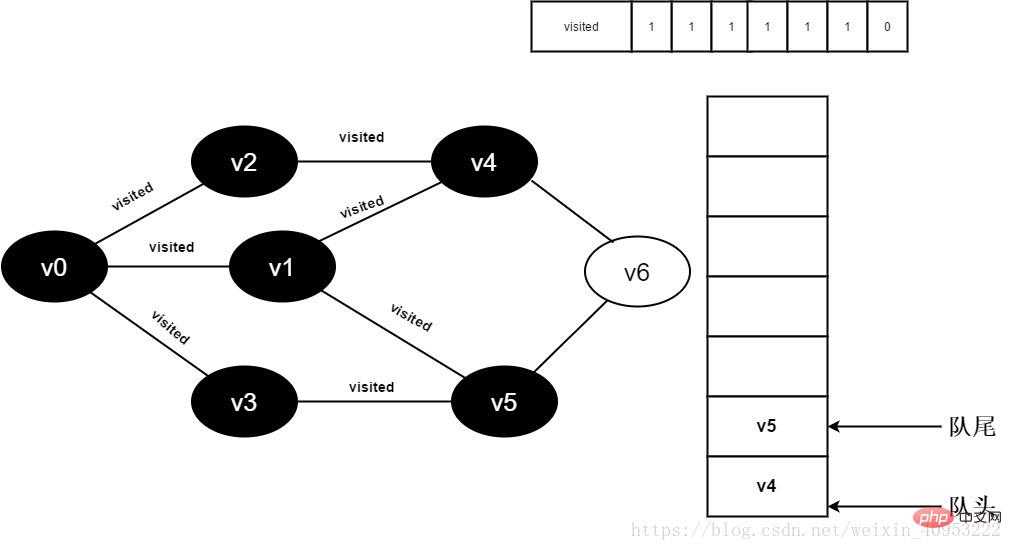
圖3-2-13
#14.v3的全部鄰接點都已被存取完畢,將隊頭元素v4出隊,開始造訪v4的所有鄰接點。
開始訪問v4的鄰接點v2,因為visited[2]的值為1,不進行訪問。
繼續訪問v4的鄰接點v6,因為visited[6]的值為0,訪問v6,如下圖:
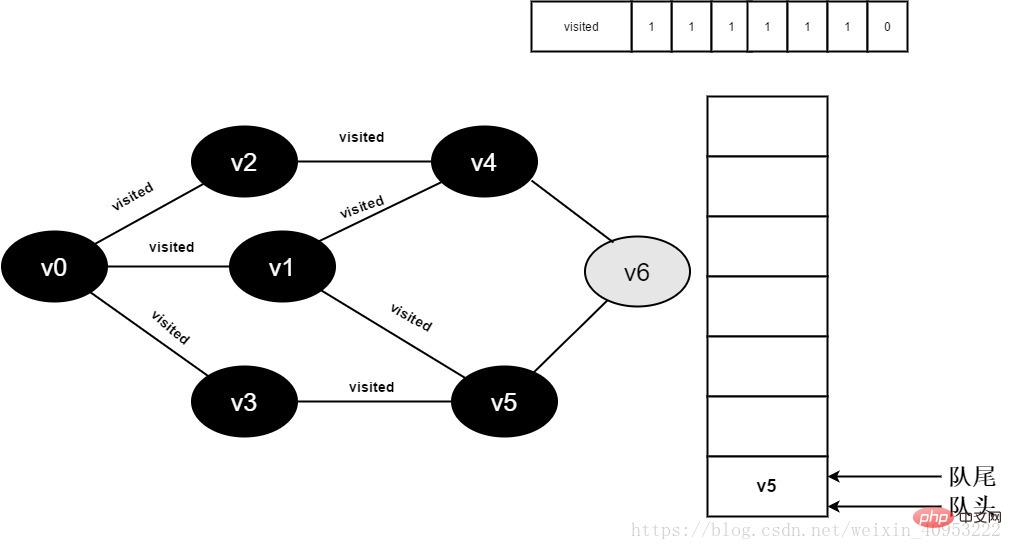
圖3-2-14
15.將visited[6]值為1,並將v6入隊。
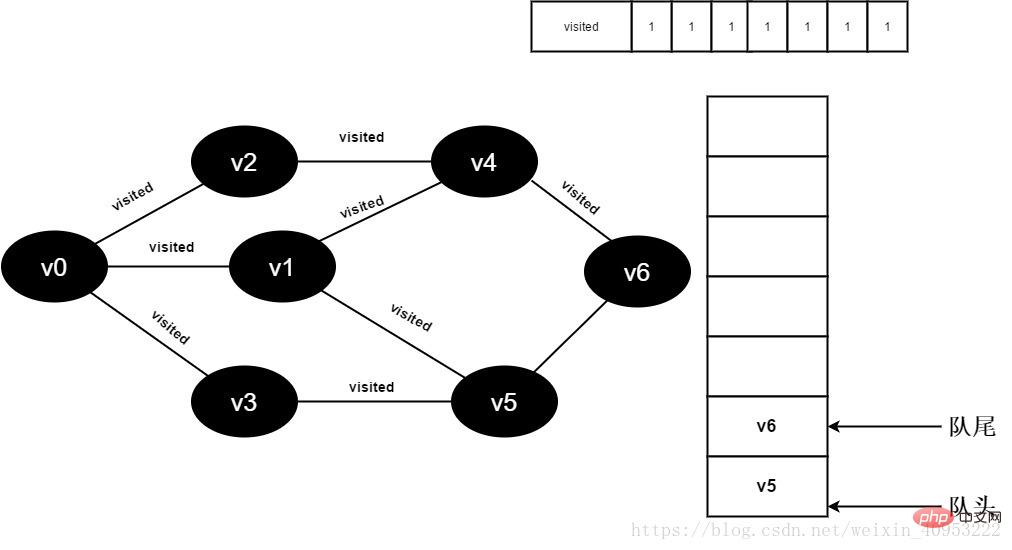
圖3-2-15
#16.v4的全部鄰接點都已被存取完畢,將隊頭元素v5出隊,開始造訪v5的所有鄰接點。
開始訪問v5鄰接點v3,因為visited[3]的值為1,不進行訪問。
繼續訪問v5鄰接點v6,因為visited[6]的值為1,不進行訪問。
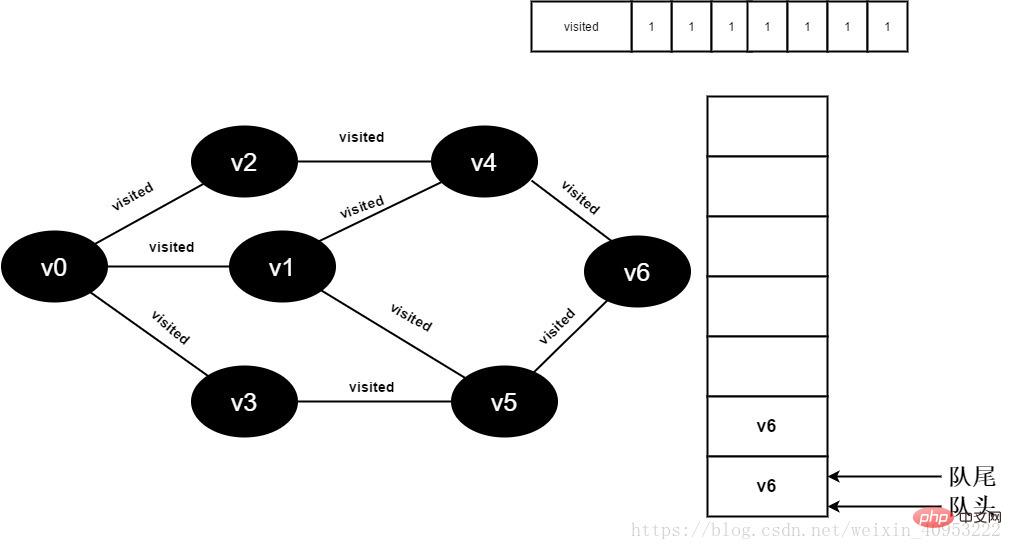
圖3-2-16
#17.v5的全部鄰接點都已被存取完畢,將隊頭元素v6出隊,開始造訪v6的所有鄰接點。
開始訪問v6鄰接點v4,因為visited[4]的值為1,不進行訪問。
繼續訪問v6鄰接點v5,因為visited[5]的值文1,不進行訪問。
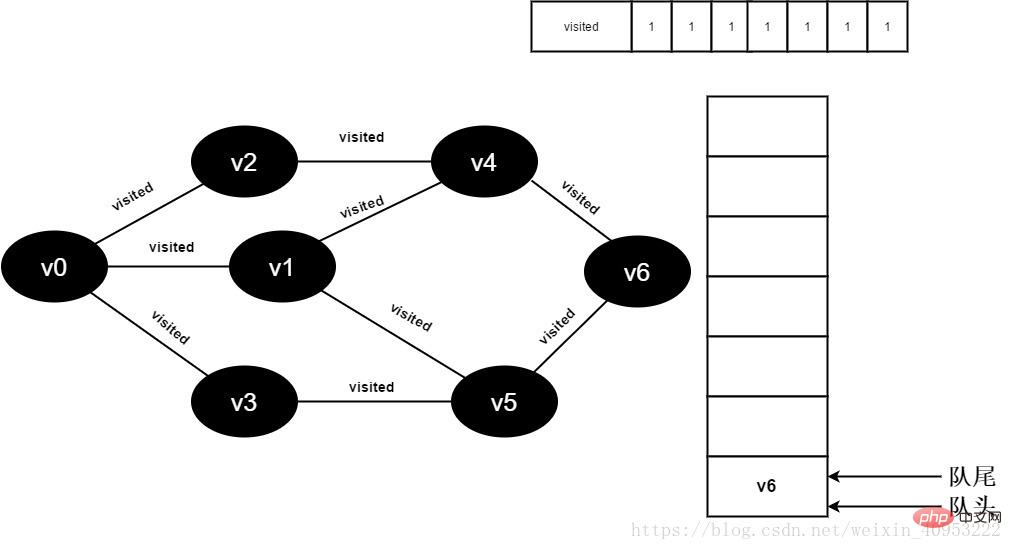
圖3-2-17
#18.佇列為空,退出循環,全部頂點都存取完畢。

#圖3-2-18
3.3具體程式碼的實作
3.3.1用鄰接矩陣表示圖的廣度優先搜尋
/*一些量的定义*/ queue<char> q; //定义一个队列,使用库函数queue #define MVNum 100 //表示最大顶点个数 bool visited[MVNum]; //定义一个visited数组,记录已被访问的顶点
/*邻接矩阵存储表示*/
typedef struct AMGraph
{
char vexs[MVNum]; //顶点表
int arcs[MVNum][MVNum]; //邻接矩阵
int vexnum, arcnum; //当前的顶点数和边数
}
AMGraph;/*找到顶点v的对应下标*/
int LocateVex(AMGraph &G, char v)
{
int i;
for (i = 0; i < G.vexnum; i++)
if (G.vexs[i] == v)
return i;
}/*采用邻接矩阵表示法,创建无向图G*/
int CreateUDG_1(AMGraph &G)
{
int i, j, k;
char v1, v2;
scanf("%d%d", &G.vexnum, &G.arcnum); //输入总顶点数,总边数
getchar(); //获取'\n’,防止其对之后的字符输入造成影响
for (i = 0; i < G.vexnum; i++)
scanf("%c", &G.vexs[i]); //依次输入点的信息
for (i = 0; i < G.vexnum; i++)
for (j = 0; j < G.vexnum; j++)
G.arcs[i][j] = 0; //初始化邻接矩阵边,0表示顶点i和j之间无边
for (k = 0; k < G.arcnum; k++)
{
getchar();
scanf("%c%c", &v1, &v2); //输入一条边依附的顶点
i = LocateVex(G, v1); //找到顶点i的下标
j = LocateVex(G, v2); //找到顶点j的下标
G.arcs[i][j] = G.arcs[j][i] = 1; //1表示顶点i和j之间有边,无向图不区分方向
}
return 1;
}/*采用邻接矩阵表示图的广度优先遍历*/
void BFS_AM(AMGraph &G,char v0)
{
/*从v0元素开始访问图*/
int u,i,v,w;
v = LocateVex(G,v0); //找到v0对应的下标
printf("%c ", v0); //打印v0
visited[v] = 1; //顶点v0已被访问
q.push(v0); //将v0入队
while (!q.empty())
{
u = q.front(); //将队头元素u出队,开始访问u的所有邻接点
v = LocateVex(G, u); //得到顶点u的对应下标
q.pop(); //将顶点u出队
for (i = 0; i < G.vexnum; i++)
{
w = G.vexs[i];
if (G.arcs[v][i] && !visited[i])//顶点u和w间有边,且顶点w未被访问
{
printf("%c ", w); //打印顶点w
q.push(w); //将顶点w入队
visited[i] = 1; //顶点w已被访问
}
}
}
}3.3.2用鄰接表表示圖的廣度優先搜尋
/*找到顶点对应的下标*/
int LocateVex(ALGraph &G, char v)
{
int i;
for (i = 0; i < G.vexnum; i++)
if (v == G.vertices[i].data)
return i;
}/*邻接表存储表示*/
typedef struct ArcNode //边结点
{
int adjvex; //该边所指向的顶点的位置
ArcNode *nextarc; //指向下一条边的指针
int info; //和边相关的信息,如权值
}ArcNode;
typedef struct VexNode //表头结点
{
char data;
ArcNode *firstarc; //指向第一条依附该顶点的边的指针
}VexNode,AdjList[MVNum]; //AbjList表示一个表头结点表
typedef struct ALGraph
{
AdjList vertices;
int vexnum, arcnum;
}ALGraph;/*采用邻接表表示法,创建无向图G*/
int CreateUDG_2(ALGraph &G)
{
int i, j, k;
char v1, v2;
scanf("%d%d", &G.vexnum, &G.arcnum); //输入总顶点数,总边数
getchar();
for (i = 0; i < G.vexnum; i++) //输入各顶点,构造表头结点表
{
scanf("%c", &G.vertices[i].data); //输入顶点值
G.vertices[i].firstarc = NULL; //初始化每个表头结点的指针域为NULL
}
for (k = 0; k < G.arcnum; k++) //输入各边,构造邻接表
{
getchar();
scanf("%c%c", &v1, &v2); //输入一条边依附的两个顶点
i = LocateVex(G, v1); //找到顶点i的下标
j = LocateVex(G, v2); //找到顶点j的下标
ArcNode *p1 = new ArcNode; //创建一个边结点*p1
p1->adjvex = j; //其邻接点域为j
p1->nextarc = G.vertices[i].firstarc; G.vertices[i].firstarc = p1; // 将新结点*p插入到顶点v1的边表头部
ArcNode *p2 = new ArcNode; //生成另一个对称的新的表结点*p2
p2->adjvex = i;
p2->nextarc = G.vertices[j].firstarc;
G.vertices[j].firstarc = p1;
}
return 1;
}/*采用邻接表表示图的广度优先遍历*/
void BFS_AL(ALGraph &G, char v0)
{
int u,w,v;
ArcNode *p;
printf("%c ", v0); //打印顶点v0
v = LocateVex(G, v0); //找到v0对应的下标
visited[v] = 1; //顶点v0已被访问
q.push(v0); //将顶点v0入队
while (!q.empty())
{
u = q.front(); //将顶点元素u出队,开始访问u的所有邻接点
v = LocateVex(G, u); //得到顶点u的对应下标
q.pop(); //将顶点u出队
for (p = G.vertices[v].firstarc; p; p = p->nextarc) //遍历顶点u的邻接点
{
w = p->adjvex;
if (!visited[w]) //顶点p未被访问
{
printf("%c ", G.vertices[w].data); //打印顶点p
visited[w] = 1; //顶点p已被访问
q.push(G.vertices[w].data); //将顶点p入队
}
}
}
}#3.4.非聯通圖的廣度優先遍歷的實現方法
/*广度优先搜索非连通图*/
void BFSTraverse(AMGraph G)
{
int v;
for (v = 0; v < G.vexnum; v++)
visited[v] = 0; //将visited数组初始化
for (v = 0; v < G.vexnum; v++)
if (!visited[v]) BFS_AM(G, G.vexs[v]); //对尚未访问的顶点调用BFS
}4.深度優先搜尋
4.1演算法的基本想法
深度優先搜尋類似於樹的先序遍歷,具體流程如下:
準備工作:建立一個visited數組,用來記錄所有被造訪過的頂點。
1.從圖中v0出發,訪問v0。
2.找出v0的第一個未被訪問的鄰接點,訪問該頂點。以此頂點為新頂點,重複此步驟,直到剛造訪過的頂點沒有未被造訪的鄰接點為止。
3.返回前一個訪問過的仍有未被訪問鄰接點的頂點,繼續訪問該頂點的下一個未被訪問領接點。
4.重複2,3步驟,直至所有頂點均被訪問,搜尋結束。
4.2演算法的實作過程
1.初始時所有頂點均未被訪問,visited陣列為空。

圖4-2-1
#2.即將造訪v0。

圖4-2-2
#3.存取v0,並將visited[0]的值置為1。
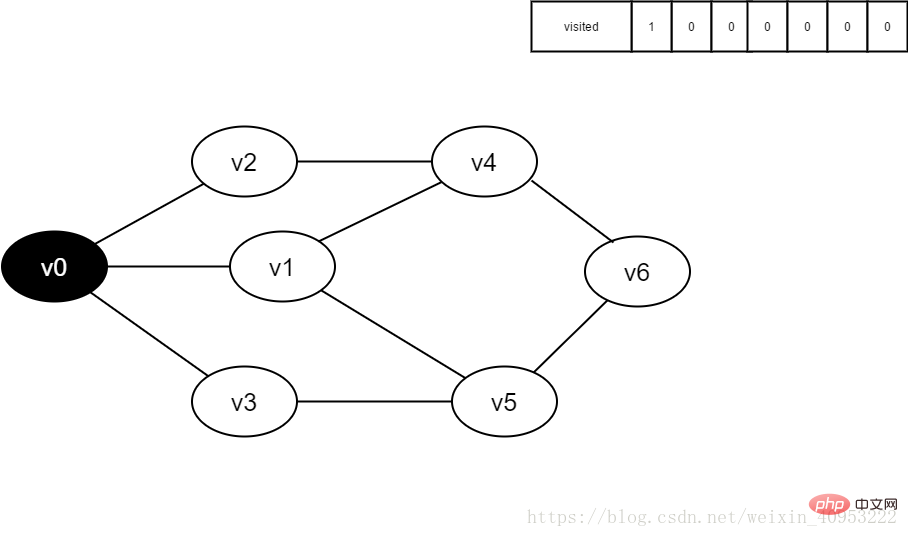
圖4-2-3
#4.訪問v0的鄰接點v2,判斷visited [2],因其值為0,訪問v2。
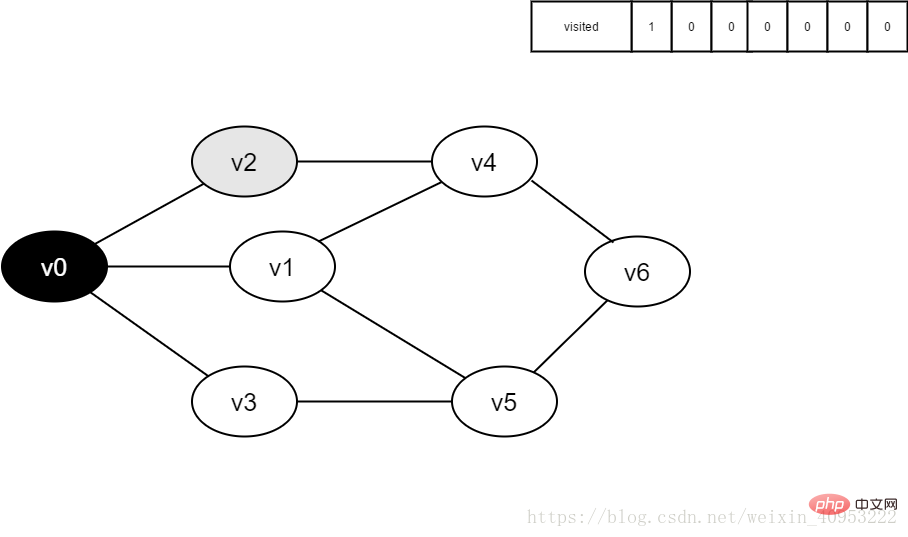
圖4-2-4
#5.將visited[2]設為1。
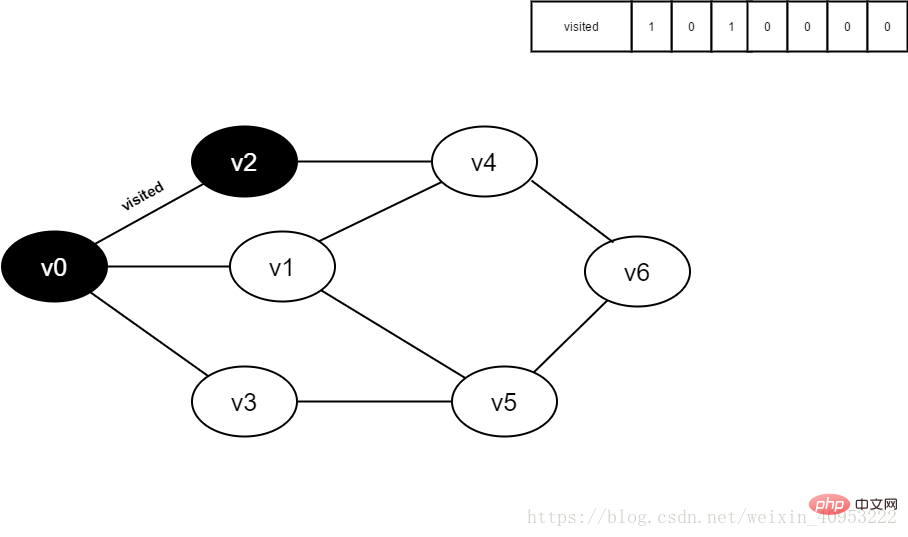
圖4-2-5
#6.訪問v2的鄰接點v0,判斷visited [0],其值為1,不訪問。
繼續訪問v2的鄰接點v4,判斷visited[4],其值為0,訪問v4。
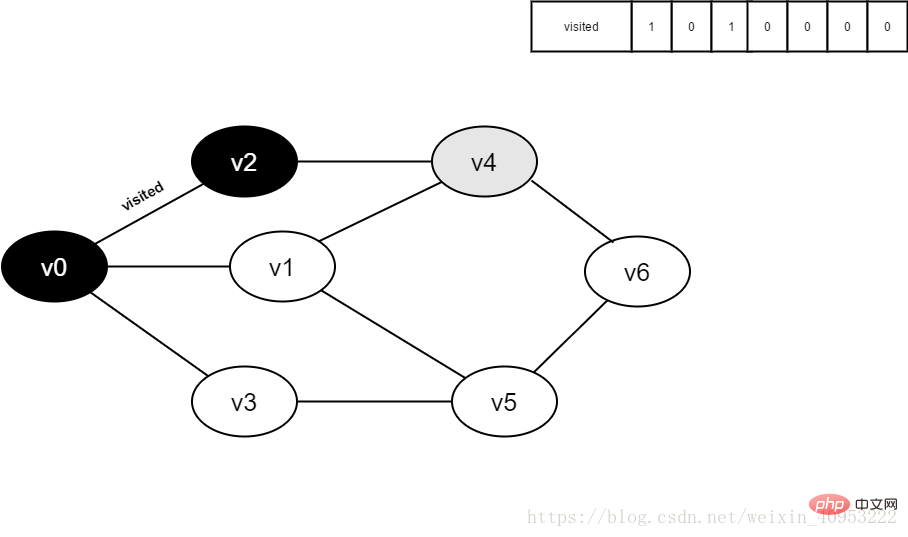
圖4-2-6
#7.將visited[4]設為1。
圖4-2-7
#8.訪問v4的鄰接點v1,判斷visited[1],其值為0,訪問v1。
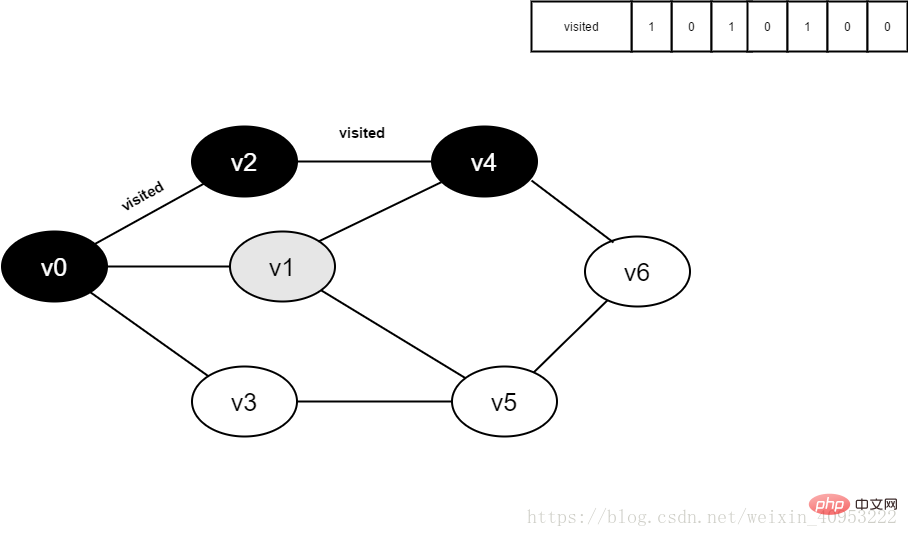
圖4-2-8
#9.將visited[1]設為1。
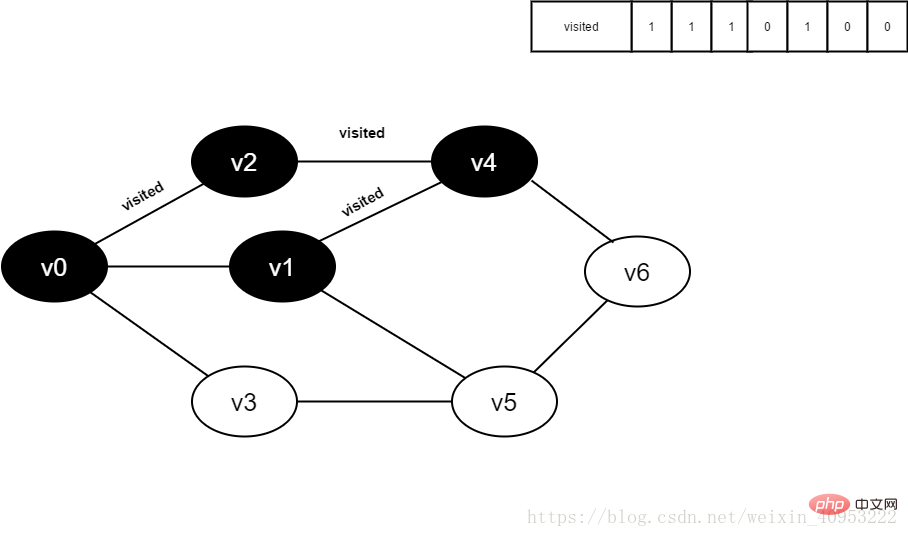
圖4-2-9
#10.訪問v1的鄰接點v0,判斷visited [0],其值為1,不訪問。
繼續訪問v1的鄰接點v4,判斷visited[4],其值為1,不訪問。
繼續存取v1的鄰接點v5,判讀visited[5],其值為0,存取v5。
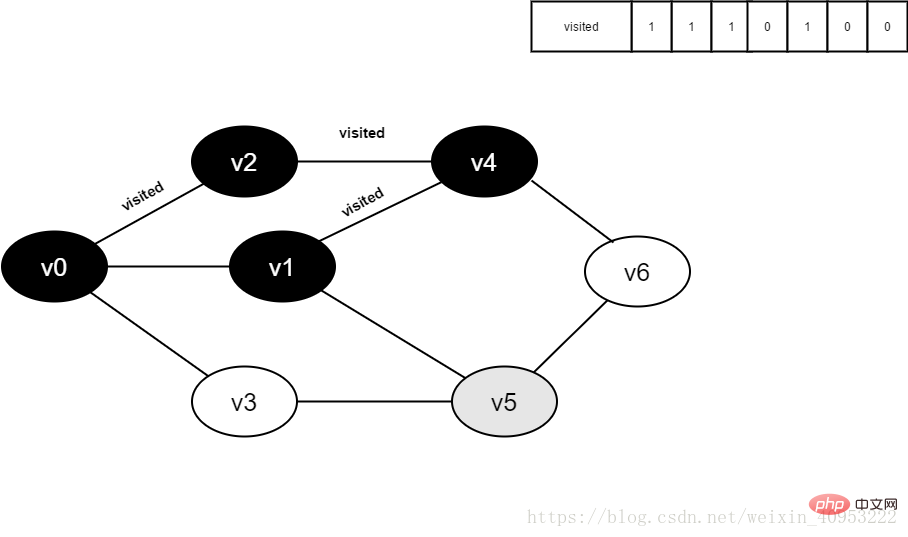
圖4-2-10
#11.將visited[5]置為1。
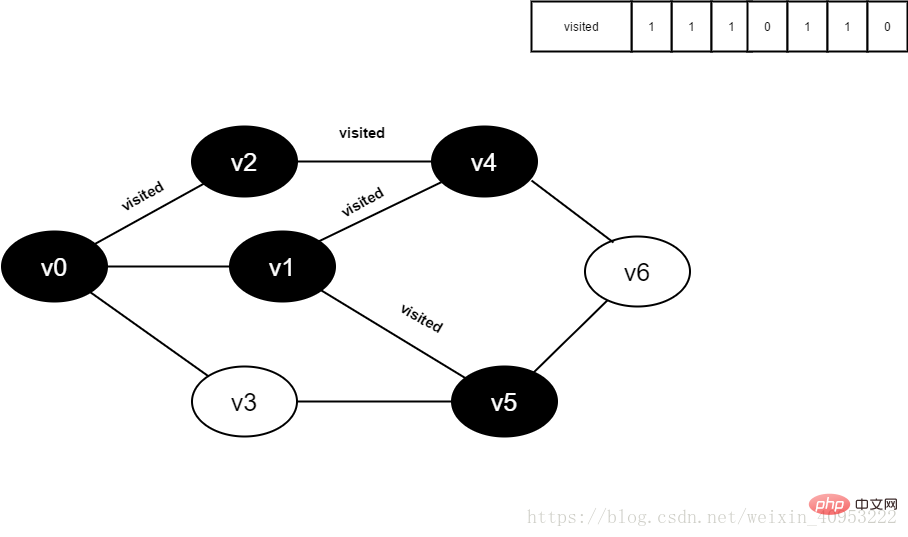
圖4-2-11
#12.訪問v5的鄰接點v1,判斷visited [1],其值為1,不訪問。
繼續訪問v5的鄰接點v3,判斷visited[3],其值為0,訪問v3。
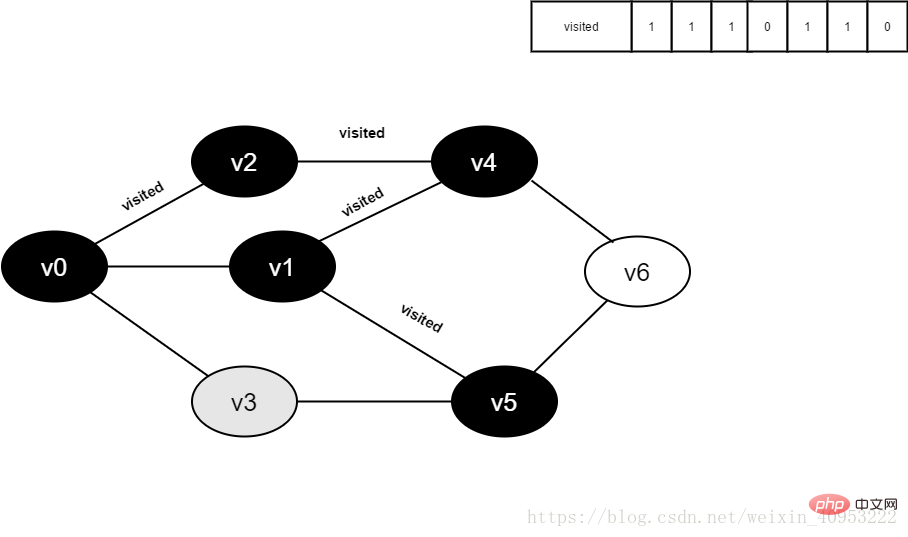
图4-2-12
13.将visited[1]置为1。
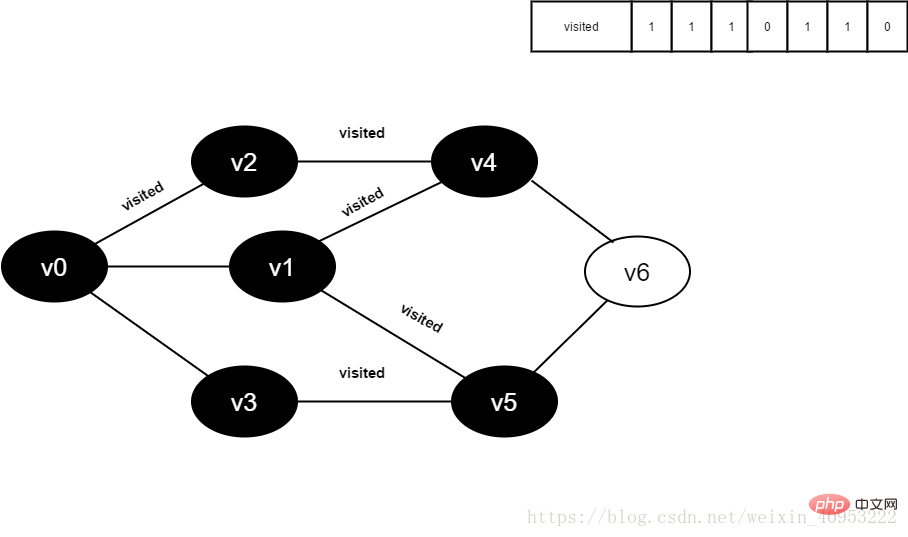
图4-2-13
14.访问v3的邻接点v0,判断visited[0],其值为1,不访问。
继续访问v3的邻接点v5,判断visited[5],其值为1,不访问。
v3所有邻接点均已被访问,回溯到其上一个顶点v5,遍历v5所有邻接点。
访问v5的邻接点v6,判断visited[6],其值为0,访问v6。
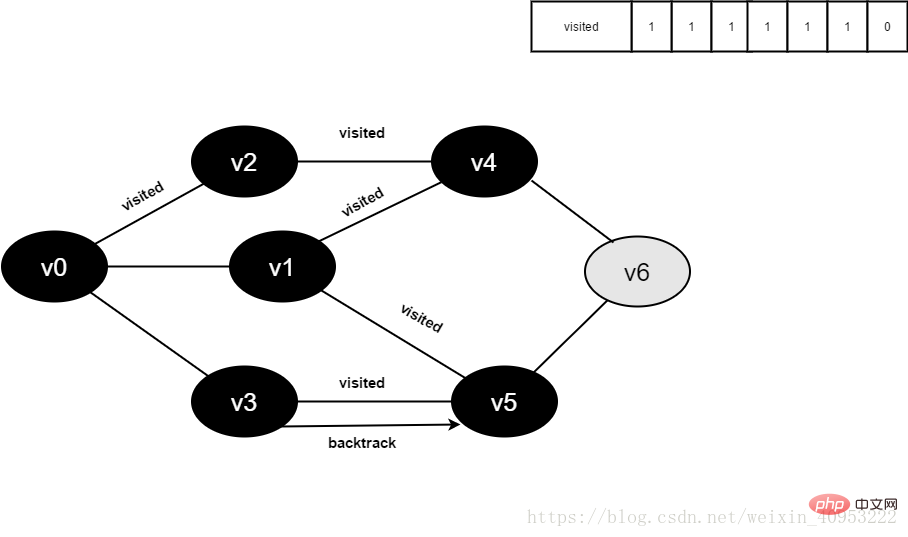
图4-2-14
15.将visited[6]置为1。
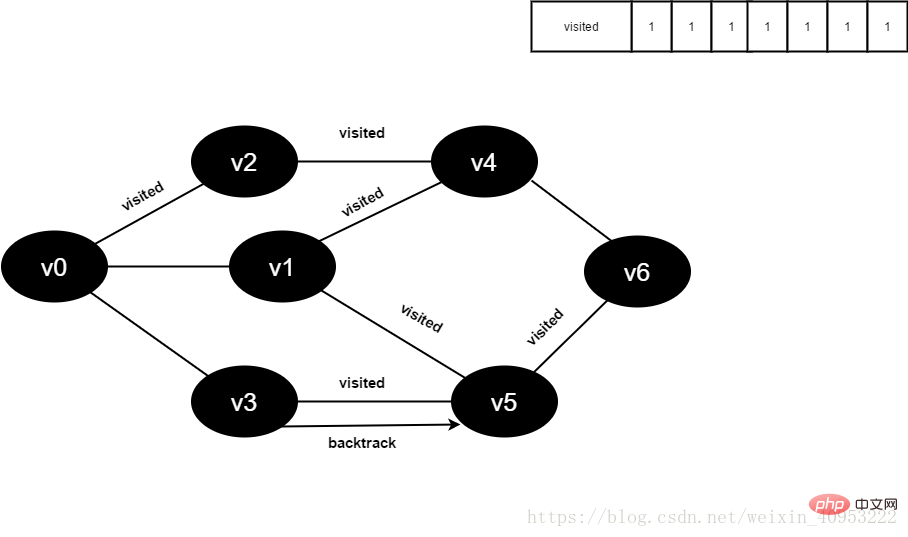
图4-2-15
16.访问v6的邻接点v4,判断visited[4],其值为1,不访问。
访问v6的邻接点v5,判断visited[5],其值为1,不访问。
v6所有邻接点均已被访问,回溯到其上一个顶点v5,遍历v5剩余邻接点。
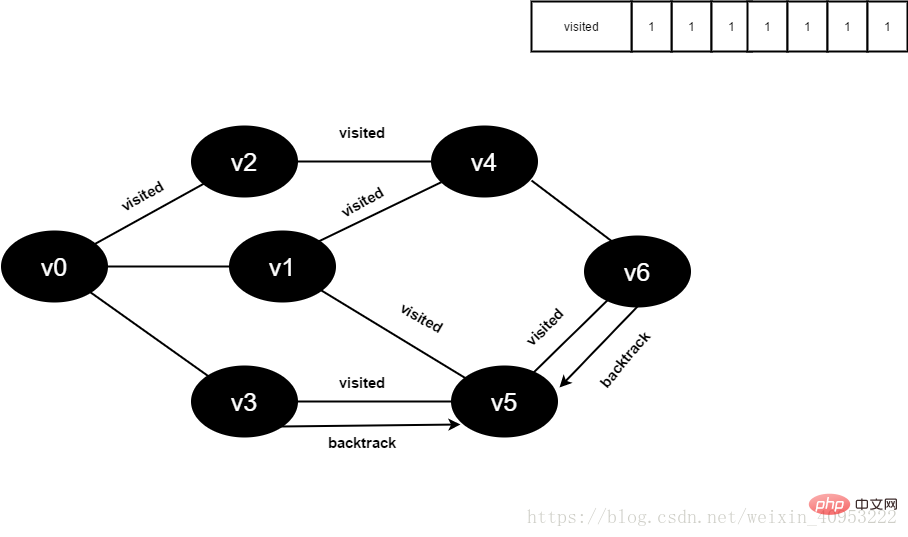
图4-2-16
17.v5所有邻接点均已被访问,回溯到其上一个顶点v1。
v1所有邻接点均已被访问,回溯到其上一个顶点v4,遍历v4剩余邻接点v6。
v4所有邻接点均已被访问,回溯到其上一个顶点v2。
v2所有邻接点均已被访问,回溯到其上一个顶点v1,遍历v1剩余邻接点v3。
v1所有邻接点均已被访问,搜索结束。
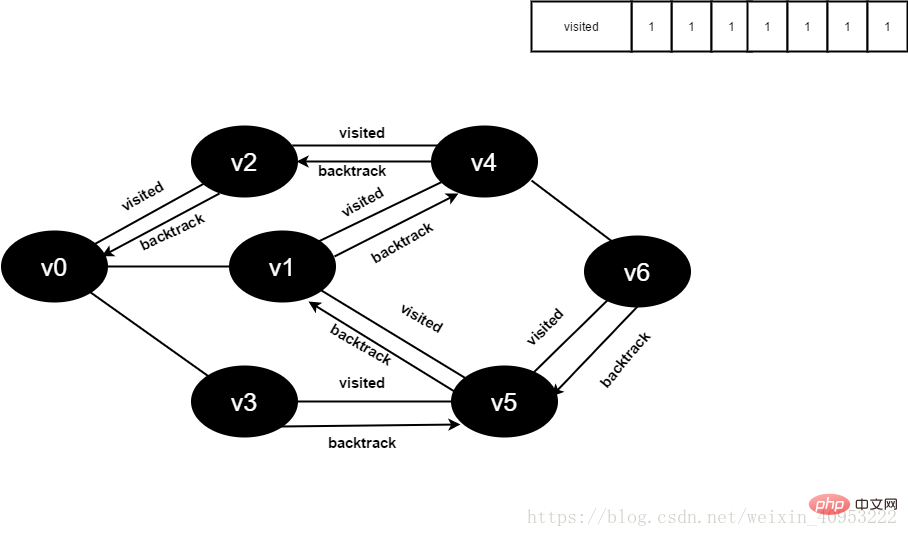
图4-2-17
4.3具体代码实现
4.3.1用邻接矩阵表示图的深度优先搜索
邻接矩阵的创建在上述已描述过,这里不再赘述
void DFS_AM(AMGraph &G, int v)
{
int w;
printf("%c ", G.vexs[v]);
visited[v] = 1;
for (w = 0; w < G.vexnum; w++)
if (G.arcs[v][w]&&!visited[w]) //递归调用
DFS_AM(G,w);
}4.3.2用邻接表表示图的深度优先搜素
邻接表的创建在上述已描述过,这里不再赘述。
void DFS_AL(ALGraph &G, int v)
{
int w;
printf("%c ", G.vertices[v].data);
visited[v] = 1;
ArcNode *p = new ArcNode;
p = G.vertices[v].firstarc;
while (p)
{
w = p->adjvex;
if (!visited[w]) DFS_AL(G, w);
p = p->nextarc;
}
}更多相关知识,请访问:PHP中文网!
以上是圖的廣度優先遍歷類似二元樹的什麼?的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 Java中的二元樹結構詳解
Jun 16, 2023 am 08:58 AM
Java中的二元樹結構詳解
Jun 16, 2023 am 08:58 AM
二元樹是計算機科學中常見的資料結構,也是Java程式設計中常用的資料結構。本文將詳細介紹Java中的二元樹結構。一、什麼是二元樹?在電腦科學中,二元樹是一種樹狀結構,每個節點最多有兩個子節點。其中,左側子節點比父節點小,右側子節點比父節點大。在Java程式設計中,常用二元樹表示排序,搜尋以及提高對資料的查詢效率。二、Java中的二元樹實作在Java中,二元樹
 在C語言中列印二元樹的左視圖
Sep 03, 2023 pm 01:25 PM
在C語言中列印二元樹的左視圖
Sep 03, 2023 pm 01:25 PM
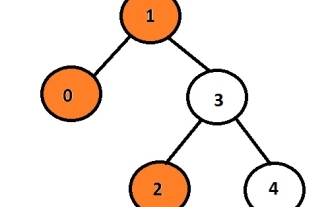
任務是列印給定二元樹的左節點。首先,使用者將插入數據,從而生成二元樹,然後列印所形成的樹的左側視圖。每個節點最多可以有2個子節點,因此這裡程式必須僅遍歷與節點關聯的左指針如果左指針不為空,則表示它將有一些與之關聯的資料或指針,否則它將是要列印並顯示為輸出的左子級。範例Input:10324Output:102這裡,橘色節點代表二元樹的左邊視圖。在給定的圖中,資料為1的節點是根節點,因此它將被列印,而不是轉到左子節點,它將列印0,然後它將轉到3並列印其左子節點,即2 。我們可以使用遞歸方法來儲存節點的級
 在C語言中,將二元樹的右側視圖列印出來
Sep 16, 2023 pm 11:13 PM
在C語言中,將二元樹的右側視圖列印出來
Sep 16, 2023 pm 11:13 PM
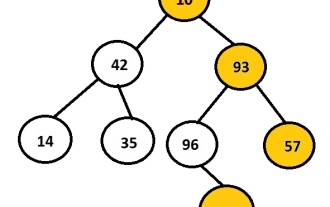
任務是列印給定二元樹的右節點。首先使用者將插入資料以建立二元樹,然後列印所形成的樹的右視圖。上圖展示了使用節點10、42、93、14、35、96、57和88建立的二元樹,其中選擇並顯示在樹的右側的節點。例如,10、93、57和88是二元樹的最右節點。範例Input:1042931435965788Output:10935788每個節點都有兩個指針,即左指針和右指針。根據這個問題,程式只需遍歷右節點。因此,不需要考慮節點的左子節點。右視圖儲存了所有那些是其所在層級的最後一個節點的節點。因此,我們可以
 如何使用Python實作二元樹的遍歷
Jun 09, 2023 pm 09:12 PM
如何使用Python實作二元樹的遍歷
Jun 09, 2023 pm 09:12 PM
作為一種常用的資料結構,二元樹經常被用來儲存資料、搜尋和排序。遍歷二元樹是非常常見的操作之一。 Python作為一種簡單易用的程式語言,有許多方法可以實作二元樹的遍歷。本文將介紹如何使用Python實現二元樹的前序、中序和後序遍歷。二元樹的基礎在學習二元樹的遍歷之前,我們需要先了解二元樹的基本概念。二元樹由節點組成,每個節點都有一個值和兩個子節點(左子節點和右子
 二元樹中等腰三角形的數量
Sep 05, 2023 am 09:41 AM
二元樹中等腰三角形的數量
Sep 05, 2023 am 09:41 AM
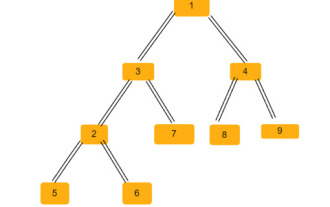
二元樹是一種資料結構,其中每個節點最多可以有兩個子節點。這些孩子分別稱為左孩子和右孩子。假設我們得到了一個父數組表示,您必須使用它來建立一棵二元樹。二元樹可能有幾個等腰三角形。我們必須找到該二元樹中可能的等腰三角形的總數。在本文中,我們將探討幾種在C++中解決這個問題的技術。理解問題給你一個父數組。您必須以二元樹的形式表示它,以便數組索引形成樹節點的值,而數組中的值給出該特定索引的父節點。請注意,-1始終是根父節點。下面給出的是一個數組及其二元樹表示。 Parentarray=[0,-1,3,1,
 PHP實作二元樹的方式與應用
Jun 18, 2023 pm 06:28 PM
PHP實作二元樹的方式與應用
Jun 18, 2023 pm 06:28 PM
在電腦科學中,二元樹是一種重要的資料結構。它由節點和指向它們的邊組成,每個節點最多連接兩個子節點。二叉樹的應用廣泛,例如搜尋演算法、編譯器、資料庫、記憶體管理等領域。許多程式語言都支援二元樹資料結構的實現,其中PHP是其中之一。本文將介紹PHP實作二元樹的方式以及其應用。二元樹的定義二元樹是一種資料結構,它由節點和指向它們的邊組成。每個節點最多連接兩個子節點,
 Java二元樹實作及具體應用案例詳解
Jun 15, 2023 pm 11:03 PM
Java二元樹實作及具體應用案例詳解
Jun 15, 2023 pm 11:03 PM
Java二元樹實作及具體應用案例詳解二元樹是一種經常在電腦科學中使用的資料結構,可以進行非常有效率的查找和排序操作。在本文中,我們將討論Java中如何實作二元樹及其一些具體應用案例。二元樹的定義二元樹是一種非常重要的資料結構,由根節點(樹頂節點)和若干個左子樹和右子樹組成。每個節點最多有兩個子節點,左邊的子節點稱為左子樹,右邊的子節點稱為右子樹。如果節點沒有
 PHP中的二元樹演算法及常見問題解答
Jun 09, 2023 am 09:33 AM
PHP中的二元樹演算法及常見問題解答
Jun 09, 2023 am 09:33 AM
隨著Web開發的不斷發展,PHP作為一種廣泛使用的伺服器腳本語言,其演算法和資料結構也越來越重要。在這些演算法和資料結構中,二元樹演算法是一個非常重要的概念。本文將介紹PHP中的二元樹演算法及其應用,以及常見問題的解答。什麼是二元樹?二元樹是一種樹狀結構,其中每個節點最多有兩個子節點,分別為左子節點和右子節點。如果節點沒有子節點,則稱為葉子節點。二元樹通常用於搜索