什麼叫遞迴

遞迴：

1、要呼叫自己本身；

2、要有一個趨於終止的條件。

（推薦教學：java課程）

下面以一個求階乘的範例簡單介紹一下：

public class recursion {
    public static int fac(int n) {
        if(n == 1){
            return 1; //终止条件
        }
        return n * fac(n-1); //调用自身
    }
    public static void main(String[] args) {
        System.out.println(fac(5));
    }
}
// 运行结果： 120

遞歸過程（第一個梯度)

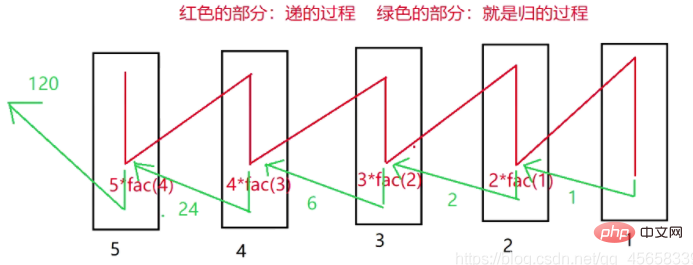
第二個維度： 方法的調用，需要在堆疊上開闢記憶體

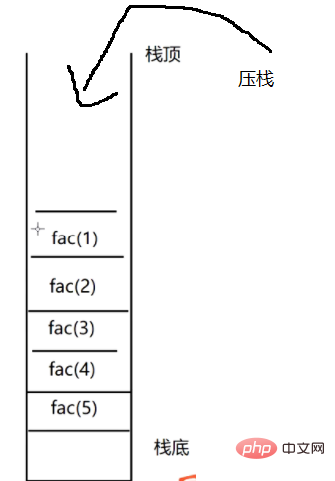
堆疊是先進後出的。

先呼叫 fac(5)，逐步呼叫 fac(4)… 直到終止條件。

壓端 的過程就是 遞 的過程。

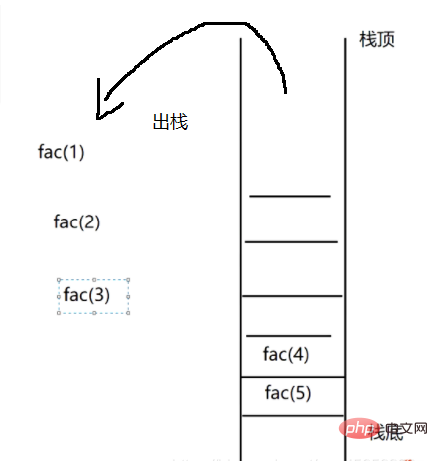
只要遇到終止條件 return，函數結束，逐步回傳 fac(n) 的值。

出棧 的 過程就是 歸 的過程。

相關推薦：java入門

以上是什麼叫遞迴的詳細內容。更多資訊請關注PHP中文網其他相關文章！