Python解決高等數學問題,媽媽再也不用擔心我的學習

#使用Python解決高等數學中極限、導數、偏導數、定積分、不定積分、雙重積分等問題
Sympy是一個Python的科學計算庫,它旨在成為功能齊全的計算機代數系統。 SymPy 包含從基本符號算術到微積分,代數,離散數學和量子物理學的功能。它可以在 LaTeX 中顯示結果。
Sympy官網
文章目錄
(免費學習推薦:python影片教學)

看到這圖,是不是感覺快喘不過氣了呢。 Python來幫你解決。輸入「x= symbols(“x」)」指令定義一個符號from sympy import *import sympy登入後複製
x = Symbol("x")y = Symbol("y")1. 實用技巧
1.1 符號函數
sympy提供了很多數學符號,總結如下sympy.I
sympy.E
sympy.oo
sympy.pi
sympy.root(8,3)
sympy.log(1024,2)
sympy.factorial(4)
sympy.sin(sympy.pi)sympy.tan(sympy.pi/4)sympy.cos(sympy.pi/2)
1.2 展開表達式expand
f = (1+x)**3expand(f)
x 3 + 3 x 2 + 3 x + 1 \displaystyle x^{3} + 3 x^{2} + 3 x + 1 x3+3x2+3x+1
1.3 泰勒展开公式series
ln(1+x).series(x,0,4)
x
−
x
2
2
+
x
3
3
+
O
(
x
4
)
\displaystyle x - \frac{x^{2}}{2} + \frac{x^{3}}{3} + O\left(x^{4}\正確的)
x− ##2 ################# # #2 ##3#x#3 ###牛#######)
x
−
x
3
6
+
x
5
120
−
x
7
5040
+
O
(
x
8
)
\displaystyle x - \frac{x^{3}}{6} + \frac{x^{5}}{120} - \frac{x^{7}}{5040} + O\left(x^{8}\正確的)
x− 6 ######### ### #3 ##120############ ###### #5 − 5040######### ########## #7 O( ##x#8 ##) #
1
−
x
2
2
+
x
4
24
−
x
6
720
+
x
8
40320
+
O
(
x
9
)
\displaystyle 1 - \frac{x^{2}}{2} + \frac{x^{4}}{24} - \frac{x^{6}}{720} + \frac{x^{8}}{40320} + O\left(x^{9}\正確的)
1− ##2 # ######### ## 2 24 ##x##4 #−720 ##x#6 ############4032#0 ############## #### #8O(##x#9 ##) #
1
−
x
+
x
2
−
x
3
+
x
4
+
O
(
x
5
)
\displaystyle 1 - x + x^{2} - x^{3} + x^{4} + O\left(x^{5}\正確的)
1− x#x #2−#x ##3 ############ ###### #4 #O (x ##5 ##) #
x
+
x
3
3
+
O
(
x
4
)
\displaystyle x + \frac{x^{3}}{3} + O\left(x^{4}\right)
x+3x3+O(x4)
1
+
x
+
x
2
+
x
3
+
O
(
x
4
)
\displaystyle 1 + x + x^{2} + x^{3} + O\left(x^{4}\right)
1+x+x2+x3+O(x4)
1
−
x
+
x
2
−
x
3
+
O
(
x
4
)
\displaystyle 1 - x + x^{2} - x^{3} + O\left(x^{4}\right)
1−x+x2−x3+O(x4) 1.4 符号展开
x
a
+
b
\displaystyle x^{a + b}
xa+b 2. 求极限limit
1
\displaystyle 1
1
(
x
+
1
)
1
x
\displaystyle \left(x + 1\right)^{\frac{1}{x}}
(x+1)x1 重要极限 dir可以表示极限的趋近方向
e
1
x
+
1
\displaystyle e^{\frac{1}{x}} + 1
ex1+1
1
\displaystyle 1
1
∞
\displaystyle \infty
∞ 3. 求导diff diff(函数,自变量,求导次数) 3.1 一元函数 求导问题
2
cos
(
2
x
)
\displaystyle 2 \cos{\left(2 x \right)}
2cos(2x)
1
x
\displaystyle \frac{1}{x}
x1 3.2 多元函数 求偏导问题
−
x
y
sin
(
x
y
)
+
cos
(
x
y
)
\displaystyle - x y \sin{\left(x y \right)} + \cos{\left(x y \right)}
−xysin(xy)+cos(xy) 4. 积分integrate 4.1 定积分
−
1.54366666666667
\displaystyle -1.54366666666667
−1.54366666666667
1
\displaystyle 1
1 4.2 不定积分
atan
(
x
)
\displaystyle \operatorname{atan}{\left(x \right)}
atan(x) 4.3 双重积分
11.6666666666667
\displaystyle 11.6666666666667
11.6666666666667 5. 求解方程组solve {x: -1, y: 4} 6. 计算求和式summation 计算求和式可以使用sympy.summation函数,其函数原型为sympy.summation(f, *symbols, **kwargs) 10100 到这里就结束了,如果对你有帮助,欢迎点赞关注评论,你的点赞对我很重要。在此也祝愿大家可以把数学学好 相关免费学习推荐:python教程(视频)sin(x).series(x,0,8)
cos(x).series(x,0,9)
(1/(1+x)).series(x,0,5)
tan(x).series(x,0,4)
(1/(1-x)).series(x,0,4)
(1/(1+x)).series(x,0,4)
a = Symbol("a")b = Symbol("b")#simplify( )普通的化简simplify((x**3 + x**2 - x - 1)/(x**2 + 2*x + 1))#trigsimp( )三角化简trigsimp(sin(x)/cos(x))#powsimp( )指数化简powsimp(x**a*x**b)limit(sin(x)/x,x,0)
f2=(1+x)**(1/x)
f2
f1=sin(x)/x
f2=(1+x)**(1/x)f3=(1+1/x)**x
lim1=limit(f1,x,0)lim2=limit(f2,x,0)lim3=limit(f3,x,oo)print(lim1,lim2,lim3)
1 E E
f4 = (1+exp(1/x))f4
lim4 = limit(f4,x,0,dir="-")lim4
lim5 = limit(f4,x,0,dir="+")lim5
diff(sin(2*x),x)
diff(ln(x),x)
diff(sin(x*y),x,y)
f = x**2 + 1integrate(f,(x,-1.1))
integrate(exp(x),(x,-oo,0))
f = 1/(1+x*x)integrate(f,x)
f = (4/3)*x + 2*y
integrate(f,(x,0,1),(y,-3,4))
#解方程组#定义变量f1=x+y-3f2=x-y+5solve([f1,f2],[x,y])
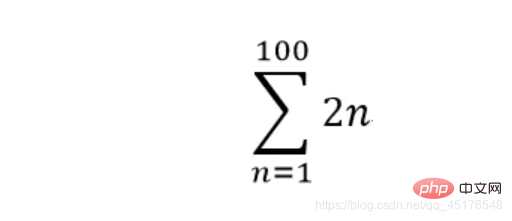
**sympy.summation(2 * n,(n,1,100))
以上是學習Python解決高等數學問題的詳細內容。更多資訊請關注PHP中文網其他相關文章!



