圖的儲存結構
圖的概念介紹得差不多了,大家可以消化消化再繼續學習後面的內容。如果沒有什麼問題的話,我們就繼續學習接下來的內容。當然,這還不是最麻煩的地方,因為今天我們只是介紹圖的儲存結構而已。
圖的順序儲存結構:鄰接矩陣
什麼是鄰接矩陣
首先還是來看看如何用順序結構來儲存圖。不管是堆疊、佇列、樹,我們都可以使用一個簡單的陣列就可以實作這些資料結構的順序儲存能力。但圖就不一樣了,從上篇文章中,我們學到過,一個結點的表示是
【推薦:PHP影片教學】
在圖的術語中,使用二維陣列來表示的圖的順序儲存結構就叫做鄰接矩陣。就像下面這個表格一樣。
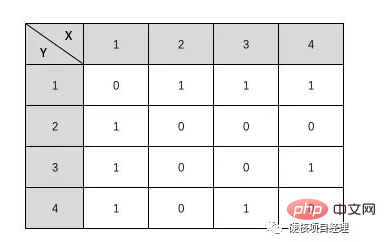
在這個表格中,我們有橫豎兩個座標,X1-4 和Y1-4 表示這個圖中一共有4 個結點,透過它們的對應關係就可以看做是一個結點與另一個結點之間是否有邊。比如說 X1 和 Y2 這一對座標
上面的這個鄰接矩陣對應的圖是什麼樣子的呢?大家可以自己嘗試手動畫一畫。畫不出來也不緊,因為我們才剛開始學嘛。其實它就是我們最開始展示的那張圖的鄰接矩陣。
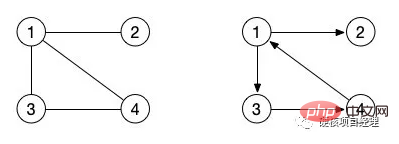
左邊的圖就是那個對應的我們上面的表格中的鄰接矩陣。那麼右邊那個有向圖的鄰接矩陣又是什麼樣子的呢?我們也寫寫試試。
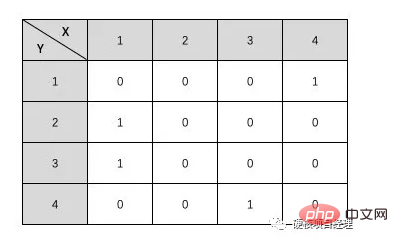
有意思吧?那如果是有權圖呢?其實很簡單的我們將圖中的1 直接換成對應邊的權值就可以了,不過有可能有的邊的權值就是0 ,所以在有權圖中,我們可以定義一個非常大的數,或定義一個非常小的負數當做無限數來表示這兩個結點沒有邊。
建構鄰接矩陣
接下來,我們就透過程式碼來建構這樣一個鄰接矩陣的儲存結構。我們還是用無向圖的例子來實現。因為無向圖是需要反向的結點也賦值的,所以它比有向圖多了一個步驟,而且它的基本上都是相似的。
// 邻接矩阵
$graphArr = [];
function CreateGraph($Nv, &$graphArr)
{
$graphArr = [];
for ($i = 1; $i <= $Nv; $i++) {
for ($j = 1; $j <= $Nv; $j++) {
$graphArr[$i][$j] = 0;
}
}
}
// 邻接矩阵
function BuildGraph(&$graphArr)
{
echo '请输入结点数:';
fscanf(STDIN, "%d", $Nv);
CreateGraph($Nv, $graphArr);
if ($graphArr) {
echo '请输入边数:';
fscanf(STDIN, "%d", $Ne);
if ($Ne > 0) {
for ($i = 1; $i <= $Ne; $i++) {
echo '请输入边,格式为 出 入 权:';
fscanf(STDIN, "%d %d %d", $v1, $v2, $weight);
$graphArr[$v1][$v2] = $weight;
// 如果是无向图,还需要插入逆向的边
$graphArr[$v2][$v1] = $weight;
}
}
}
}在這段程式碼中,首先我們透過 CreateGraph() 方法來初始化一個二維矩陣。也就是根據我們輸入的結點數量,實現一個 X * Y 的二維數組結構,並且定義它的所有值都是 0 ,也就是說,這個圖目前還沒有邊。
然後,在 BuildGraph() 方法調用完 CreateGraph() 之後,我們繼續輸入邊的資訊。先輸入邊的數量,我們有幾條邊,如果邊小於等於 0 的話就不要繼續創建了。其實還可以嚴謹一點根據 無向完全圖和有向完全圖 的定義來讓邊不能超過最大的限度。
接下來,我們就循環繼續輸入邊的信息,這裡我需要的輸入格式是邊的 出結點 、入結點 、權值。由於我們的範例是無向圖,所以我們除了要為
解釋程式碼可能還是比較抽象。直接運行一下試試吧。
BuildGraph($graphArr); // 请输入结点数:4 // 请输入边数:4 // 请输入边,格式为 出 入 权:1 2 1 // 请输入边,格式为 出 入 权:1 3 1 // 请输入边,格式为 出 入 权:1 4 1 // 请输入边,格式为 出 入 权:3 4 1 print_r($graphArr); // Array // ( // [1] => Array // ( // [1] => 0 // [2] => 1 // [3] => 1 // [4] => 1 // ) // [2] => Array // ( // [1] => 1 // [2] => 0 // [3] => 0 // [4] => 0 // ) // [3] => Array // ( // [1] => 1 // [2] => 0 // [3] => 0 // [4] => 1 // ) // [4] => Array // ( // [1] => 1 // [2] => 0 // [3] => 1 // [4] => 0 // ) // ) // x //y 0 1 1 1 // 1 0 0 0 // 1 0 0 1 // 1 0 1 0
在命令列環境中呼叫我們的 PHP 文件,然後根據提示的內容依序輸入相關的資訊。最後列印出來的陣列內容是不是就跟我們上面的表格中一模一樣了。簡簡單單的一段程式碼,我們就實作了圖的順序儲存。
可能有的同学会一时懵圈。因为我第一眼看到的时候也是完全懵了,不过仔细的对比画出来的图和上面的表格其实马上就能想明白了。这次我们真的是进入二维的世界了。是不是感觉图瞬间就把树甩到十万八千里之外了。完全二叉树的时候,我们的思想是二维的,但结构还是一维的,而到邻接矩阵的时候,不管是思想还是代码结构,全部都进化到了二维空间,高大上真不是吹的。
图的链式存储结构:邻接表
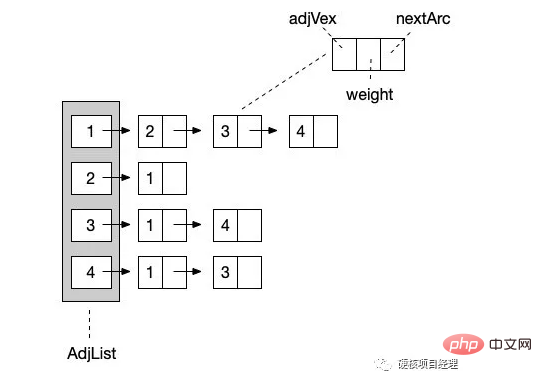
说完顺序存储结构,自然不能忽视另一种形式的存储结构,那就是图的链式存储结构。其实对于图来说,链式结构非常简单和清晰,因为我们只需要知道一个结点和那些结点有边就行了。那么我们就让这个结点形成一个单链表,一路往后链接就好了,就像下图这样。(同样以上图无向图为例)
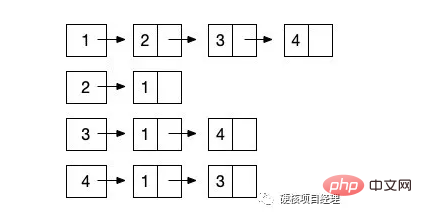
从 结点1 开始,它指向一个后继是 结点2 ,然后继续向后链接 结点3 和 结点4 。这样,与 结点1 相关的边就都描述完成了。由于我们展示的依然是无向图的邻接表表示,所以 结点2 的链表结点指向了 结点 1 。也就是完成了
对于代码实现来说,我们可以将头结点,也就是正式的 1-4 结点保存在一个顺序表中。然后让每个数组元素的值为第一个结点的内容。这样,我们就可以让链表结点只保存结点名称、权重和下一个结点对象的指向信息就可以了。
// 头结点
class AdjList
{
public $adjList = []; // 顶点列表
public $Nv = 0; // 结点数
public $Ne = 0; // 边数
}
// 边结点
class ArcNode
{
public $adjVex = 0; // 结点
public $nextArc = null; // 链接指向
public $weight = 0; // 权重
}
接下来,我们来看看如何使用邻接表这种结构来建立图。
function BuildLinkGraph()
{
fscanf(STDIN, "请输入 结点数 边数:%d %d", $Nv, $Ne);
if ($Nv > 1) {
// 初始化头结点
$adj = new AdjList();
$adj->Nv = $Nv; // 保存下来方便使用
$adj->Ne = $Ne; // 保存下来方便使用
// 头结点列表
for ($i = 1; $i <= $Nv; $i++) {
$adj->adjList[$i] = null; // 全部置为 NULL ,一个无边空图
}
if ($Ne > 0) {
//
for ($i = 1; $i <= $Ne; $i++) {
echo '请输入边,格式为 出 入 权:';
fscanf(STDIN, "%d %d %d", $v1, $v2, $weight);
// 建立一个结点
$p1 = new ArcNode;
$p1->adjVex = $v2; // 结点名称为 入结点
$p1->nextArc = $adj->adjList[$v1]; // 下一跳指向 出结点 的头结点
$p1->weight = $weight; // 设置权重
$adj->adjList[$v1] = $p1; // 让头结点的值等于当前新创建的这个结点
// 无向图需要下面的操作,也就是反向的链表也要建立
$p2 = new ArcNode;
// 注意下面两行与上面代码的区别
$p2->adjVex = $v1; // 这里是入结点
$p2->nextArc = $adj->adjList[$v2]; // 这里是出结点
$p2->weight = $weight;
$adj->adjList[$v2] = $p2;
}
return $adj;
}
}
return null;
}代码中的注释已经写得很清楚了。可以看出,在邻接表的操作中,无向图也是一样的比有向图多一步操作的,如果只是建立有向图的话,可以不需要 p2 结点的操作。特别需要注意的就是,在这段代码中,我们使用的是链表操作中的 头插法 。也就是最后一条数据会插入到 头结点 上,而最早的那个边会在链表的最后。大家看一下最后建立完成的数据结构的输出就明白了。
print_r(BuildLinkGraph()); // AdjList Object // ( // [adjList] => Array // ( // [1] => ArcNode Object // ( // [adjVex] => 4 // [nextArc] => ArcNode Object // ( // [adjVex] => 3 // [nextArc] => ArcNode Object // ( // [adjVex] => 2 // [nextArc] => // [weight] => 1 // ) // [weight] => 1 // ) // [weight] => 1 // ) // [2] => ArcNode Object // ( // [adjVex] => 1 // [nextArc] => // [weight] => 1 // ) // [3] => ArcNode Object // ( // [adjVex] => 4 // [nextArc] => ArcNode Object // ( // [adjVex] => 1 // [nextArc] => // [weight] => 1 // ) // [weight] => 1 // ) // [4] => ArcNode Object // ( // [adjVex] => 3 // [nextArc] => ArcNode Object // ( // [adjVex] => 1 // [nextArc] => // [weight] => 1 // ) // [weight] => 1 // ) // ) // [Nv] => 4 // [Ne] => 4 // )
使用邻接表来建立的图的链式存储结构是不是反而比邻接矩阵更加的清晰明了一些。就像树的链式和顺序结构一样,在图中它们的优缺点也是类似的。邻接矩阵占用的物理空间更多,因为它需要两层一样多元素的数组,就像上面的表格一样,需要占据 4 * 4 的物理格子。而邻接表我们可以直接数它的结点数,只需要 12 个格子就完成了。而且,更主要的是,链式的邻接表可以随时扩展边结点和边数,不需要重新地初始化,我们只需要简单地修改上面的测试代码就能够实现,而邻接矩阵如果要修改结点数的话,就得要重新初始化整个二维数组了。
总结
对于图来说,除了邻接矩阵和邻接表之外,还有其它的一些存储形式,不过都是链式的邻接表的一些优化和变形而已。大家有兴趣的可以自己去了解一下 十字链表 、邻接多重表 这两种存储结构。
好了,基础的存储结构已经铺垫完了,关于图的概念也都熟悉掌握了,接下来,我们就要准备去做最重要的操作了,那就是如何来对图进行遍历。
测试代码: https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/5.图/source/5.2图的存储结构.php
以上是PHP資料結構-圖的儲存結構的詳細內容。更多資訊請關注PHP中文網其他相關文章!




