引入：
其實K路歸併排序的用處還是很廣的，最簡單的，假設你要排序海量的數據，比如TB級別的數據（我們姑且說是TB級別的搜尋關鍵字），但是我們的記憶體只有GB級別，我們沒辦法一次把所有的資料全部載入然後排序，但是我們的確最終要結果，那麼怎麼辦呢？ K路歸併排序閃亮登場，其實這就是一個「分而治之」的思想，既然我們要排Q個數，但是我們不能一次頭全部排序完畢，這時候，我們把Q分為k組，每組n 個數,（k 分析： (1)如何合併k個已經排序了的陣列呢？ 因為我們以前討論過堆，顯然堆的排序效率是非常高的，所以我們自然也考慮到用堆來實現，因為要升序排列，所以我們創建一個最小堆。因為最終排序結果的數總是小的在前面大的在後面，所以我們考慮先把所有的n個數組的第一個元素（最小數）都放入最小堆中，所以最小堆的大小為k 。這樣我們調整堆結構，那麼它的第一個元素就是min( min(array1),min(array2)....min(arrayn))顯然就是所有數中的最小元素。 (2)因為在任意數組中都是按照升序排列的，所以我們一旦從堆中刪除了一個最小元素，就必須找一個元素來填這個坑。為此，我們需要找到刪除元素所在的陣列中的下一個元素然後將其填入堆疊。 （這個有點像是吧全國的最精英的士兵都拉去精英團打仗，那麼就是每個團的最強的都拉來，如果這個人不幸戰死，那麼從同團中找出僅次於它的繼續頂這個精英團，這樣永遠保持精英團的戰鬥力最高） 所以，如何去根據被刪除的堆元素找這個被刪除的堆元素所在的數組呢？這就需要在我們新建一個複合型別，它既包含目前的值，也包含這個目前值所在的陣列的id, (3)因為每個排序了的數組，隨著最小的元素的不斷流失，它還沒有參與排序的值是漸漸變少的，所以我們必須維護一個長度為k的數組，這個數組保留了每個數組中還沒參與排序的當前位置。並且一旦這個數組中剩餘的最小元素被添加到了堆，那麼這個當前位置必須後移。 (4)隨著每個陣列的目前位置後移，總歸最後會達到這個陣列的末端，這時候，這個陣列就不能再提供任何數了，（這個很正常，例如部隊中有一個尖刀連，它包含了最傑出的人，那麼最後選到精英團時，總從這個連隊選，然後這個連隊一定最後沒人了） ，所以我們就無法從當前刪除的數所在數組中找到下一個值了，這時候我們就必須選擇下一個有值的陣列id，並且挑選出其最小值，方法是arrayIdForDeletedData = (arrayIdForDeletedData 1) % k 。 (5)最後總有所有的數組位置都到了末端，也就是所有數組都不能提供未參與排序的值，所以這時候我們就要判斷當前的堆是否為空，如果不為空，那麼他們就包含了n*k中的最大的幾個數了，我們依次deleteMin()來吧最大的幾個數字按照最小順序輸出。如果目前的堆已經為空，那麼直接跳出循環。 所以最終時間複雜僅為 O(n*logk) #程式碼： #想清楚了上述幾個關鍵技術細節，這裡程式碼就很好寫了。 首先，我們定義一個值對象，它封裝了某個整數以及這個整數來自於哪個數組. 然後我們定義一個最小堆，它是解決問題的關鍵，需要注意的是，它所包含的元素應該是上述的值對象，當入堆，調整堆，基於的計算都是值對象的data欄位。 最後，我們來實作K路合併器，還是挺好實現的，不過涉及到一些下標運算必須特別小心。因為我們要通用，所以k和n都是傳進來的，實際上，我們如果事先規劃好k和n之後，完全不用在內部維護這些數，因為只要吧他們存入最小堆就行了。 實驗： 最後我們來示範下，假設我們有32個數，我們分成4路合併，每路8個數，而這8個數是已經排序的。 然後我們用K路合併演算法來對所有的32個數字進行排序： 最後運行結果為： package com.charles.algo.kwaymerge;
/**
*
* 这个对象表明是一个可以跟踪来自于哪个数组的数据对象
* @author charles.wang
*
*/
public class TrackableData {
//data表明具体的值
private int data;
//comeFromArray表明这个值来自于哪一个数组
private int comeFromArray;
public TrackableData(int data,int comeFromArray){
this.data = data;
this.comeFromArray=comeFromArray;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public int getComeFromArray() {
return comeFromArray;
}
public void setComeFromArray(int comeFromArray) {
this.comeFromArray = comeFromArray;
}
}package com.charles.algo.kwaymerge;
/**
* @author charles.wang
*
*/
public class MinHeap {
// 最小堆的存储是一个数组,并且为了计算，我们第一个位置不放内容
private TrackableData[] data;
// 堆的大小
private int heapSize;
// 当前元素的数量
private int currentSize;
public MinHeap(int maxSize) {
heapSize = maxSize;
// 创建一个比最大容纳数量多1的数组的作用是启用掉数组的头元素，为了方便运算，因为从1开始的运算更加好算
data = new TrackableData[heapSize + 1];
currentSize = 0;
}
/**
* 返回当前的堆是否为空
* @return
*/
public boolean isEmpty(){
if(currentSize==0)
return true;
return false;
}
/**
* 这里考察堆的插入，因为最小堆内部结构中数组前面元素总是按照最小堆已经构建好的，所以我们总从尾部插入 解决方法是： Step
* 1:先把当前的元素插入到数组的尾部 Step 2:递归的比较当前元素和父亲节点元素， Step
* 3:如果当前的元素小于父亲节点的元素，那么就把当前的元素上移，直到移不动为止
*
* @param value
* @return
*/
public MinHeap insert(TrackableData value) {
// 首先判断堆是否满了，如果满了就无法插入
if (currentSize == heapSize)
return this;
// 如果堆还没有满，那么说明堆中还有位置可以插入，我们先找到最后一个可以插入的位置
// currentPos表示当前要插入的位置的数组下标
int currentPos = currentSize + 1;
// 先插入到当前的位置，因为是从1开始的，所以数组下标运算也要+1
data[currentPos] = value;
// 然后比较当前元素和他的父亲元素
// 当前元素是data[currentPos] ，父亲元素是 data[(currentPos/2],一直遍历到根
TrackableData temp;
// 如果currentPos为1，表明是插入的堆中第一个元素，则不用比较
// 否则， 如果插了不止一个元素，则用插入位置的元素和其父元素比较
while (currentPos > 1) {
// 如果当前元素小于父亲元素，那么交换他们位置
if (data[currentPos].getData() < data[currentPos / 2].getData()) {
temp = data[currentPos / 2];
data[currentPos / 2] = data[currentPos];
data[currentPos] = temp;
// 更新当前位置
currentPos = currentPos / 2;
}
// 否则， 在假定已有的堆是最小堆的情况下，说明现在插入的位置是正确的，不用变换
else {
break;
}
}
// 插入完毕之后，吧当前的堆中元素的个数加1
currentSize++;
return this;
}
/**
* 这里考察堆的删除 因为是最小堆，所以肯定删除最小值就是删除堆的根元素，此外，还必须要调整剩余的堆使其仍然保持一个最小堆
* 因为有删除最小元素之后最小元素位置就有了个空位，所以解决方法是： Step 1:吧堆中最后一个元素复制给这个空位 Step
* 2:依次比较这个最后元素值，当前位置的左右子元素的值，从而下调到一个合适的位置 Step 3:从堆数组中移除最后那个元素
*/
public TrackableData deleteMin() {
// 如果最小堆已经为空，那么无法删除最小元素
if (currentSize == 0)
return null;
// 否则堆不为空，那么最小元素总是堆中的第一个元素
TrackableData minValue = data[1];
// 既然删除了最小元素，那么堆中currentSize的尺寸就要-1，为此，我们必须为数组中最后一个元素找到合适的新位置
// 堆中最后一个元素
TrackableData lastValue = data[currentSize];
// 先将堆中最后一个元素移动到最小堆的堆首
data[1] = lastValue;
// 把堆内部存储数组的最后一个元素清0
data[currentSize] = null;
// 并且当前的堆的尺寸要-1
currentSize--;
// 现在开始调整堆结构使其仍然为一个最小堆
int currentPos = 1; // 当前位置设置为根，从根开始比较左右
int leftPos = currentPos * 2;
TrackableData leftValue;
TrackableData rightValue;
TrackableData temp;
// 如果左位置和当前堆的总容量相同，说明只有2个元素了，一个是根元素，一个是根的左元素
if (leftPos == currentSize) {
// 这时候如果根左元素data[2]比根元素data[1]小，那么就交换二者位置
if (data[2].getData() < data[1].getData()) {
temp = data[2];
data[2] = data[1];
data[1] = temp;
}
}
else {
// 保持循环的条件是该节点的左位置小于当前堆中元素个数，那么该节点必定还有右子元素并且位置是左子元素位置+1
while (leftPos < currentSize) {
// 获取当前位置的左子节点的值
leftValue = data[leftPos];
// 获取当期那位置的右子节点的值
rightValue = data[leftPos + 1];
// 如果当前值既小于左子节点又小于右子节点，那么则说明当前值位置是正确的
if (data[currentPos].getData() < leftValue.getData()
&& data[currentPos].getData() < rightValue.getData()) {
break;
}
// 否则，比较左子节点和右子节点
// 如果左子节点小于右子节点（当然了，同时小于当前节点），那么左子节点和当前节点互换位置
else if (leftValue.getData() < rightValue.getData()) {
temp = data[currentPos];
data[currentPos] = leftValue;
data[leftPos] = temp;
// 同时更新当前位置是左子节点的位置,并且新的左子节点的位置为左子节点的左子节点
currentPos = leftPos;
leftPos = currentPos * 2;
}
// 如果右子节点小于左子节点(当然了，同时小于当前节点），那么右边子节点和当前节点互换位置
else {
temp = data[currentPos];
data[currentPos] = rightValue;
data[leftPos + 1] = temp;
// 同时更新当前位置是右子节点的位置,并且新的左子节点的位置为右子节点的左子节点
currentPos = leftPos + 1;
leftPos = currentPos * 2;
}
}
}
return minValue;
}
}package com.charles.algo.kwaymerge;
import java.util.ArrayList;
import java.util.List;
/**
*
* 这个类用于演示K路合并
*
* @author charles.wang
*
*/
public class KWayMerger {
private KWayMerger() {
}
/**
* k路合并，这里的指导思想如下：
*
* (1)首先构造一个最小堆，其中堆中的元素初始值为每个数组中的最小元素
* (2)每次从最小堆中打印并且删除最小元素，然后把这个最小元素所在的数组中的下一个元素插入到最小堆中 (3)每次（2）结束后调整堆来维持这个最小堆
*/
public static void mergeKWay(int k, int n, List<int[]> arrays) {
// 这里存储了所有每个数组的当前的下标,在没有开始插入之前，每个数组的当前下标都设为0
int[] indexInArrays = new int[k];
for (int i = 0; i < k; i++) {
indexInArrays[i] = 0;
}
// 首先构造一个最小堆,其大小为k
MinHeap minHeap = new MinHeap(k);
// 第一步，依次吧每个数组中的第一个元素都插入到最小堆
// 然后把所有数组的下标都指向1
for (int i = 0; i < k; i++) {
// 这里每个都构造TrackableData对象：
// 其中：arrays.get(i)[0]表示它值为第i个数组的下标为0的元素（也就是第i个数组的第一个元素）
// i表示这个对象来自于第i个数组
minHeap.insert(new TrackableData(arrays.get(i)[0], i));
indexInArrays[i] = 1;
}
// 第二步，对最小堆进行反复的插入删除动作
TrackableData currentDeletedData;
TrackableData currentInsertedData;
int arrayIdForDeletedData;
int nextValueIndexInArray;
// 循环的条件是k个数组中至少有一个还有值没有被插入到minHeap中
while (true) {
// 这个变量维护了有多少个数组当前下标已经越界，也就是数组所有元素已经被完全处理过
int noOfArraysThatCompletelyHandled = 0;
// 就是去查询维护所有数组当前下标的数组，如果都越界了，那么就说明都比较过了
for (int i = 0; i < k; i++) {
if (indexInArrays[i] == n)
noOfArraysThatCompletelyHandled++;
}
// 如果所有的数组中的所有的值都比较过了，那么查看堆中内容是否为空。
if (noOfArraysThatCompletelyHandled == k) {
while (!minHeap.isEmpty()) {
currentDeletedData = minHeap.deleteMin();
// 打印出当前的数
System.out.print(currentDeletedData.getData() + " ");
}
break;
}
currentDeletedData = minHeap.deleteMin();
// 打印出当前的数
System.out.print(currentDeletedData.getData() + " ");
// 获取当前的被删的数来自于第几个数组
arrayIdForDeletedData = currentDeletedData.getComeFromArray();
// 获取那个数组的当前下标
nextValueIndexInArray = indexInArrays[arrayIdForDeletedData];
// 如果当前下标没有越界，说明当前数组中还有元素，则找到该数组中的下个元素
if (nextValueIndexInArray < n) {
// 构造新的TrackableData，并且插入到最小堆
currentInsertedData = new TrackableData(
arrays.get(arrayIdForDeletedData)[nextValueIndexInArray],
arrayIdForDeletedData);
minHeap.insert(currentInsertedData);
// 同时更新维护数组当前下标的数组，让对应数组的当前下标+1
indexInArrays[arrayIdForDeletedData]++;
}
// 如果当前下标已经越界，说明这个数组已经没有任何元素了，则找下一个有值的数组的最小元素
else {
while (true) {
arrayIdForDeletedData = (arrayIdForDeletedData + 1) % k;
// 获取那个数组的当前下标
nextValueIndexInArray = indexInArrays[arrayIdForDeletedData];
if (nextValueIndexInArray == n)
continue;
else {
// 构造新的TrackableData，并且插入到最小堆
currentInsertedData = new TrackableData(
arrays.get(arrayIdForDeletedData)[nextValueIndexInArray],
arrayIdForDeletedData);
minHeap.insert(currentInsertedData);
// 同时更新维护数组当前下标的数组，让对应数组的当前下标+1
indexInArrays[arrayIdForDeletedData]++;
break;
}
}
}
}
}
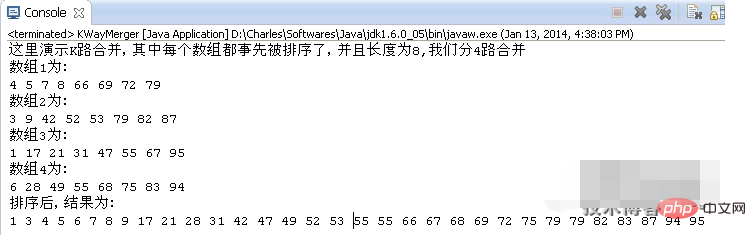
}public static void main(String[] args) {
// 我们来演示K路合并，假设我们有4组已经排序了的数组，每组有8个数，则n=8,k=4
int[] array1 = { 4, 5, 7, 8, 66, 69, 72, 79 };
int[] array2 = { 3, 9, 42, 52, 53, 79, 82, 87 };
int[] array3 = { 1, 17, 21, 31, 47, 55, 67, 95 };
int[] array4 = { 6, 28, 49, 55, 68, 75, 83, 94 };
System.out.println("这里演示K路合并，其中每个数组都事先被排序了，并且长度为8,我们分4路合并");
System.out.println("数组1为：");
for(int i=0;i<array1.length;i++)
System.out.print(array1[i]+" ");
System.out.println();
System.out.println("数组2为：");
for(int i=0;i<array2.length;i++)
System.out.print(array2[i]+" ");
System.out.println();
System.out.println("数组3为：");
for(int i=0;i<array3.length;i++)
System.out.print(array3[i]+" ");
System.out.println();
System.out.println("数组4为：");
for(int i=0;i<array4.length;i++)
System.out.print(array4[i]+" ");
System.out.println();
List<int[]> arrayLists = new ArrayList<int[]>(4);
arrayLists.add(0, array1);
arrayLists.add(1, array2);
arrayLists.add(2, array3);
arrayLists.add(3, array4);
KWayMerger kWayMerger = new KWayMerger(4, 8, arrayLists);
System.out.println("排序后，结果为：");
kWayMerger.mergeKWay();
System.out.println();
}
以上是詳解K路歸併排序（實戰）的詳細內容。更多資訊請關注PHP中文網其他相關文章！
