在上篇文章中，我們學習了二元樹的基本鍊式結構以及建樹和遍歷相關的操作。今天我們學習的則是一些二元樹相關的概念以及二元樹的一種變形形式。
什麼叫完全二元樹呢？在說到完全二元樹之前，我們先說另一個名詞：「滿二叉樹」。像我們之前文章中示範過的那個二元樹，就是一顆「滿二叉樹」。在這顆樹中，所有的結點都有兩個孩子結點，沒有哪個結點是只有一個孩子結點的，並且所有最底層的葉子結點都在同一層，這種樹就稱為“滿二元樹”，也稱為“完美二元樹”。
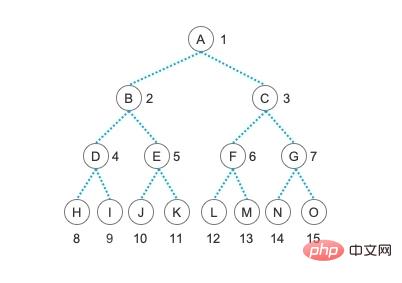
是不是非常漂亮的樹？沒錯，這種二元樹非常完美，它沒有多餘的結點，也沒有缺少的結點，非常的漂亮。但是，在現實中，完美的東西是很稀少的，人生總會有一點缺失。我們盡量不要讓自己有太多的缺憾，但也總不能過沒有一絲缺憾的人生。所以，我們允許葉結點出現在最下層和次下層，而且最下層的葉結點集中在樹的左部，也就是葉結點只能有左子樹，那麼，這樣的一顆略帶缺失的樹就叫做「完全二元樹」。不要擔心它不完美，因為這樣略帶缺失的人生才是完整的嘛，所以「完全二元樹」是一種理想的樹狀結構。
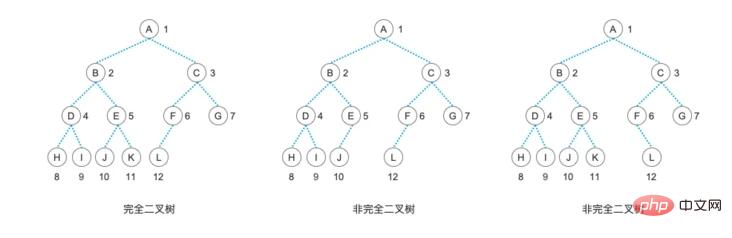
從定義中，我們可以看出，一顆“滿二叉樹”，必定是一顆“完全二叉樹”，而一顆葉子結點都在一層的並且所有結點都有左右孩子結點的“完全二叉樹”也就是一顆”滿二叉樹“。
為什麼要講」滿二元樹「和」完全二元樹「呢？當然是為了我們接下來的內容做鋪墊。因為」滿二叉樹「是最符合二元樹性質的一顆樹。還記得樹系列的第一篇文章中介紹過的二元樹的那五個性質嗎？當時我們就是以那顆”滿二叉樹「為例進行講解的。而其中的 性質5 ，就是我們學習使用順序結構來儲存二元樹的基礎。
透過」滿叉樹「的概念，以及二元樹的 性質5 我們就可以實現使用一個陣列來儲存順序結構的實作。
$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O'];
相信大家不陌生吧，在上篇文章中，我們就是透過這個陣列來建立鏈樹的，而這個陣列其實就是一個線性儲存的二元樹。我們透過對比二元樹的 性質5 來看一下。
A 結點的下標是 1 ，它是我們的樹根。它的子結點是 B 和 C ，對應的下標分別是 2 和 3 ，也就是 1 2 和 1 2 1 。
同理，我們再選取一個結點 F 。它的下標是 6 ，所以它的左孩子結點的下標是 6 2 = 12 ，對應的是 L ；它的右孩子結點是 6 2 1 = 13 ，對應的是 M 。
反過來看，一個結點的父結點就是 i / 2 。我們看下K 結點的下標是11 ，它的父結點就是11 / 2 ，捨去小數點是下標5 的位置，也就是結點E ；結點J 的下標是10 ，它的父結點是10 / 2 ，也是下標為5 的E 結點。
這下想以大家就明白了用數組是如何表示一顆二元樹結構了吧。而數組這種結構更加的一維，更能體現出對於樹的操作就是二維化一維的一種表示，也就是非線性轉線性，這樣才能讓我們方便地操作這些數據。
針對順序儲存結構，也就是陣列元素的遍歷，也是可以使用先序、中序、後序以及層序的形式。不過這些遍歷方法都需要根據二元樹的 性質5 來進行遍歷。但更重要的是，只要給我一個下標，我們透過二元樹的性質，就可能很容易知道它的下級結點和上級結點的位置，能夠快速地獲得這些結點的資訊。這一大特點是鍊式結構的二元樹所沒有的。
如果我們要儲存的不是一顆」滿二叉樹「呢？甚至它都不是一顆完全二元樹的情況下，只需要將對應的結點設為空值就行了。例如：
$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'I', '', '', '', '', 'H', '', 'J', '', ''];
這顆樹的結構所對應的二元樹圖形就是這樣的：
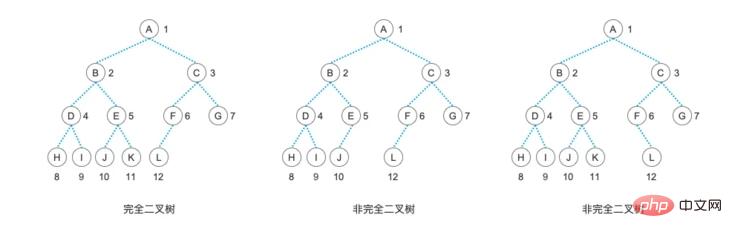
然後在建鏈樹的方法中，我們只需要再增加一個判斷就可以了。我們就可以透過這樣一個順序儲存的二元樹快速地產生一顆鍊式儲存的二元樹，方便我們之後的操作。
// 建立二叉树
function CreateBiTree($arr, $i)
{
if (!isset($arr[$i]) || !$arr[$i]) { // 这里增加了个判断，如果数组元素为空
return null;
}
$t = new TBTNode();
$t->data = $arr[$i];
$t->lChild = CreateBiTree($arr, $i * 2);
$t->rChild = CreateBiTree($arr, $i * 2 + 1);
return $t;
}一環套一環，接下來我們再來講講」線索二元樹「。這又是什麼東西呢？
从上面的学习中，我们知道了”满二叉树“和”完全二叉树“。但是这种结构都是非常理想的树结构，不过真实的情况可能大部分都是”理想很丰满，现实很骨感“。很多树并不能形成那样的完全二叉树的形式，更别提”满二叉树“了。而树的遍历又经常会使用栈或者队列来实现，这两种遍历方式基本都是线性的，也就是最好情况下也是 O(n) 的时间复杂度。那么，有没有什么更快一点的方式来提高遍历的效率呢？
我们这样来尝试一下：
如果树的叶子结点的左孩子结点为空，就让它指向前驱（上级）结点
如果树的叶子结点的右孩子结点为空，就让它指向后继结点
这样有什么好处呢？我们可以避免掉大范围的递归操作，从而加快树的遍历速度。在整个算法中，它并没有什么优势，因为我们需要将一颗树进行线索化，也就是去改变它的叶子结点的左右孩子的指向，这也是一次遍历。但是，如果你的操作是经常需要遍历，而且是来回的多次遍历，那么它的整体性能是要强于普通二叉树的遍历的。因为在一次线索化之后，它的遍历就是在快速的查找叶子结点的基础上进行普通的线性遍历操作，而不是递归操作。
对于线索二叉树来说，我们需要改变树的结点存储数据结构。
// 线索二叉树结点
class TBTNode
{
public $data;
public $lTag = 0;
public $rTag = 0;
public $lChild;
public $rChild;
}我们增加了两个标志位，当 $lTag 或 $rTag 为 1 时，$lChild 或 $rChild 分别指向前驱或后继结点。这样在最后的遍历时，我们就可以快速地通过这个 tag 标志位分辨出结点的指向状态。
然后我们先简单地建立一颗树。使用上一节中的那个示例。
// 建立二叉树
function CreateBiTree($arr, $i)
{
if (!isset($arr[$i]) || !$arr[$i]) { // 这里增加了个判断，如果数组元素为空
return null;
}
$t = new TBTNode();
$t->data = $arr[$i];
$t->lChild = CreateBiTree($arr, $i * 2);
$t->rChild = CreateBiTree($arr, $i * 2 + 1);
return $t;
}
$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'I', '', '', '', '', 'H', '', 'J', '', ''];
$tree = CreateBiTree($treeList, 1);接下来就是最重要的线索化过程，我们可以建立前序、中序、后序的线索二叉树。对应的，在最后的线索二叉树遍历时获得的结果也将是这三种遍历方式所对应的结果。在这里，我们学习最普遍的也是最经典的”中序线索二叉树“。所以，我们以中序遍历的形式将这颗树线索化。
// 线索化
function InThread(?TBTNode $p, ?TBTNode &$pre)
{
if ($p) {
// 递归，左子树线索化
InThread($p->lChild, $pre);
if (!$p->lChild) {
// 建立当前结点的前驱线索
$p->lChild = $pre;
$p->lTag = 1;
}
if ($pre && !$pre->rChild) {
// 建立当前结点的后继线索
$pre->rChild = $p;
$pre->rTag = 1;
}
$pre = $p; // $pre 指向当前的 $p ，作为 $p 将要指向的下一个结点的前驱结点指示指针
$p = $p->rChild; // $p 指向一个新结点，此时 $pre 和 $p 分别指向的结点形成了一个前驱后继对，为下一次线索化做准备
// 递归，右子树线索化
InThread($p, $pre);
}
}
// 创建线索二叉树
function createInThread(TBTNode $root)
{
$pre = null; // 前驱结点指针
if($root){
InThread($root, $pre);
$pre->rChild = null; // 非空二叉树，线索化
$pre->rTag = 1; // 后处理中序最后一个结点
}
}
createInThread($tree);
var_dump($tree);
// object(TBTNode)#1 (5) {
// ["data"]=>
// string(1) "A"
// ["lTag"]=>
// int(0)
// ["rTag"]=>
// int(0)
// ["lChild"]=>
// object(TBTNode)#2 (5) {
// ["data"]=>
// string(1) "B"
// ["lTag"]=>
// int(0)
// ["rTag"]=>
// int(0)
// ["lChild"]=>
// object(TBTNode)#3 (5) {
// ["data"]=>
// string(1) "D"
// ["lTag"]=>
// int(1)
// ["rTag"]=>
// int(1)
// ["lChild"]=>
// NULL
// ["rChild"]=>
// *RECURSION*
// }
// ……关于算法的具体步骤在注释中已经写得很详细了。一句话总结就是在中序遍历的过程中，根据结点的信息来确定它的左右孩子的形式，如果有左右孩子就继续，如果没有任一一个孩子的话，就将左右结点指向前驱或者后继。建立之后的线索二叉树就如图所示：
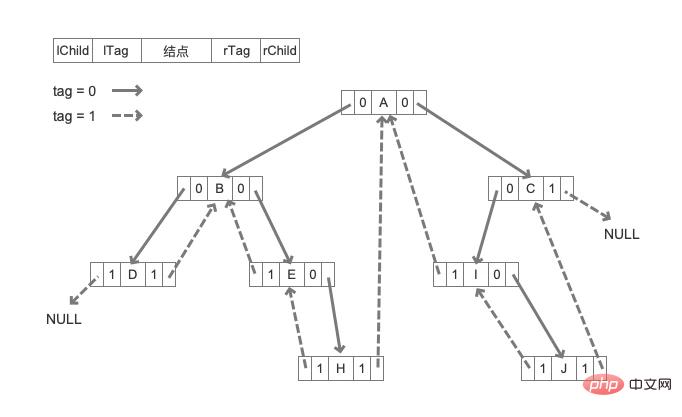
最后就是遍历了。我们需要的是能够快速地获得最左叶子结点的信息，然后就是下一跳的信息，这时，线索的威力就发挥出来了。
// 以 $p 为根的中序线索二叉树中，中序序列下的第一个结点，也就是最左边那个结点
function First(?TBTNode $p){
while($p->lTag == 0){
$p = $p->lChild; // 最左下结点（不一定是叶子结点）
}
return $p;
}
// 在中序二叉树中，结点 $p 在中序下的后继结点
function NextNode(?TBTNode $p){
if($p->rTag == 0){
return First($p->rChild);
}else{
return $p->rChild; // 如果 rTag == 1 ，直接返回后继线索
}
}
// 在中序线索二叉树上进行中序遍历
function Inorder(TBTNode $root){
// 第一个结点 结点不为空 下一个结点
for($p = First($root);$p;$p=NextNode($p)){
echo $p->data, ',';
}
}
Inorder($tree); // D,B,E,H,A,I,J,C,当遇到 $lTag 不为 0 的结点时，这个结点就是最左的那个结点了，如果这个不为空的话，【输出】它。接着我们获得下一跳的结点，也就是判断这个结点的右孩子 $rTag 标志，如果是为 0 的，也就是它还有右孩子，【输出】后向下查找，直到找到一个 $rTag 也为 1 的结点，直接返回这个结点的后继，也就是中序遍历的中间那个结点，【输出】它。
最后输出的顺序是不是和我们中序遍历的结果一样呢？注意看代码，在遍历中序线索二叉树的时候，我们没有用一个递归吧，全部是使用的 while() 和 for() 就完成了对这个线索二叉树的遍历。
坚持到现在不容易，不能再小看数据结构了吧？现在还只是树，我们的图都还没开始呢！当然，也不要害怕，一步一步的学，慢慢掌握，不要幻想一口气吃成个胖子。写完这篇文章我也不可能马上就手写出一个中序的线索二叉树来的。大家还是以理解原理为主，如果说真能手写的话，那也是为了面试而去背的或者是为了考研而准备的。这样的小同学在面试中我反而要更多问一些其它的问题，毕竟临时抱佛脚的准备远不如深入理解带来的感悟更能打动人！
测试代码：
https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/4.树/source/4.3完全二叉树、线索二叉树及树的顺序存储结构.php
推荐学习：php视频教程
以上是什麼是完全二元樹和線索二元樹？它們的順序儲存結構又是什麼樣的呢？的詳細內容。更多資訊請關注PHP中文網其他相關文章！
