隨著學習的深入,我們的知識也不斷擴展的豐富。樹狀結構有沒有讓大家蒙圈呢?相信我,學完圖以後你會覺得二元樹簡直是簡單到沒辦法說了。其實我們說說所的樹,也是圖的一種特殊形式。
還記得我們學習樹的第一篇文章時看到的那張關於樹的圖片嗎?
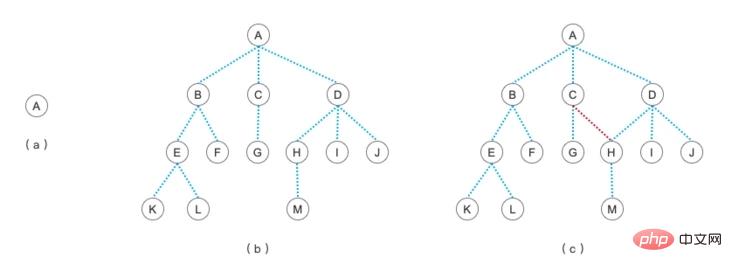
在當時,我們就說過,圖c 不是一顆樹,而是一個圖。為什麼呢?從樹的定義我們可以看出,樹只能有一個根結點,平級之間不能有聯繫,可以有多個子結點。而圖就不用遵守這些規則,圖的特點就是結點之間都可以互相有連結。例如下圖這樣的都是圖。
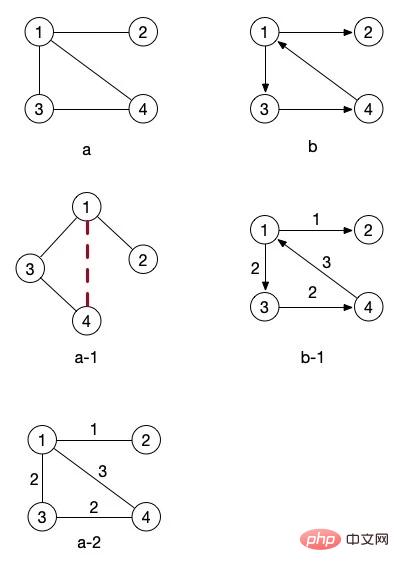
在上面所畫的圖中,圖b 是的箭頭的,而圖a 的連接線是沒有箭頭的,像這樣有明確的方向的指向的圖就叫做有向圖。而沒有箭頭的,也就是沒有方向指向的圖就叫作 無向圖 。
我們先將目光移到 圖a-1 ,其實它就是把 圖a 旋轉了一下。大家看得出來了嗎?如果忽略掉結點 4 和 1 之間的連線,那麼它就是一顆樹。是不是跟我們上面關於樹的圖中的 圖c 的概念一致了。
關於圖的比較正式的官方定義是:
圖(Graph)G 由兩個集合V 和E 組成,記為G=(V, E) ,其中V 是頂點的有窮非空集合,E 是V 中頂點的有窮集合,這些頂點偶對稱為邊。
在 有向圖 中,連接兩點的那個線段,從開始的結點到指向的那個結點可以記為
是不是覺得在看上面的圖片的時候還比較清晰,一看這個定義就一臉懵逼了?像這種定義,如果你是需要考試的同學,那就還是要背下來的。如果只是像我一起想以學習應用或了解為主的話,就不用去死記硬背了。 V 就是結點,E 就是這些這些結點之間的關係,兩個頂點之間的關係,也就是圖上的那些連接結點的線段就是邊。
OK,這三個最最基礎的概念搞明白了,我們就繼續學習其它的和圖有關的那一大車術語!
首先,我們用 n 來表示圖中頂點的數目,用 e 來表示邊的數目,記住這兩個代號。
(1)子圖:假設有兩個圖G=(V, E) 和G'=(V', E') 如果V' 包含於V 且E'包含於E ,則稱G' 為G 的子圖
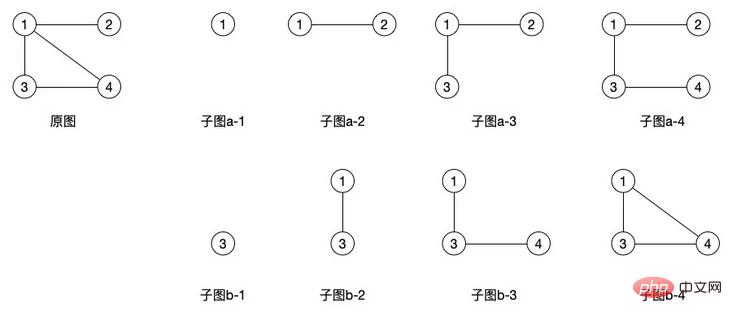
上圖中右邊的那些子圖都是屬於原圖的子圖,可以看出子圖可以產生非常多的形態,有向圖也是相同的概念,不過相對於無向圖來說,有向圖能夠產生的子圖更少一些,因為它的邊是有方向的。
(2) 無向完全圖和有向完全圖:對於無向圖,若具有 n(n-1)/2 條邊,就是無向完全圖。對於有向圖,若具有 n(n-1) 條孤,就稱為有向完全圖。 (參考完全二元樹)
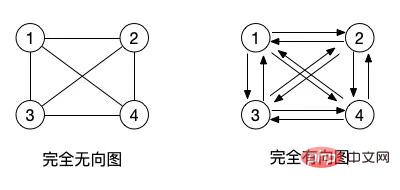
其實完全圖的概念就是圖中所有相鄰的結點都有邊能夠連結在一起。
對於有向圖來說,雖說邊是有方向的,當然我們也可以定義一個來回的方向,例如 和 ,在有向圖中我們就要畫上兩個相反方向的箭頭表示可以從1到2也可以從2到1。而 無向圖 中則是用一邊來代替這兩邊的概念了,本身的那一條沒有箭頭方向的邊就是雙向的。
(3) 稀疏圖與稠密圖:很少條邊或孤(如e
#(4) 權與網:在實際應用中,每條邊或孤可以標上具有某種意義的值,就像地圖上的距離一樣,這些數值就稱為權。帶權的圖就可以稱為網
最上方的圖片上 圖a-2 和 圖b-1 的邊上的數字代表的就是權重。這兩張圖就可以稱為網圖。權重的概念我們後面在講相關的演算法時會學習到,從這兩張圖中,我們其實就可以很明顯的看出,如果要從結點1 走到結點4 的話,並不是直接走 這條邊,而是走 、 這條路線更快。
(5) 鄰接點:兩個有邊的結點就是鄰接點
(6) 度、入度和出度:頂點v 的度就是指和v 相關聯的邊的數目。對於有向圖來說,箭頭指向其它結點的就是出度,指向自己的就是入度
#還是繼續來看 圖b 。結點1 有兩個出度,一個入度。這個貌似不用解釋太多了吧。
(7) 路徑和路徑長度:從某一個頂點到另一個頂點所經過的所有頂點就是路徑。如果是有向圖,那麼它的路徑就是按照箭頭的方向。路徑長度就是一條路徑上經過的邊或孤的數量
(8) 迴路或環:第一個頂點和最後一個頂點相同的路徑稱為迴路或環
(9) 連通、連通圖與連通分量:如果某兩個結點之間是有路徑的,就稱這兩個結點是連通的。如果整個圖中所有的結點都可以是互連通的,則這個圖就是連通圖。連通分量就是無向圖非連通圖中的極大連通子圖。
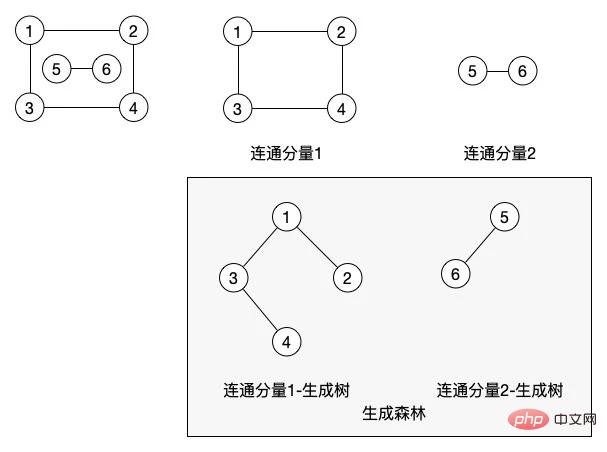
包含後面的三個概念也在這張圖中一併給出了。在 無向圖 中,連通分量就等於極大連通子圖,在這個圖中,我們有兩個連通分量。
(10) 極大連通子圖:連通子圖所能含有的最大結點數,如果再增加一個結點那麼這個子圖就不是連通圖了
(11) 生成樹:一個極小連通子圖,它含有圖中全部的頂點,但只有足以構成一顆樹的n-1 條邊,這樣的連通子圖就是連通圖的生成樹
其實就是透過一條路徑,能夠讓圖中所有的結點串連起來。在連通分量的圖中,我們就根據兩個連通分量生成了兩個最小生成樹。它們的 連通分量1 的生成樹的結點不一定非要是這種結構,我們可以讓 結點4 在 結點2 下,這取決於我們如何遍歷來產生這顆最小生成樹。
最上面我們的 圖a 的最小生成樹其實可以是 圖a-1 去掉那條紅色虛線。當然,也可以讓 結點4 也在 結點1 下面,同樣也取決於我們的程式要如何遍歷圖來產生什麼樣的樹。
是不是看完後暈頭轉向了?沒關係,這些術語我們在後面的學習中將會經常用到,而且這還不是最全面的。大家可以根據參考書目和其它學習資料來對圖的相關術語進行更深入的學習和理解。
圖的概念介紹得差不多了,大家可以消化消化再繼續學習後面的內容。這只是個開始,不少同學會不會覺得這玩意對比 樹 結構一下子又提升了很多。不用怕,在學習後面的知識後,即使你暫時還沒搞懂 圖 相關的內容,但你一定對 樹 結構的理解會更加深入了。為什麼呢?樹 其實就是沒有迴路的圖,它們的遍歷無外乎都是透過深度或廣度來實現的,只是圖更複雜一點而已。這下是不是感覺未來還是有點希望的啦?學習,往往是一個漸進的過程,當前的知識和過去的知識總會有所關聯的,先不用想太多,一步一步的踏實走下去吧!
推薦:《2021年PHP面試題大匯總(收藏)》《php影片教學》
以上是php中圖是什麼?如何才能進行儲存?的詳細內容。更多資訊請關注PHP中文網其他相關文章!
