本篇文章是mysql的進階學習，介紹一下mysql使用B 樹作為索引資料結構的原因，希望對大家有幫助！
索引提高查詢效率，就像我們看的書，想要直接翻到某一章，是不是不用一頁一頁的翻，只要看下目錄，根據目錄找到其所在的頁數即可。 【相關推薦：mysql影片教學】
在電腦中我們需要一種資料結構來儲存這個目錄，常見資料結構有雜湊表，二元查找樹，二元平衡樹(AVL)，紅黑樹，那為什麼Innodb和MyISAM選擇b 樹。
1. 雜湊表
雜湊表就是一個陣列 鍊錶，用下標0，1，2，3..... 表示其資料所在的位置。如果想要在雜湊表中存放數據，首先用對這個數據進行散列演算法（基本的就是取模運算），假如數組長度是13 ，進行模13之後是0-12，正好對應的數據的下標，如果計算出的下標一樣的，就會在下標位置跟上鍊錶。
缺點：
- 利用hash儲存需要將所有的資料檔案加入內存，比較消耗記憶體空間。
- hash的查找是等值查詢，速度很快，但是各個資料間沒有範圍規律，但在實際工作中更多的是範圍查詢，hash就不太合適了。
不能直接說mysql不使用雜湊表，而是要根據儲存引擎來決定的，Memory儲存引擎使用的就是雜湊表
# 2. 二元尋找樹
缺點：
- 如圖，極端情況可能會出現傾斜的問題，最後變成鍊錶結構。
- 造成樹節點過深，進而增加尋找的IO，而現在IO就是尋找的瓶頸
3. 二元平衡樹-AVL
為了保持樹的平衡，避免出現資料傾斜，需要進行旋轉操作，透過左旋或右旋最終保持最長子樹和最短子樹長度不能超過1，如果超過1就不是嚴格意義上AVL樹了
缺點：
#1.當資料量很大的時候，為了保持平衡，需要進行1-n次的旋轉，這個旋轉是比較浪費效能的，插入和刪除效率極低，查詢效率很高。
- 只有兩個分支，資料量大的時候樹的深度依然很深。
4. 紅黑樹
#最長子樹的不能超過最短子樹的2倍，透過變色和旋轉，在插入和查詢上做了平衡
紅黑樹是avl樹的變種，損失了部分查詢效能來提高插入效能。
缺點：
同樣是只有兩個分支，資料量大的時候深度還是會很深
#以上三種二元樹，隨著資料的增多，最終都會出現節點過多的情況，而且他們有且僅有2個分支，那麼IO的次數一樣很多.
##怎麼解決僅有2個分支而且深度過深，這就有了B樹，增加分支
5. B-Tree
首先不讀B減樹，讀B樹- 所有鍵值分佈在整棵樹中。
- 搜尋有可能在非葉子結點結束，在關鍵字全集內做一次查找，效能逼近二分查找。
- 每個結點最多擁有m個子樹。
- 根節點至少有2個子樹。
- 分支節點至少擁有m/2棵子樹(除根節點和葉子節點外都是分支節點)。
- 所有葉子節點都在同一層，每個節點最多可以有m-1個key,並且以升序排列
-
如上圖：（圖中只是畫出來一部分，實際上沒有限制的，不只p1,p2,p3）
每個節點佔用一個磁碟區塊，一個節點上有兩個升序排列的關鍵字和三個指向子樹根節點的指針，指針儲存的是子節點所在的磁碟區塊位址。兩個關鍵字分割成的三個範圍域對應三個指標指向的子樹的資料的範圍域。以根節點為例，關鍵字為16和34，p1指標指向的子樹的資料範圍小於16，p2指標指向的子樹的資料範圍為16-34，p3指標指向的子樹的資料範圍大於34 。
尋找關鍵字28的過程：
- 根據根節點找到磁碟區塊1，讀到記憶體中。 【第一次磁碟I/O操作】
- 比較關鍵字28在區間(16，34)，找到磁碟區塊1的指標p2。
- 根據p2指標找到磁碟區塊3，讀到記憶體。 【第二次磁碟I/O操作】
- 比較關鍵字28在區間(25，31)，找到磁碟區塊3的指標p2。
- 根據指標p2找到磁碟區塊8，讀到記憶體。 【第三次磁碟I/O操作】
- 在磁碟區塊8中的關鍵字清單中找到關鍵字28，結束。
缺點：
- 每個節點都有key，同時包含data，而每個頁儲存空間是有限的，如果data很大的話會導致每個節點能儲存的key的數量變小。
- 當儲存的資料量很大的時候會導致深度變大，增加查詢磁碟的io次數，進而影響查詢效能。
6. B 樹
B 樹是在B樹的基礎上所做的最佳化，變化如下：
- B樹每個節點可以包含更多的節點，這個做的原因有兩個，第一個原因是為了降低樹的高度，第二個原因是將資料範圍變成多個區間，區間越多，資料檢索越快。
- 非葉節點只儲存key，葉節點儲存key和資料。
- 葉子節點兩兩指標互相連接(符合磁碟預讀的特性)，順序查詢效能更高。
如上圖：
在B 樹上有兩個頭指針，一個指向根節點，另一個指向關鍵字的最小葉子節點，而且所有葉子節點(及資料節點)之間是一種鍊式環結構，因此可以對B 樹進行兩種查找運算：一種是對於主鍵的範圍查找和分頁查找，另一種是從根節點開始的隨機查找。
InnoDB和MyISAM中索引上的差異
1. InnoDB-主鍵索引
葉子節點儲存的是具體的行資料
2. InnoDB-非主鍵索引
非主鍵索引的葉子節點儲存的是主鍵值（所以查詢資料基本上要回表）
3. MyISAM
葉子節點儲存的是行資料的位址，額外需要一次尋址，多一次IO
總結：為什麼mysql使用的是B 樹
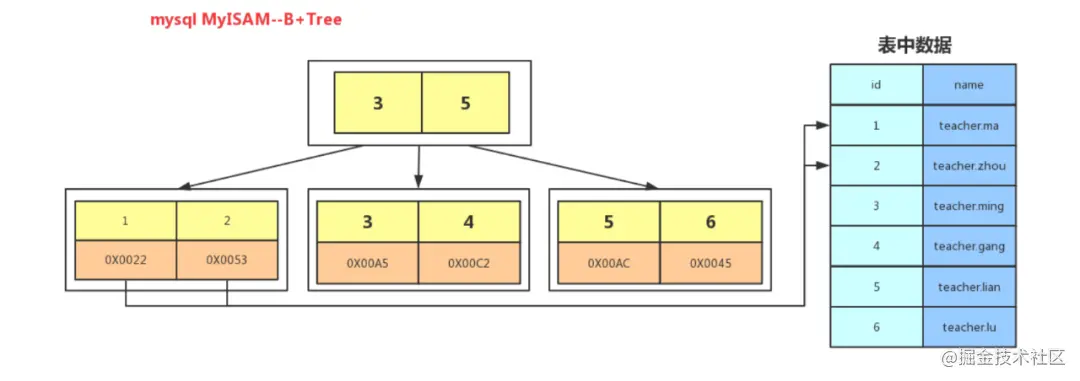
準確的表述：為什麼mysql的InnoDB和MyISAM儲存引擎的索引使用的是B 樹
hash表，等值查詢是很快的，但是不滿足常用的範圍查找且相鄰的兩個值之間沒有關係，而且hash比較消耗記憶體。
二元樹/平衡二元樹/紅黑樹等都是有且僅有2個分支，共性就是資料量大的時候樹的深度變深，增加IO的次數。
B樹會在節點上儲存數據，這樣一頁存放的key的數量就會減少，增加樹的深度。
B 樹中非葉子節點去除了數據，這樣就會增加一頁中key的數量，而且葉子節點之間是透過鍊錶相連，有利於範圍查找和分頁。
原文網址：https://juejin.cn/post/6994810803643744269
#作者：紀先生
#更多程式相關知識，請造訪：程式設計影片！ ！
以上是深入聊聊mysql索引為什麼採用B+樹結構的詳細內容。更多資訊請關注PHP中文網其他相關文章！
