本篇文章為大家帶來了關於python的相關知識，其中主要介紹了數據分析中異常值的相關問題，一般異常值的檢測方法有基於統計的方法，基於聚類別的方法，以及一些專門檢測異常值的方法等，以下對這些方法進行相關的介紹，希望對大家有幫助。
推薦學習：python學習教學
在機器學習中，異常檢測和處理是一個比較小的分支，或者說，是機器學習的一個副產物，因為在一般的預測問題中，模型通常是對整體樣本資料結構的一種表達方式，這種表達方式通常抓住的是整體樣本一般性的性質，而那些在這些性質上表現完全與整體樣本不一致的點，我們就稱其為異常點，通常異常點在預測問題中是不受開發者歡迎的，因為預測問題通產關注的是整體樣本的性質，而異常點的生成機制與整體樣本完全不一致，如果演算法對異常點敏感，那么生成的模型並不能對整體樣本有一個較好的表達，從而預測也會不準確。 從另一方面來說，異常點在某些場景下反而令分析者感到極大興趣，如疾病預測，通常健康人的身體指標在某些維度上是相似，如果一個人的身體指標出現了異常，那麼他的身體狀況在某些方面肯定發生了改變，當然這種改變並不一定是由疾病引起（通常被稱為噪音點），但異常的發生和檢測是疾病預測一個重要起始點。相似的場景也可以應用在信用欺詐，網路攻擊等等。
一般異常值的檢測方法有基於統計的方法，基於聚類的方法，以及一些專門檢測異常值的方法等，下面對這些方法進行相關的介紹。
如果使用pandas，我們可以直接使用describe()來觀察資料的統計性描述（只是粗略的觀察一些統計量），不過統計數據為連續型的，如下：
df.describe()
或簡單使用散佈圖也能很清晰的觀察到異常值的存在。如下所示：
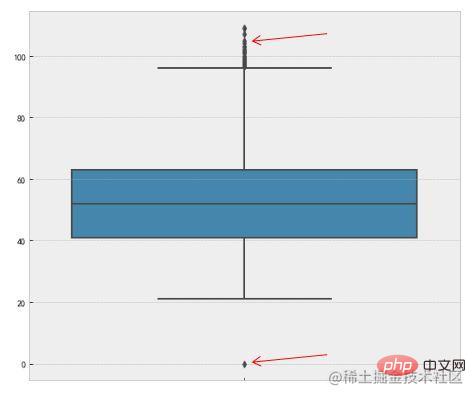
這個原則有個條件：資料需要服從常態分配。在3∂原則下，異常值如超過3倍標準差，那麼可以視為異常值。正負3∂的機率是99.7%，那麼距離平均值3∂之外的值出現的機率為P(|x-u| > 3∂) <= 0.003，屬於極個別的小機率事件。如果資料不服從常態分佈，也可以用遠離平均值的多少倍標準差來描述。
紅色箭頭所指是異常值。
這種方法是利用箱型圖的四分位數間距（IQR）對異常值進行檢測，也叫 Tukey's test。箱型圖的定義如下：
四分位數距(IQR)就是上四分位數與下四分位數的差值。而我們透過IQR的1.5倍為標準，規定：超過上四分位數 1.5倍IQR距離，或下四分位數-1.5倍IQR距離的點為異常值。下面是Python中的程式碼實現，主要使用了numpy的percentile方法。
Percentile = np.percentile(df['length'],[0,25,50,75,100]) IQR = Percentile[3] - Percentile[1] UpLimit = Percentile[3]+ageIQR*1.5 DownLimit = Percentile[1]-ageIQR*1.5
也可以使用seaborn的視覺化方法boxplot來實作：
f,ax=plt.subplots(figsize=(10,8)) sns.boxplot(y='length',data=df,ax=ax) plt.show()
機率分佈模型，並計算物件符合該模型的機率，把具有低機率的物件視為異常點。如果模型是簇的集合，則異常是不顯著屬於任何簇的物件；如果模型是迴歸時，異常是相對遠離預測值的物件。
離群點的機率定義：離群點是一個對象，關於資料的機率分佈模型，它具有低機率。這種情況的前提是必須知道資料集服從什麼分佈，如果估計錯誤就造成了重尾分佈。
例如特徵工程中的RobustScaler方法，在做資料特徵值縮放的時候，它會利用資料特徵的分位數分佈，將資料根據分位數劃分為多段，只取中間段來做縮放，例如只取25%分位數到75%分位數的資料做縮放。這樣減小了異常數據的影響。
優缺點：（1）有堅實的統計理論基礎，當存在充分的資料和所使用的檢定類型的知識時，這些檢定可能非常有效；（2）對於多元數據，可用的選擇少一些，並且對於高維度數據，這些檢測可能性很差。
統計方法是利用資料的分佈來觀察異常值，有些方法甚至需要一些分佈條件，而在實際中資料的分佈很難達到一些假設條件，在使用上有一定的限制。
確定資料集的有意義的鄰近性測量比確定它的統計分佈更容易。這種方法比統計方法更一般、更容易使用，因為一個物件的離群點得分由到它的k-最近鄰（KNN）的距離給定。
要注意的是：離群點分數對k的值高度敏感。如果k太小，則少量的鄰近離群點可能導致較低的離群點得分；如果K太大，則點數少於k的簇中所有的物件可能都成了離群點。為了使方案對於k的選取更具穩健性，可以使用k個最近鄰的平均距離。
優缺點：（1）簡單；（2）缺點：基於鄰近度的方法需要O(m2)時間，大資料集不適用；（3）該方法對參數的選擇也是敏感的；（4）不能處理具有不同密度區域的資料集，因為它使用全域閾值，不能考慮這種密度的變化。
從基於密度的觀點來說，離群點是在低密度區域的物件。基於密度的離群點檢測與基於鄰近度的離群點檢測密切相關，因為密度通常用鄰近度定義。 一種常用的定義密度的方法是，定義密度為到k個最近鄰的平均距離的倒數。如果該距離小，則密度高，反之亦然。 另一種密度定義是使用DBSCAN聚類演算法所使用的密度定義，即一個物件周圍的密度等於該物件指定距離d內物件的個數。
優缺點：（1）給出了物件是離群點的定量度量，並且即使資料具有不同的區域也能夠很好的處理；（2）與基於距離的方法一樣，這些方法必然具有O(m2)的時間複雜度。對於低維度資料使用特定的資料結構可以達到O(mlogm)；（3）參數選擇是困難的。雖然LOF演算法透過觀察不同的k值，然後取得最大離群點得分來處理該問題，但是，仍然需要選擇這些值的上下界。
基於聚類的離群點：一個物件是基於聚類的離群點，如果該物件不強屬於任何簇，那麼該對象屬於離群點。
離群點對初始聚類的影響：如果透過聚類檢測離群點，則由於離群點影響聚類，因此存在一個問題：結構是否有效。這也是k-means演算法的缺點，對離群點敏感。為了處理問題，可以使用以下方法：物件聚類，刪除離群點，物件再次聚類（這個不能保證產生最優結果）。
優缺點：（1）基於線性和接近線性複雜度（k均值）的聚類技術來發現離群點可能是高度有效的；（2）簇的定義通常是離群點的補，因此可能同時發現簇和離群點；（3）產生的離群點集和它們的得分可能非常依賴所用的簇的個數和數據中離群點的存在性； （4）聚類演算法產生的簇的品質對此演算法產生的離群點的質量影響非常大。
其實以上說到聚類方法的本意是無監督分類，並不是為了尋找離群點的，只是恰好它的功能可以實現離群點的偵測，算是衍生的功能。
除了以上提及的方法，還有兩個專門用於檢測異常點的方法比較常用：One Class SVM和Isolation Forest，詳細內容不進行深入研究。
偵測到了異常值，我們需要對其進行一定的處理。而一般異常值的處理方法可大致分為以下幾種：
是否要刪除異常值可依實際情況考慮。因為有些模型對異常值不很敏感，即使有異常值也不影響模型效果，但是有些模型例如邏輯迴歸LR對異常值很敏感，如果不進行處理，可能會出現過擬合等非常差的效果。
以上是對異常值偵測和處理方法的總和。
透過一些檢測方法我們可以找到異常值，但所得結果並不是絕對正確的，具體情況還需自己根據業務的理解加以判斷。同樣，對於異常值如何處理，是該刪除，修正，還是不處理也需結合實際情況考慮，沒有固定的。
推薦學習：python教學
#以上是Python資料異常值檢測與處理（實例詳解）的詳細內容。更多資訊請關注PHP中文網其他相關文章！
