javascript怎麼求素數-js教程-PHP中文網

javascript怎麼求素數

青灯夜游

發布： 2022-09-20 11:59:20

原創

4325 人瀏覽過

求質數的方法：1、遍歷1~n區間中的所有自然數給n來除，若餘數為0則表示該數n不是素數，否則就是質數，語法「for(i=2 ;i

javascript怎麼求素數

本教學操作環境：windows7系統、javascript1.8.5版、Dell G3電腦。

素數的概念

素數又叫質數，質數是指在大於1的自然數中，除了1和它本身以外，不能被其他自然數整除的數。

100以內的質數：2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71 、73、79、83、89、97，共25個。

JavaScript判定質數的四個方法

1、質數只能由1、自身整除

素數只能被1和自身整除，所以遍歷（1，n）開區間中的所有自然數給n來除，若存在整除，即餘數為0，則表示該數n不是素數，否則就是素數。

function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  for (let i = 2; i <p>但是這種演算法的複雜度為O(n)</p><h3 id="%E7%B4%A0%E6%95%B0%E5%B9%B3%E6%96%B9%E6%A0%B9%E8%8C%83%E5%9B%B4"><strong>2、質數平方根範圍</strong></h3><p>假設n不是質數，則n除了可以被1和n整除外，還可以被i、j整除，即n / i = j...0，例如15不是質數，15 / 3 = 5，例如35不是質數，35 / 5 = 7，此時i,j必然分別處於(1, Math.sqrt(n)]和[Math.sqrt(n), n） 之中，如Math.sqrt(15) ≈ 3.8，則3處於（1，3.8]， 5處於[3.8, 15）。如Math.sqrt(4) = 2，則2處於(1,2]中，也處於[2,4)中。 </p><pre class="brush:php;toolbar:false">function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  for (let i = 2; i <p>此時演算法複雜度為O（sqrt(n)）</p><h3 id="%E7%B4%A0%E6%95%B0%E4%B8%8D%E8%83%BD%E6%98%AF%E9%99%A4%E4%BA%862%E5%A4%96%E7%9A%84%E5%81%B6%E6%95%B0"><strong>#3、素數不能非2的其他偶數</strong></h3><p>除了2，所有偶數都不是質數</p><p><img src="https://img.php.cn/upload/image/644/149/762/1663645614907138.png" title="1663645614907138.png" alt="javascript怎麼求素數"></p><pre class="brush:php;toolbar:false">function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  if (n % 2 === 0) {
    return false;
  }
 
  for (let i = 3; i <p>for迴圈中n，只能為上圖淺藍色部分。 </p><p>因此上面演算法減少了一半的循環，時間複雜度為O（sqrt(n) / 2） </p><p>需要注意的是，本演算法的程式碼不能將n % 2 == = 0 的判斷條件加入迴圈中，如下程式碼有漏洞</p><pre class="brush:php;toolbar:false">function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  for (let i = 3; i <p>此時4、6、8都會被判定為質數。 </p><p>漏洞形成的原因是，for迴圈的迴圈條件i </p><p>此演算法只能保證循環條件   i = i^2 = 9 時。 </p><h3 id="%E5%A4%A7%E4%BA%8E%E7%AD%89%E4%BA%8E5%E7%9A%84%E7%B4%A0%E6%95%B0%E4%B8%80%E5%AE%9A%E5%92%8C6%E7%9A%84%E5%80%8D%E6%95%B0%E7%9B%B8%E9%82%BB"><strong>4、大於等於5的質數一定和6的倍數相鄰</strong></h3><p>#大於等於5的質數一定和6的倍數相鄰</p><p> （注意這句話不等價於：<span style="text-decoration:line-through;">和6的倍數相鄰的數一定是大於5的質數</span>，該結論不成立。）</p><p><img src="https://img.php.cn/upload/image/346/360/896/166364562667908javascript%E6%80%8E%E9%BA%BC%E6%B1%82%E7%B4%A0%E6%95%B8" title="166364562667908javascript怎麼求素數" alt="javascript怎麼求素數"></p><p>如上圖中，將大於等於5的數分為了：6y-1、6y、6y 1、6y 2、6y 3、6y 4（y>=1）</p><p>#其中，6y、6y 2 、6y 3、6y 4都不可能是質數，只有6y-1和6y 1<strong><span   style="max-width:90%">可能</span></strong>是質數。 </p><p>另外，6y-1（y>=1）和 6y 5 （y>=0）等價。 </p><p>所以，我們可以將n不為6y-1（或6y 5）和6y 1的數直接排除，排除方法為，</p><pre class="brush:js;toolbar:false">  if (n % 6 !== 1 && n % 6 !== 5) {
    return false;
  }

登入後複製

下面要剔除6y-1（或6y 5）和6y 1中的非素數，

  for (let i = 5; i <= Math.sqrt(n); i += 6) {
    if (n % i === 0 || n % (i + 2) === 0) {
      return false;
    }
  }

登入後複製

這裡大家比較疑惑的可能有兩點：

for循環i自增為啥是6
for迴圈中質數判定的條件為啥是n % i === 0 || n % (i 2) === 0

javascript怎麼求素數

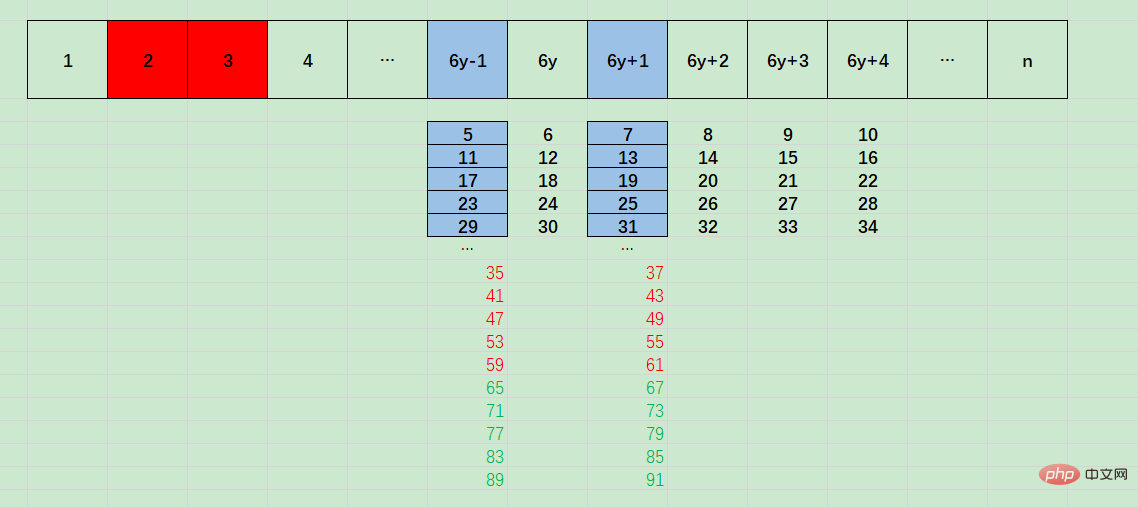
#我們看上面圖解，可以發現，6y-1，是基數為5，差值為6的等差數列，即5 6x :

对于 5 + 6x 而言，如果x为5的倍数（5 * z），则5 + 6x = 5 + 6 * 5 * z = 5 *（1+6z）,则此时5 + 6x可以被5整除。
5 + 6x 还可以转化为 5 + 6 + 6 * (x-1) = 11 + 6(x-1)，则只要x-1为11的倍数，则5 + 6x可以被11整除，
5 + 6x 还可以转化为 5 + 12 + 6 * (x-2) = 17 + 6(x-2)，则只要x-2为17的倍数，则5 + 6x可以被17整除
......

6y+1，是基数为7，差值为6的等差数列，即 7 + 6x :

对于 7 + 6x 而言，如果x为7的倍数（7 * z），则7 + 6x = 7 + 6 * 7 * z = 7 *（1+6z）,则此时7 + 6x可以被7整除。
7 + 6x 还可以转化为 7 + 6 + 6 * (x-1) = 13 + 6(x-1)，则只要x-1为13的倍数，则7 + 6x可以被13整除，
7 + 6x 还可以转化为 7 + 12 + 6 * (x-2) = 19 + 6(x-2)，则只要x-2为19的倍数，则7 + 6x可以被19整除，
......

所以6y-1和6y+1可能整除的数自增量为6，这是for循环i自增为啥是 6的原因

且6y-1和6y+1的整除数基数为5和7，相差为2，这是for循环中素数判定的条件为啥是 n % i === 0 || n % (i+2) === 0的原因

function isPrime(n) {
  n = parseInt(n);
 
  if (n <= 3) {
    return n > 1;
  }
 
  if (n % 6 !== 1 && n % 6 !== 5) {
    return false;
  }
 
  for (let i = 5; i <= Math.sqrt(n); i += 6) {
    if (n % i === 0 || n % (i + 2) === 0) {
      return false;
    }
  }
 
  return true;
}

登入後複製

此时时间复杂度为 O（sqrt(n) / 3）

【相关推荐：javascript视频教程、编程基础视频】

以上是javascript怎麼求素數的詳細內容。更多資訊請關注PHP中文網其他相關文章！