PNAS最新研究：81%解題率，神經網路 Codex 推開高等數學世界大門

近日，一項新研究發佈於PNAS，再次刷新了神經網路的能力。這次神經網路被用來解決了高等數學題，而且還是麻省理工數學課程難度的數學題！

在這項新研究中，研究團隊證明了OpenAI 的Codex 模型可以進行程式合成從而解決大規模的數學問題，並透過小樣本學習自動解決資料集中81%的數學課程問題，並且Codex 在這些任務的表現上達到了人類水平。

原文連結：https://www.pnas.org/doi/10.1073/pnas.2123433119

#這項研究的出現，顛覆了人們普遍認為神經網路無法解決高等數學問題的共識。研究團隊指出，Codex 之所以能做到實現這樣的能力，正是因為團隊進行了一大創新，過去那些不成功的研究只使用了基於文本的預訓練，而此次現身的Codex 神經網路不僅要基於文字進行預訓練，並且還對程式碼進行了微調。

研究的問題資料集選用來自MIT 的六門數學課程和哥倫比亞大學的數學課程，從七門課程中隨機抽取25 個問題：MIT的單變量微積分、多變量微積分、微分方程、機率與統計概論、線性代數和計算機科學數學和哥倫比亞大學的COMS3251 計算線性代數。

同時，研究團隊使用了一個用於評估數學推理的最新高級數學問題基準MATH，用MATH 來檢測OpenAI Codex 的能力，MATH 從6大數學板塊：初級代數，代數，計數和機率，中級代數，數論，和初級微積分中各抽取15個問題。

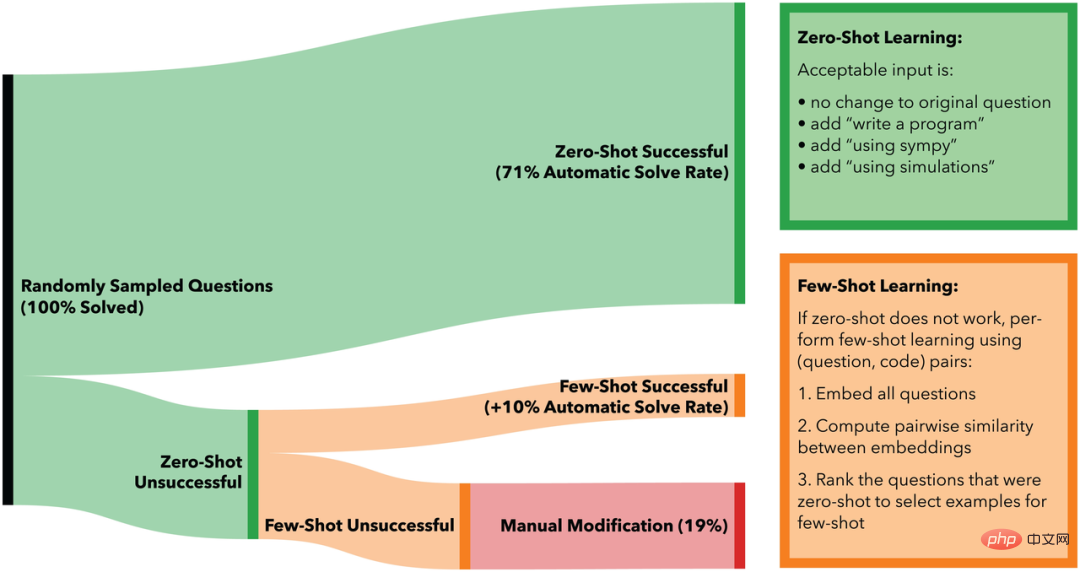
圖註：研究中使用的課程問題資料集與MATH基準測驗

研究顯示，Codex 解決了問題資料集和MATH 資料集中的265 個問題，其中有213 個是自動解決的。

1 創新何所在

在Transformer 發布後，基於Transformer 的語言模型在各種自然語言處理(NLP) 任務，包括在零樣本和少樣本語言任務中取得了巨大成功。但因為 Transformer 僅在文字上進行了預訓練，所以這些模型基本上無法解決數學問題，GPT-3就是一個典型例子。

後來，透過小樣本學習（few-shot learning）和思維鏈(Chain-of-thought， CoT) 提示，GPT-3 的數學推理能力得到了提升；然而，在沒有程式碼的情況下，即便有小樣本學習和CoT 提示， GPT-3 在大學層級數學問題和MATH 基準測試中仍然無能為力。

過去關於解數學題的研究，可能在相對簡單的數學層次上有一定成績。舉個例子，基於協同訓練輸出來驗證或預測表達式樹的技術，例如MAWPS 和Math23k，能夠以超過81% 的準確率解決小學級別的數學問題，但是其不能解決高中、奧林匹克數學或大學難度的課程。協同訓練與圖神經網路 (GNN) 結合以預測算術表達式樹，能夠以高達 95% 的準確率解決機器學習中的大學程度問題。但是這項工作也僅限於數字答案，並且產生了過擬合，不能推廣到其他課程。

而這項工作的最大創新點之一就是，不僅對Codex 這種Transformer 模型進行了文字上的預訓練，還在程式碼上進行了微調，使得其可以產生大規模解決數學問題的程式。

#

研究團隊從資料集中隨機選擇不需要輸入影像或證明的問題樣本來進行測試。其中，僅對文本進行預訓練的語言模型 (GPT-3 text-davinci-002) 僅自動解決了課程問題中的18%和 MATH基準測試問題中的25.5%。

相比之下，使用零樣本學習和對文字進行預訓練並在程式碼上進行微調的神經網路（OpenAI Codex code-davinci-002）合成的程式可以自動解決課程問題中的71%和MATH 基準測試問題中的72.2%。

而使用相同的神經網路 Codex 再加上少樣本學習，便可自動解決課程中81%的問題和 MATH 基準測試中81.1%的問題。而其餘模型無法自動解決的19%的課程問題和18.9%的MATH基準問題，最後透過手動提示解決。

小樣本學習方式的補充，則是這項研究的第二大創新點。從上圖可以看出，當零樣本學習無法解答問題時，便會使用（問題，程式碼）對（pair）執行小樣本學習：

1） 使用OpenAI的text-similarity-babbage-001 嵌入引擎嵌入所有問題；

2） 使用嵌入的餘弦相似度從其課程中計算與未解決問題最相似的已解決問題；

3） 將最相似的問題及其對應的程式碼作為小樣本問題的範例。

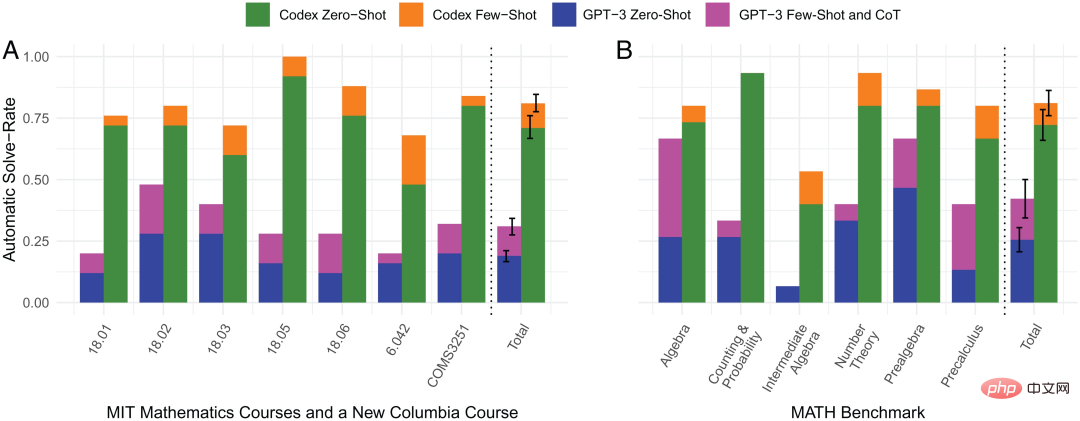
圖註：4種方式的自動解題率比較

#上圖分別是Codex的零樣本學習、小樣本學習和GPT-3的零樣本學習、小樣本學習4種方式的自動解題率比較。圖上可以看出，橘色條狀所代表的小樣本學習 Codex 在自動解題率上的優秀表現，基本上在每個數學領域上的表現都強於其他3種方式。

這項研究的第三大創新點，便是提供了一條解決數學問題和解釋為何如此解答的管道，下圖展示了MIT 5門數學課程中管道的執行流程。

以18.01 單變數微積分問題為例，給定一個問題和自動產生的前綴“使用SymPy”，Codex 被提示並輸出一個程序。運行程式會產生正確答案的方程式。然後，程式會自動提示再次輸入 Codex，從而產生產生的程式碼解釋。

2 問題解決之後

除了解決數學問題和解釋答案，Codex 也被用來為每門課程產生新問題。

為了評估生成的問題水平，團隊在參加過這些課程或同水平課程的MIT學生中做了調查，主要是比較機器生成的問題和人工編寫問題的質量和難度。

在MIT的6門課程中，每門選擇5個人工編寫問題和5個模型生成問題混合起來並且隨機呈現。對於 60 個問題中的每一個問題，參與調查的學生都需要回答 3 個調查問題：

1）你認為這個問題是手動寫的還是機器產生的？

2）你認為這個問題適合還是不適合特定課程？

3 ) 在 1（最簡單）和 5（最難）之間，你認為這個問題的難度等級是多少？

#

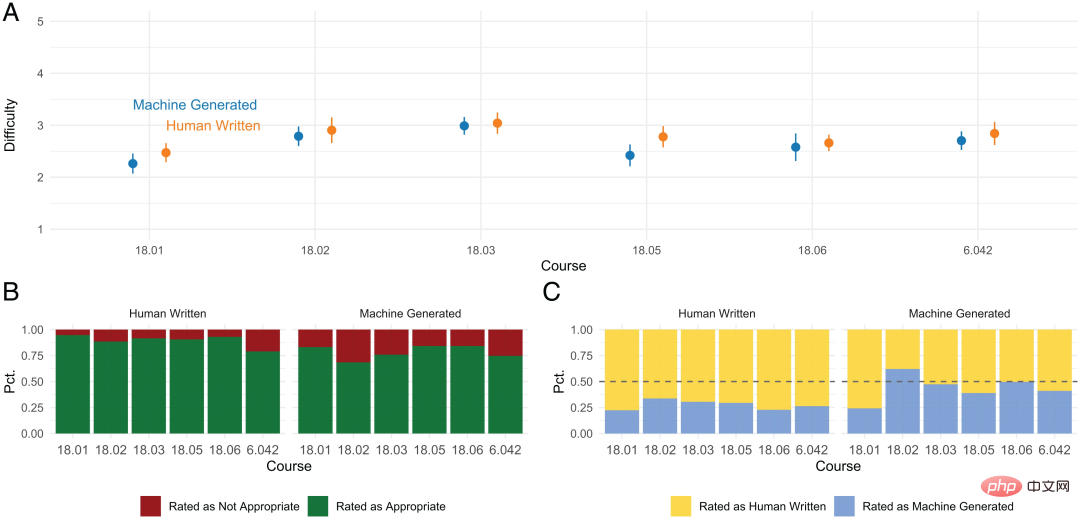
在收回的問卷中，學生調查結果總結如下：

• 機生成和手動編寫的問題難度相似。
• 人工編寫的問題比機器產生的問題更適合課程。
• 人工寫的答案很難被辨識錯，而機器產生的問題被學生認為既可能是機器產生的，也可能是人工寫的。

機器產生的問題已經能讓學生無法辨別，說明Codex 在產生新內容方面已達到了人類的表現水準。

但是，模型也有無法解決的問題，例如，如果問題以圖像或其他非文字形式出現，它就無法回答；帶有需要證明的解決方案的問題，或是計算上難以解決的問題，例如分解非常大的質數，模型也無法解決。不過，最後一種問題也不應該出現在任何數學課程作業中，因為就算是真人學生也沒辦法回答。

以上是PNAS最新研究：81%解題率，神經網路 Codex 推開高等數學世界大門的詳細內容。更多資訊請關注PHP中文網其他相關文章！