不得不说，科学家们最近都在痴迷给AI补数学课了。
这不，脸书团队也来凑热闹，提出了一种新模型，能完全自动化论证定理，并显著优于SOTA。
要知道，随着数学定理愈加复杂，之后再仅凭人力来论证定理只会变得更加困难。
因此，用计算机论证数学定理已经成为一个研究焦点。
此前OpenAI也提出过专攻这一方向的模型GPT-f，它能论证Metamath中56%的问题。
而这次提出的最新方法，能将这一数字提升到82.6%。
与此同时，研究人员表示该方法使用的时间还更短，与GPT-f相比可以将计算消耗缩减到原本的十分之一。
难道说这一次AI大战数学，是要成功了?
本文提出的方法为一种基于Transformer的在线训练程序。
大致可以分为三步：
第一、在数学证明库中预训练;
第二、在有监督数据集上微调策略模型;
第三、在线训练策略模型和判断模型。
具体来看是利用一种搜索算法，让模型在已有的数学证明库中学习，然后去推广证明更多的问题。
其中数学证明库包括3种，分别是Metamath、Lean和自研的一种证明环境。
这些证明库简单来说，就是把普通数学语言转换成近似于编程语言的形式。
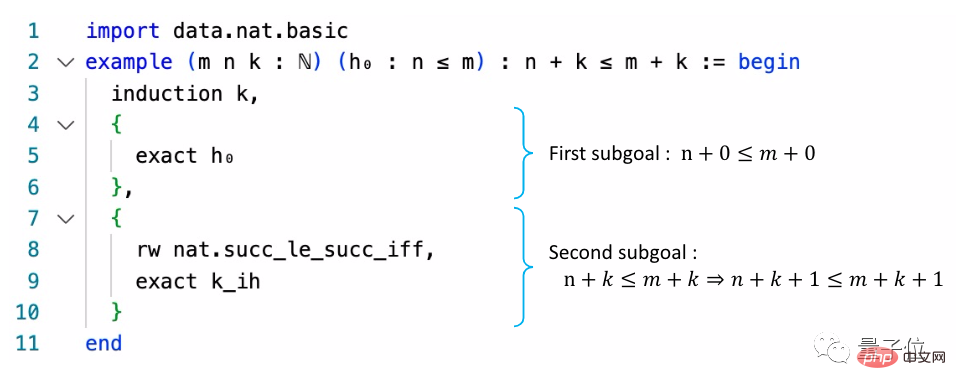
Metamath的主库是set.mm，包含基于ZFC集合论的约38000个证明。
Lean更为人熟知的，是微软那个可以参加IMO赛事的AI算法。Lean库就是为了教会同名算法所有的本科数学知识，并让它学会证明这些定理。
这项研究的主要目标，是为了构建一个证明器，让它可以自动生成一系列合适的策略去论证问题。
为此，研究人员提出了一个基于MCTS的非平衡超图证明搜索算法。
MCTS译为蒙特卡洛树搜索，常用于解决博弈树问题，它因为AlphaGo所被人熟知。
它的运行过程，就是通过在搜索空间中随机抽样来找寻有希望的动作，然后根据这个动作来扩展搜索树。
本项研究采用的思路类似于此。
搜索证明过程从目标g开始，向下搜索方法，逐步发展成一个超图(Hypergraph)。
当出现一个分支下出现空集时，就意味着找到了一个最优证明。
最后，在反向传播过程中，记下超树的节点值和总操作次数。
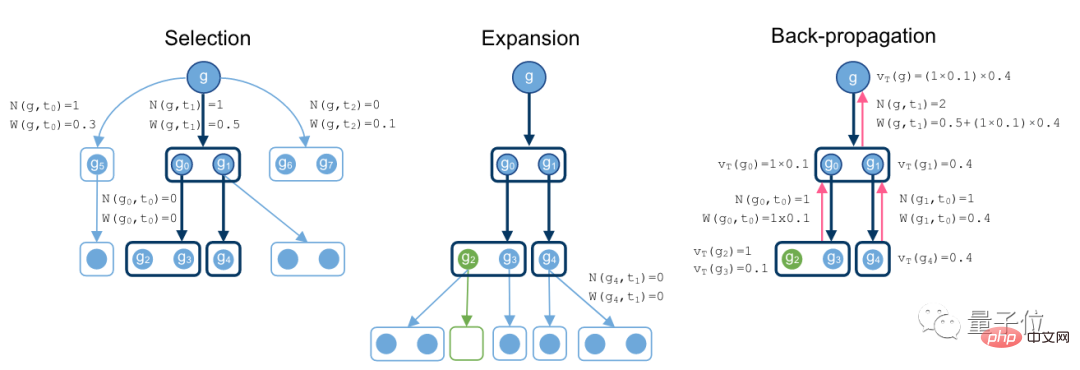
在这个环节中，研究人员假设了一个策略模型和一个判断模型。
策略模型允许判断模型进行抽样，判断模型可以评估当前策略找到证明方法的能力。
整个搜索算法，就以如上两个模型作为参照。
而这两个模型都是Transformer模型，且权值共享。
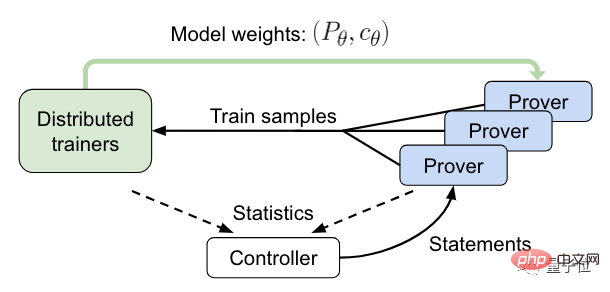
接下来，就到了在线训练的阶段。
这个过程中，控制器会将语句发送给异步HTPS验证，并收集训练和证明数据。
然后验证器会将训练样本发送给分布式训练器，并定期同步其模型副本。
在测试环节，研究人员将HTPS与GPT-f进行了比较。
后者是OpenAI此前提出的数学定理推理模型，同样基于Transformer。
结果表明，在线训练后的模型可以证明Metamath中82%的问题，远超GPT-f此前56.5%的记录。
在Lean库中，这一模型可以证明其中43%的定理，比SOTA提高了38%，以下是该模型证明出的IMO试题。
不过目前它还不是十全十美。
比如在如下这道题中，它并没有用最简便的办法解出题目，研究人员表示这是因为注释中出现了错误。
用電腦論證數學問題，四色定理的證明就是最為人熟知的例子之一。
四色定理是近代數學三大難題之一，它提出「任何一張地圖只用四種顏色就能使具有共同邊界的國家，著上不同的顏色」。
由於這定理的論證需要大量計算，在它被提出後100年內，都沒有人能完全論證。
直到1976年，在美國伊利諾大學兩台電腦上，經過1200小時、100億次判斷後，終於可以論證任何一張地圖都只需要4種顏色來標記，由此也轟動了整個數學界。
加上之隨著數學問題愈加複雜，用人力來檢驗定理是否正確也變得更加困難。
近來，AI界也把目光逐步聚焦在數學問題上。
2020年，OpenAI推出數學定理推理模型GPT-f，可用來自動定理證明。
此方法可完成測試集中56.5%的證明，超過當時SOTA模型MetaGen-IL30%以上。
同年，微軟也發布了可以做出IMO試題的Lean，這意味著AI能做出沒見過的題目了。
去年，OpenAI給GPT-3加上驗證器後，做數學題效果明顯好於先前微調的辦法，可以達到小學生90%的水準。
今年1月，來自MIT 哈佛 哥倫比亞大學 滑鐵盧大學的一項聯合研究表明，他們提出的模型可以做高數了。
總之，科學家們正在努力讓AI這個偏科生變得文理雙全。
以上是AI能證明數學資料庫中82%的問題了，新SOTA已達成，還是基於Transformer的詳細內容。更多資訊請關注PHP中文網其他相關文章！
