人類反超 AI：DeepMind 用 AI 打破矩陣乘法計算速度 50 年記錄一週後，數學家再次刷新

10 月 5 日，AlphaTensor 橫空出世，DeepMind 宣布其解決了數學領域 50 年來一個懸而未決的數學演算法問題，即矩陣乘法。 AlphaTensor 成為第一個用於為矩陣乘法等數學問題發現新穎、高效且可證明正確的演算法的 AI 系統。論文《Discovering faster matrix multiplication algorithms with reinforcement learning》也登上了 Nature 封面。

然而，AlphaTensor 的記錄只維持了一周，便被人類數學家打破了。

來自奧地利林茨約翰·開普勒大學的研究人員 Manuel Kauers 和 Jakob Moosbauer 在最新工作中表示，他們已經打破 AlphaTensor 的矩陣乘法記錄。他們開發了一種以 95 步執行 5×5 矩陣乘法的方法，比 AlphaTensor 的 96 步記錄少了一步，此前的記錄為 98 步。論文預印版於 10 月 13 日發佈在 arxiv 上。

#論文網址：https://arxiv.org/abs/2210.04045

論文標題中的「FBHHRBNRSSSHK」其實就是DeepMind 論文所有作者姓氏的首字母組合，這種命名方式也是很有趣了：

數學問題的探索永無止境，如作者所說，DeepMind 演算法方案「still not the end of the story」。不過，他們這次的突破是站在巨人也就是 AI 的肩膀上，作者表示，其解決方案是在 DeepMind 方案的基礎上應用一系列的轉換，從而消除了一步乘法計算。

1 前進 2 步驟的 AlphaTensor

我們先來簡單回顧一下 AlphaTensor 的成績。

電腦科學中許多數學任務都是透過矩陣乘法來處理的，例如機器學習、電腦圖形的創建，各種模擬或資料壓縮。而電腦計算乘法的速度要遠遠慢於加法，因此，即使矩陣乘法的效率提升得很小，也會產生巨大影響，幾十年來，數學家們一直在尋找更有效的矩陣乘法演算法。

1969 年，德國數學家 Volker Strassen 開發了一種演算法，首次將 4×4 矩陣乘法的解算從 64 步減少到 49 步，震動了數學界。

而 Deepmind 這次發布的 AI 系統 AlphaTensor，發現了比 Strassen 演算法更快的新演算法。 Demis Hassabis 稱，新演算法具備在每天數萬億次計算中將效率提高 10% ~ 20% 的潛力。

AlphaTensor 是從遊戲到數學的飛躍，它基於 2018 年 Deepmind 發布的通用棋盤遊戲 AI 系統 AlphaZero。為了訓練 AlphaTensor，Deepmind 研究團隊將矩陣乘法問題轉化成 3D 棋盤遊戲，每一步都會產生新演算法的構建塊。 AlphaTensor 每次都會在數萬次移動中進行選擇，以盡可能少的步驟產生新演算法而獲得獎勵。 Deepmind 稱之為「張量遊戲」。

在 5×5 的輸入矩陣中，AlphaTensor 獨立發現了 Strassen 演算法和其他已知的演算法。並且，它也開發了比舊演算法更有效的新演算法。

例如，5×5 矩陣乘法（n=4）以前要計算80 步，而AlphaTensor 新演算法只需76 步；當n=5 時，AlphaTensor 將求解從原來的98 步減少到96 步。 4×4 矩陣乘法由 Strassen 減少到 49 步，AlphaTensor 則將其最佳化為 47 步。這樣的效率是由 AlphaTensor 產生的 70 多個矩陣乘法的演算法實現的。

#

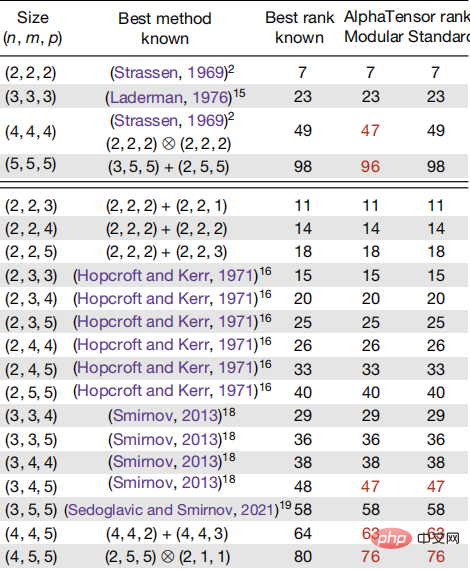
圖註：AlphaTensor 發現的演算法複雜性與已知矩陣乘法演算法比較

此外，AlphaTensor 還可開發特定硬體的演算法，用於機器學習。據說目前運行速度比Google TPU 和英偉達 V100 上的演算法快 20%。

自主調整乘法演算法以適應硬體的方法對人類來說很困難，所以AlphaTensor 對Strassen 演算法的改進創造了4×4 矩陣乘法的新上限，是AI 進步為其他學科提供助力的一大證明。它還表明，原本為傳統遊戲開發的 AlphaZero 系統可以解決領域之外的數學問題。

2 人類再往前1 步

#在Manuel Kauers 和Jakob Moosbauer 的最新研究中，他們主要有兩個新發現，一是對於4×4 矩陣，他們提出了另一種47 步乘法的求解演算法，但不同於先前的解；二是對於5×5 矩陣，他們首次提出了一個需要95 步乘法的方案。

在這篇文章中，作者簡單展示了這兩個矩陣乘法的方案，不久後將發表正式論文，更詳細地介紹求解演算法的搜尋技術。

4 × 4 矩陣的新方案共包含47 次乘法，如下：

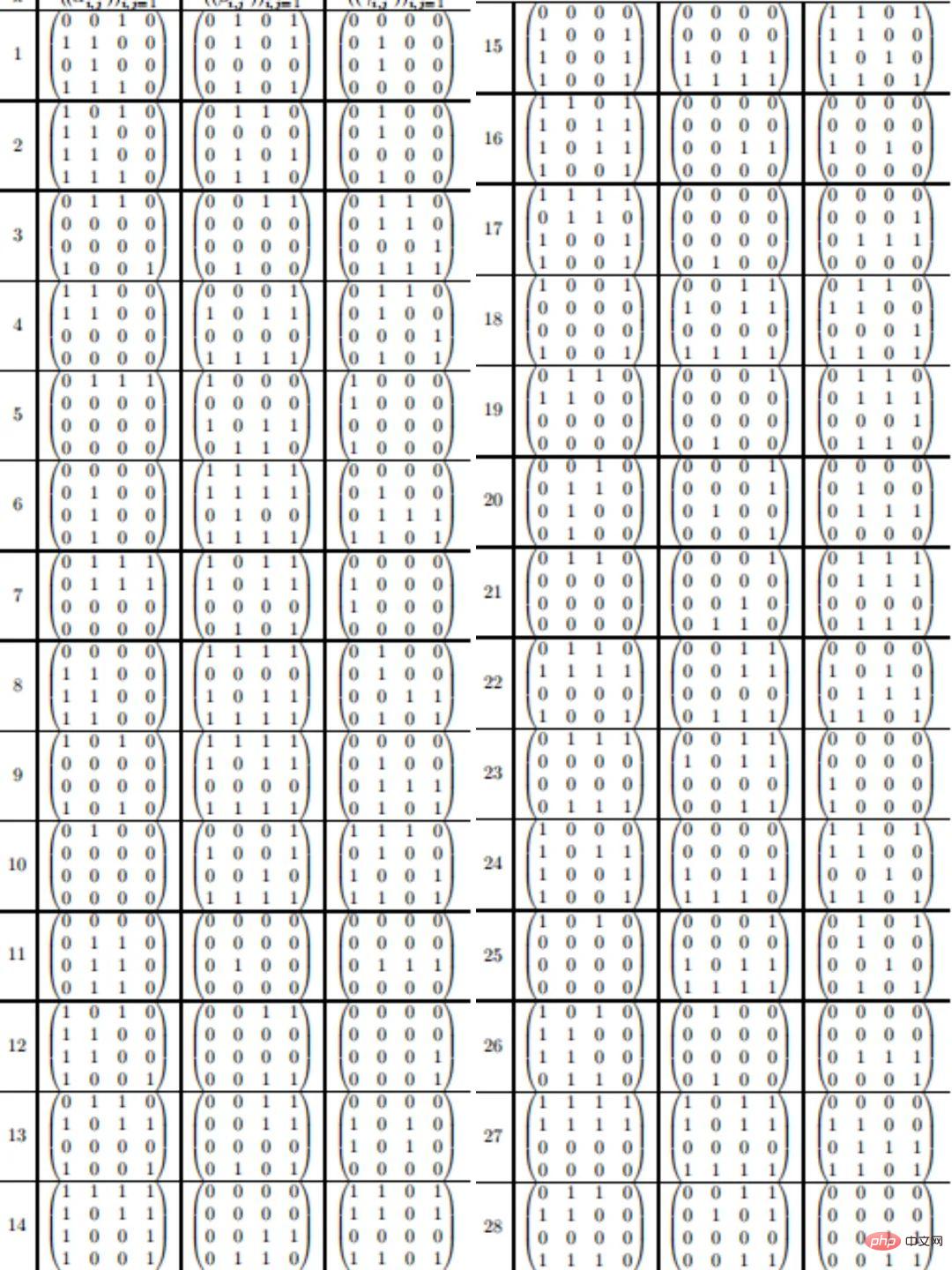
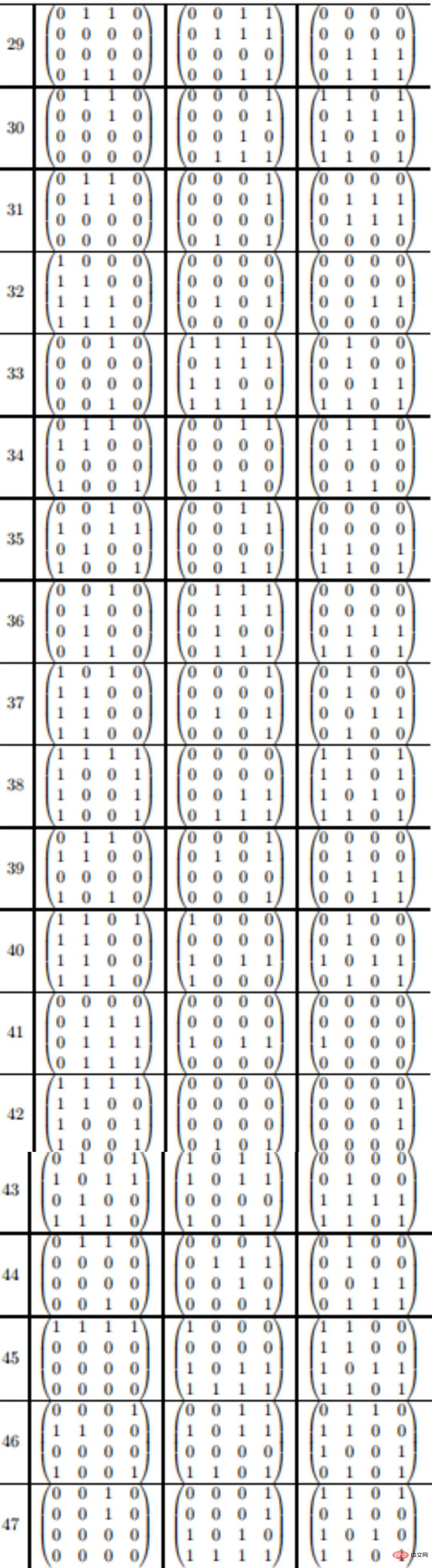
5 ×5 矩陣（n=5）的95 步驟乘法方案如下：

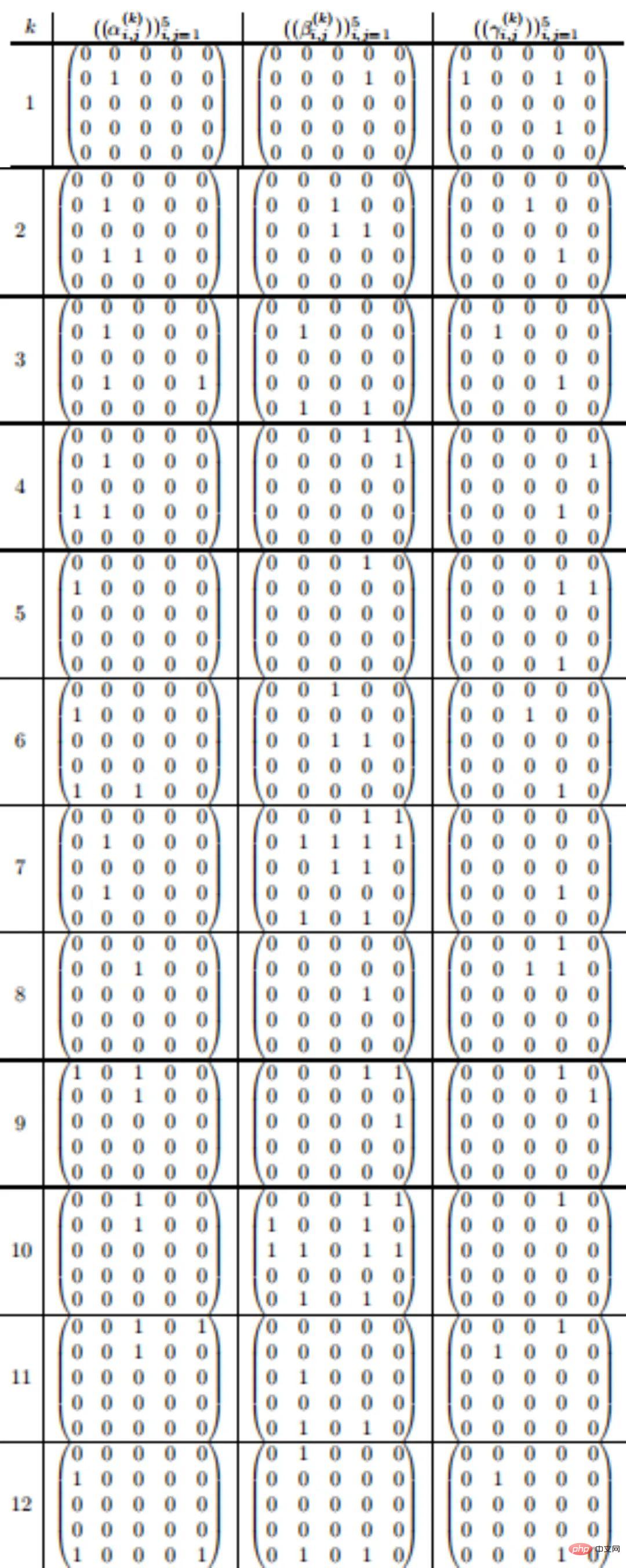
考慮到GPU 每天要進行萬億次矩陣計算，所以從98 步到96 步以及從96步到95 步這樣看起來很小的漸進式改進，實際上能大幅提升運算效率，可以讓AI 應用程式在現有硬體上運行得更快。

作者介紹：

Manuel Kauers，由林茨約翰內斯開普勒大學的代數教授，該大學代數研究所的負責人。其研究興趣為計算機代數、符號求和和積分、特殊函數恆等式等。

Jakob Moosbauer，在林茨約翰內斯開普勒大學代數研究所博士生。

以上是人類反超 AI：DeepMind 用 AI 打破矩陣乘法計算速度 50 年記錄一週後，數學家再次刷新的詳細內容。更多資訊請關注PHP中文網其他相關文章！