我是如何從頭開始寫一篇頂尖論文的
最近完成了一篇很滿意的論文,不僅整個過程愉快、回味無窮,而且真正做到了「學術有影響,工業有產出」。我相信這篇文章會改變差分隱私(differential privacy;DP)深度學習的典範。
因為這次經驗實在太過「巧」了(過程充滿巧合、結論極其巧妙),在此和同學們分享一下自己從觀察-->構思-->實證-- >理論-->大規模實驗的完整流程。本文我會盡量保持 lightweight,不涉及過多技術細節。

論文地址:arxiv.org/abs/2206.07136
與paper 展現的順序不同,paper 有時會刻意將結論放在開頭吸引讀者,或先介紹簡化後的定理而將完整的定理放附錄;而本文我想將我的經驗按時間順序寫下(也就是流水帳), 例如把走過的彎路和研究中突發的狀況寫出來,以供剛踏上科研之路的同學參考。
一、文獻閱讀
事情的起源是史丹佛的一篇論文,現在已經錄了ICLR:

論文網址:https://arxiv.org/abs/2110.05679
文章寫的非常好,總結起來有三個主要貢獻:
#1. 在NLP 任務中,DP 模型的accuracy 非常高,鼓勵了privacy 在語言模型的應用。 (與之相對的是CV 中DP 會產生非常大的accuracy 惡化,例如CIFAR10 目前DP 限制下不用預訓練只有80% accuracy,而不考慮DP 可以輕鬆達到95%;ImageNet 當時最好的DP accuracy 不到50%。)
2. 在語言模型上,模型越大,效能會越好。例如 GPT2 從 4 億參數到 8 億參數效能提升很明顯,也取得了許多 SOTA。 (但在CV 和推薦系統中,很多時候更大的模型性能會很差,甚至接近random guess。例如CIFAR10 的DP best accuracy 先前是由四層CNN 得到的,而非ResNet。)
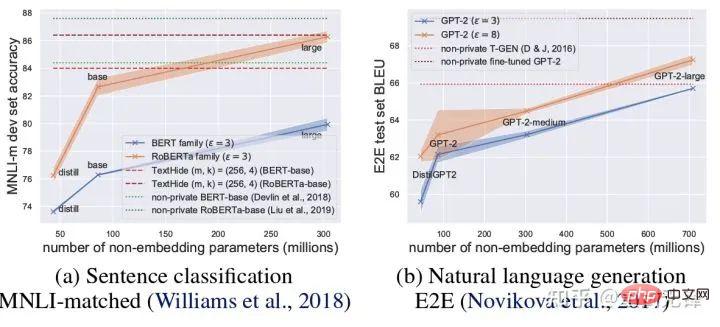
NLP 任務中DP 模型越大表現越好[Xuechen et al. 2021]
3. 在多個任務上取得SOTA 的超參數是一致的:都是clipping threshold 要設定的夠小,而且learning rate 需要大一些。 (先前所有文章都是一個任務調一個clipping threshold,費時費力,並沒有出現過像這篇這樣一個clipping threshold=0.1 貫穿所有任務,表現還這麼好。)
#以上總結是我讀完paper 瞬間理解的,其中括號內的內容並非來自這篇paper,而是以往許多閱讀產生的印象。這有賴於長期的閱讀累積和高度的概括能力,才能快速聯想和對比出來。
事實上,許多同學做文章起步難恰恰就在於看一篇文章只能看到一篇文章的內容,無法和整個領域的知識點形成網絡、產生聯想。這一方面由於剛入門的同學閱讀量不夠,尚未掌握足夠的知識點。尤其是長期從老師手中拿課題,不自己獨立 propose 的同學,容易有這個問題。另一方面則是閱讀量雖然夠,但沒有時時歸納總結,導致資訊沒有凝聚成知識或知識沒有串連。
這裡補充下 DP deep learning 的背景知識,暫且略過 DP 的定義,不影響閱讀。
所謂DP deep learning 從演算法的角度來說其實就是多做兩個額外的步驟:per-sample gradient clipping 和Gaussian noise addition;換句話說,只要你把gradient 依照這兩步驟處理完了(處理後的gradient 叫做private gradient),之後該怎麼用優化器就怎麼用,SGD/Adam 都可以。
至於最後演算法到底多 private,就是另一個子領域的問題了,稱為 privacy accounting theory。此領域相對成熟且需要極強的理論功底,由於本文專注於 optimization,按下不表。
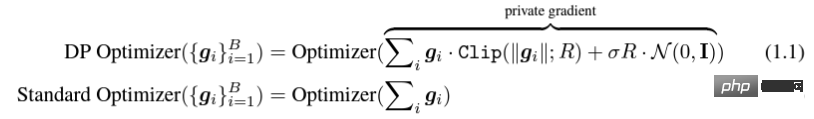
g_i 是 一個資料點的梯度(per-sample gradient),R 是 clipping threshold, sigma 是 noise multiplier。
其中 Clip 叫做 clipping function,就跟常規的 gradient clipping 一樣,梯度長於 R 就剪到 R,小於 R 就不動。
例如DP 版本的SGD 就是目前所有paper 都用的是隱私深度學習開山之作(Abadi, Martin, et al. "Deep learning with differential privacy.")中的clipping function,也稱為Abadi's clipping:圖片。
但這是完全不必要的,遵循第一原理,從 privacy accounting theory 出發,其實 clipping function 只需要滿足 Clip(g_i)*g_i 的模小於等於 R 就可以了。也就是說,Abadi's clipping 只是一種滿足這個條件的函數,但絕非唯一。
二、切入點
一篇文章的閃光點很多,但是並非都能為我所用,要結合自身的需求和擅長去判斷最大的貢獻是什麼。
這篇文章前兩個貢獻其實非常 empirical,也很難深入挖掘。而最後一個貢獻很有意思我仔細看了看超參數的ablation study 發現一個原作者沒有發現的點:在clipping threshold 足夠小的時候,其實clipping threshold(也就是clipping norm C,在上面的公式中和R是一個變數)沒有作用。
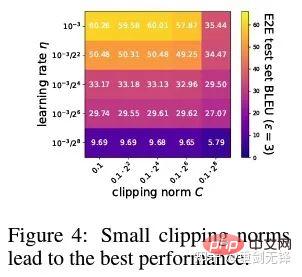
縱向來看 C=0.1,0.4,1.6 對 DP-Adam 沒什麼差別 [Xuechen et al. 2021]。
這引起了我的興趣,感覺背後一定有什麼原理。於是我手寫了他們所用的 DP-Adam 來看看為什麼,其實這很簡單:

如果 R 夠小,clipping 其實等價於 normalization!簡單代入private gradient(1.1),可以將R 從clipping 的部分和noising 的部分分別提出來:
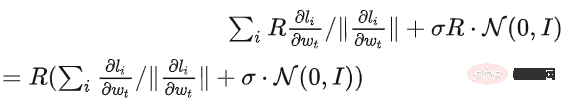
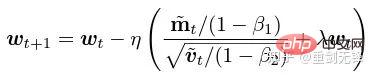

對 DP-SGD 且 R 夠小的時候,增大 10 倍 lr 等於增大 10 倍 R [https://arxiv.org/abs/2201.12328]。
當時我看到這篇文章的時候很興奮,因為又是一個證明 small clipping threshold 效果好的論文。
在科學界,連續的巧合背後往往有著隱藏的規律。
簡單地代換一下,發現SGD 比Adam 還好分析,(1.3)可以近似為:
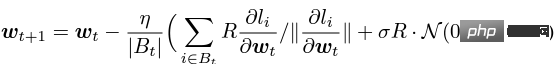
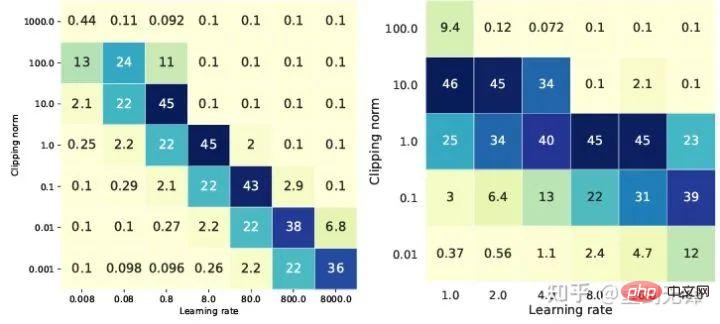
顯然R 又可以提出來,和學習率組合在一起,從理論上證明了Google 的觀察。
「Specifically, when the clipping norm is decreased k times, the learning rate should be increased k times to maintain similar accuracy.」
很可惜Google 只看到現象,沒有上升到理論的高度。這裡也有一個巧合,那就是上圖他們同時畫了兩種尺度的ablation study,只有左邊的尺度能看出對角線,光看右邊是沒有結論的......
#由於沒有自適應步長,SGD 不像Adam 一樣無視R,而是把R 看作學習率的一部分,所以也不需要單獨調節,反正學習率要調參就一起調了。
再將 SGD 的理論擴充到 momentum,所有 Pytorch 支援的最佳化器全都分析完畢。
五、從直覺到嚴謹
一個創新點是有了,但是Abadi's clipping 嚴格來說只是近似normalization,不能劃等號,也就沒法確鑿地分析收斂性。
根據多啦A 夢鐵人兵團原理,我直接命名normalization 為新的per-sample gradient clipping function,替代了整個領域用了6 年的Abadi clipping,這是我的第二個創新點。
經過剛才的證明,新的 clipping 嚴格不需要 R,所以稱為 automatic clipping (AUTO-V; V for vanilla)。
既然形式上與 Abadi's clipping 有不同,那麼 accuracy 就會有差異,而我的 clipping 可能有劣勢。
所以我需要寫程式碼測試我的新方法,而這只需要改動一行程式碼 (畢竟只是把圖片)。
事實上DP per-sample gradient clipping 這個方向主要就三種clipping functions, 除了Abadi's clipping 以外的兩種都是我提出的,一個是global clipping,還有一個就是這篇automatic clipping。而在先前的工作中,我就已經知道怎麼在各個流行的庫中改 clipping 了,我將修改方法放在文章最後一個 appendix。
經過我的測試,我發現史丹佛的文章中 GPT2 在整個訓練過程中,所有 itertation 和所有 per-sample gradient 都是 clip 過的。也就是說,至少在這一個實驗上,Abadi's clipping 完全等價於 automatic clipping。雖然後來的實驗的確有輸於 SOTA 的情況, 但這已經說明了我的新方法有足夠的價值:一個不需要調整 clipping threshold 的 clipping function,而且有時 accuracy 也不會犧牲。
六、 迴歸抽象思考
史丹佛的文章有兩大類語言模型的實驗,一類是GPT2 為模型的生成型任務,另一類是RoBERTa 為模型的分類型任務。雖然在生成任務上 automatic clipping 和 Abadi's clipping 等價,但是分類型任務卻總是差幾個點的準確率。
出於我自己的學術習慣,這時候我不會去換資料集然後專門挑我們佔優的實驗發表,更不會增加trick(例如做資料增強和魔改模型之類的)。我希望在完全公平的比較中, 只比較 per-sample gradient clipping 的前提下,盡可能做出最好的不含水分的效果。
事實上,在和合作者討論中我們發現:純粹的normalization 和Abadi's clipping 比梯度大小的資訊是完全拋棄的,也就是說對於automatic clipping,無論原始的梯度多大, clip 後都是R 這麼大,而Abadi 對於比R 小的梯度是保留了大小的資訊的。
基於這個想法,我們做了一個微小但極其巧妙的改動,稱為AUTO-S clipping (S 代表stable)
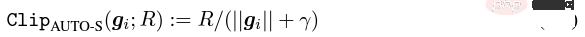
將R 和學習率融合後變成
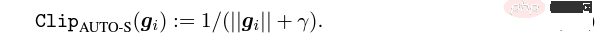
簡單一畫可以發現這個小小的 (一般設為0.01,其實設為別的正數都行,很穩健)就能保留梯度大小的資訊:
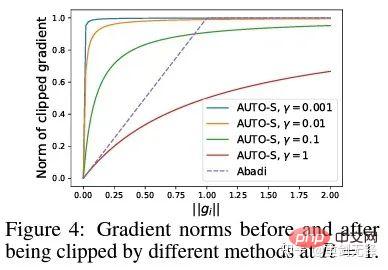
基於這個演算法,還是只改動一行,把史丹佛的程式碼重跑一遍,六個 NLP 資料集的 SOTA 就到手了。
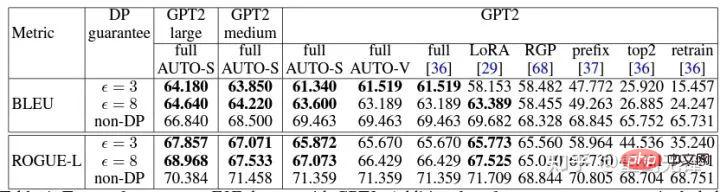
在 E2E 產生任務上,AUTO-S 超越了所有其他 clipping function,在 SST2/MNLI/QNLI/QQP 分類任務上也是如此。
七、要做通用演算法
史丹佛文章的一個限制是只專注於NLP,又很巧合的是:緊接著Google 刷了ImageNet 的DP SOTA 兩個月後,Google 子公司DeepMind 放出了一篇DP 在CV 大放異彩的文章,直接將ImageNet 準確率從48% 提升到84%!

論文網址:https://arxiv.org/abs/2204.13650
在這篇文章中,我第一時間去看優化器和clipping threshold 的選擇,直到我在附錄翻到這張圖:

DP-SGD 在ImageNet 上的SOTA 也是需要clipping threshold 夠小。
還是 small clipping threshold 效果最好!有了三篇高品質的文章支撐 automatic clipping,已經有了很強的動機了,我越發肯定自己的工作會是非常傑出的。
巧合的是DeepMind 這篇文章也是純實驗沒有理論,這也導致他們差點就領悟出了他們可以從理論上不需要R,事實上他們真的非常接近我的想法了,他們甚至已經發現了R 是可以提取出來和學習率融合的(有興趣的同學可以看看他們的公式(2)和(3))。但 Abadi's clipping 的慣性太大了... 即使他們總結出了規律卻沒有更進一步。

DeepMind 也發現了 small clipping threshold 效果最好,但沒有理解為什麼。
受這篇新工作的啟發,我開始著手做CV 的實驗,讓我的演算法能被所有DP 研究者使用,而不是NLP 搞一套方法,CV 搞另一套。
好的演算法就是應該通用好用,事實也證明 automatic clipping 在 CV 資料集上同樣能取得 SOTA。
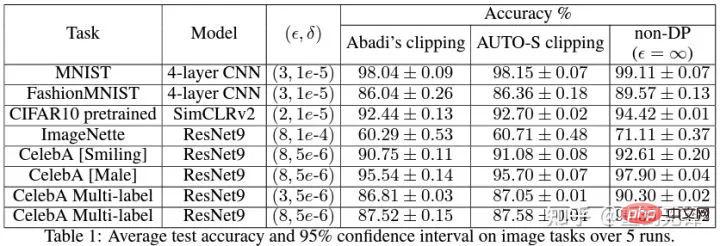
八、理論為骨實驗為翼
#縱觀以上所有的論文,都是SOTA 提升顯著、工程效果拔滿,但是理論完全空白。
當我做完所有實驗的時候,這份工作的貢獻已經超過了一篇頂會的要求:我將經驗上small clipping threshold 所產生的DP-SGD 和DP-Adam的參數影響大大簡化;提出了新的clipping function 而不犧牲運算效率、隱私性,還不用調參;小小的γ 修復了Abadi's clipping 和normalization 對梯度大小資訊的破壞;充足的NLP 和CV 實驗都取得了SOTA 的準確率。
我還沒滿意。一個沒有理論支撐的優化器,還是無法為深度學習做出實質貢獻。每年頂會提出的新優化器有幾十個,第二年全都掃進故紙堆。 Pytorch 官方支援的、業界真正在用的,還是那麼幾個。
為此我和合作者們額外花了兩個月做了 automatic DP-SGD 收斂性分析,過程艱難但最後的證明簡化到極致。結論也很簡單:將 batch size、learning rate、model size、sample size 等變數對收斂的影響都定量地表達出來,並且符合所有已知的 DP 訓練行為。
特別的,我們證明了 DP-SGD 雖然收斂的比標準的 SGD 慢,但是 iteration 趨於無窮的話,收斂的速度都是一個數量級的。這為隱私運算提供了信心:DP 模型收斂,雖遲但到。
九、撞車了...
終於,寫了 7 個月的文章完稿了,沒想到巧合還沒停。 5 月NeurIPS 投稿,6 月14 日內部修改完放arXiv,結果6 月27 日看到微軟亞研究院(MSRA)發表了一篇和我們撞車的文章,提出的clipping 和我們的automatic clipping 一模一樣:

和我們的 AUTO-S 分毫不差。
#仔細看了看,連收斂性的證明都差不多。而我們兩組人又沒有交集,可以說隔著太平洋的巧合誕生了。
這裡稍微講一下兩篇文章的不同:對方文章更偏理論,例如額外分析了Abadi DP-SGD 的收斂(我只證了automatic clipping,也就是他們文中的DP- NSGD,可能我也不知道咋整DP-SGD);用的假設也有一些不同;而我們實驗做的多一些大一些(十幾個數據集),更顯式地建立了Abadi's clipping 和normalization 的等價關係,如Theorem 1 和2 解釋為什麼R 可以不用調參。
既然是同時期的工作,我很開心能有人不謀而合,互相能補充共同推動這個演算法,讓整個社群盡快相信這個結果並從中受益。當然,私心來說,也提醒自己下一篇要加速了!
#十、總結
回顧這篇文章的創作歷程,從起點來看,基本功一定是前提,而另一個重要的前提是自己心中一直念念不忘調參這個痛點問題。正是久旱,所以讀到合適的文章才能逢甘露。至於過程,核心在於將觀察數學化理論化的習慣,在這個工作中代碼實現能力反倒不是最重要的。我會再寫一篇專欄著重講講另一個硬派程式碼工作;最後的收斂分析,也是靠合作者和自己的不將就。所幸好飯不怕晚,繼續前進!
作者簡介
卜至祺,劍橋大學本科畢業,賓州大學博士,現任亞馬遜AWS AI 資深研究科學家,其研究方向為差分隱私與深度學習,專注優化演算法和大規模計算。
以上是我是如何從頭開始寫一篇頂尖論文的的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 Stable Diffusion 3論文終於發布,架構細節大揭秘,對復現Sora有幫助?
Mar 06, 2024 pm 05:34 PM
Stable Diffusion 3論文終於發布,架構細節大揭秘,對復現Sora有幫助?
Mar 06, 2024 pm 05:34 PM
StableDiffusion3的论文终于来了!这个模型于两周前发布,采用了与Sora相同的DiT(DiffusionTransformer)架构,一经发布就引起了不小的轰动。与之前版本相比,StableDiffusion3生成的图质量有了显著提升,现在支持多主题提示,并且文字书写效果也得到了改善,不再出现乱码情况。StabilityAI指出,StableDiffusion3是一个系列模型,其参数量从800M到8B不等。这一参数范围意味着该模型可以在许多便携设备上直接运行,从而显著降低了使用AI
 你是否真正掌握了座標系轉換?自動駕駛離不開的多感測器問題
Oct 12, 2023 am 11:21 AM
你是否真正掌握了座標系轉換?自動駕駛離不開的多感測器問題
Oct 12, 2023 am 11:21 AM
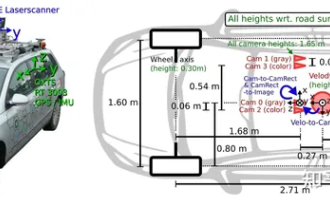
一先導與重點文章主要介紹自動駕駛技術中幾種常用的座標系統,以及他們之間如何完成關聯與轉換,最終建構出統一的環境模型。這裡重點理解自車到相機剛體轉換(外參),相機到影像轉換(內參),影像到像素有單位轉換。 3d向2d轉換會有對應的畸變,平移等。重點:自車座標系相機機體座標系需要被重寫的是:平面座標系像素座標系難點:要考慮影像畸變,去畸變和加畸變都是在像平面上去補償二簡介視覺系統一共有四個座標系:像素平面座標系(u,v)、影像座標系(x,y)、相機座標系()與世界座標系()。每種座標系之間均有聯繫,
 自動駕駛與軌跡預測看這篇就夠了!
Feb 28, 2024 pm 07:20 PM
自動駕駛與軌跡預測看這篇就夠了!
Feb 28, 2024 pm 07:20 PM
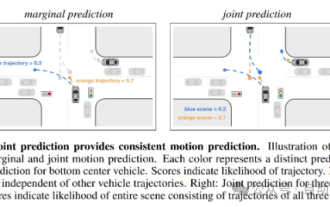
軌跡預測在自動駕駛中承擔著重要的角色,自動駕駛軌跡預測是指透過分析車輛行駛過程中的各種數據,預測車輛未來的行駛軌跡。作為自動駕駛的核心模組,軌跡預測的品質對於下游的規劃控制至關重要。軌跡預測任務技術堆疊豐富,需熟悉自動駕駛動/靜態感知、高精地圖、車道線、神經網路架構(CNN&GNN&Transformer)技能等,入門難度很高!許多粉絲期望能夠盡快上手軌跡預測,少踩坑,今天就為大家盤點下軌跡預測常見的一些問題和入門學習方法!入門相關知識1.預習的論文有沒有切入順序? A:先看survey,p
 DualBEV:大幅超越BEVFormer、BEVDet4D,開卷!
Mar 21, 2024 pm 05:21 PM
DualBEV:大幅超越BEVFormer、BEVDet4D,開卷!
Mar 21, 2024 pm 05:21 PM
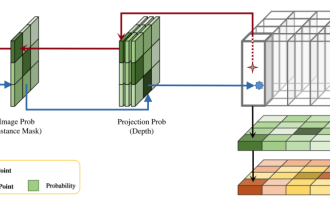
這篇論文探討了在自動駕駛中,從不同視角(如透視圖和鳥瞰圖)準確檢測物體的問題,特別是如何有效地從透視圖(PV)到鳥瞰圖(BEV)空間轉換特徵,這一轉換是透過視覺轉換(VT)模組實施的。現有的方法大致分為兩種策略:2D到3D和3D到2D轉換。 2D到3D的方法透過預測深度機率來提升密集的2D特徵,但深度預測的固有不確定性,尤其是在遠處區域,可能會引入不準確性。而3D到2D的方法通常使用3D查詢來採樣2D特徵,並透過Transformer學習3D和2D特徵之間對應關係的注意力權重,這增加了計算和部署的
 首個多視角自動駕駛場景影片產生世界模型 | DrivingDiffusion: BEV資料與模擬新思路
Oct 23, 2023 am 11:13 AM
首個多視角自動駕駛場景影片產生世界模型 | DrivingDiffusion: BEV資料與模擬新思路
Oct 23, 2023 am 11:13 AM
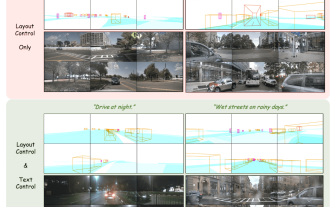
作者的一些個人思考在自動駕駛領域,隨著BEV-based子任務/端到端方案的發展,高品質的多視圖訓練資料和相應的模擬場景建立愈發重要。針對當下任務的痛點,「高品質」可以解耦成三個面向:不同維度上的長尾場景:如障礙物資料中近距離的車輛以及切車過程中精準的朝向角,以及車道線資料中不同曲率的彎道或較難收集的匝道/匯入/合流等場景。這些往往靠大量的資料收集和複雜的資料探勘策略,成本高昂。 3D真值-影像的高度一致:當下的BEV資料取得往往受到感測器安裝/標定,高精地圖以及重建演算法本身的誤差影響。這導致了我
 GSLAM | 一個通用的SLAM架構和基準
Oct 20, 2023 am 11:37 AM
GSLAM | 一個通用的SLAM架構和基準
Oct 20, 2023 am 11:37 AM
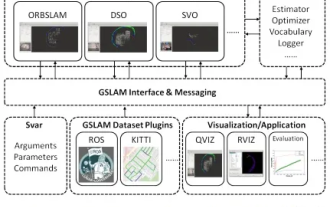
突然發現了一篇19年的論文GSLAM:AGeneralSLAMFrameworkandBenchmark開源程式碼:https://github.com/zdzhaoyong/GSLAM直接上全文,感受這項工作的品質吧~1摘要SLAM技術最近取得了許多成功,並吸引了高科技公司的關注。然而,如何同一現有或新興演算法的介面,一級有效地進行關於速度、穩健性和可移植性的基準測試仍然是問題。本文,提出了一個名為GSLAM的新型SLAM平台,它不僅提供評估功能,還為研究人員提供了快速開發自己的SLAM系統的有用
 NeRF與自動駕駛的前世今生,近10篇論文總結!
Nov 14, 2023 pm 03:09 PM
NeRF與自動駕駛的前世今生,近10篇論文總結!
Nov 14, 2023 pm 03:09 PM
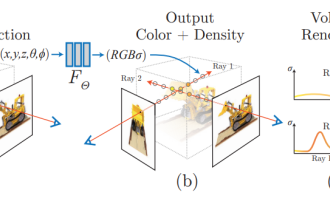
神經輻射場(NeuralRadianceFields)自2020年被提出以來,相關論文數量呈指數增長,不僅成為了三維重建的重要分支方向,也逐漸作為自動駕駛重要工具活躍在研究前沿。 NeRF這兩年異軍突起,主要因為它跳過了傳統CV重建pipeline的特徵點提取和匹配、對極幾何與三角化、PnP加BundleAdjustment等步驟,甚至跳過mesh的重建、貼圖和光追,直接從2D輸入影像學習一個輻射場,然後從輻射場輸出逼近真實照片的渲染影像。也就是說,讓一個基於神經網路的隱式三維模型,去擬合指定視角
 華人團隊斬獲最佳論文、最佳系統論文獎項,CoRL研究成果獲獎公佈
Nov 10, 2023 pm 02:21 PM
華人團隊斬獲最佳論文、最佳系統論文獎項,CoRL研究成果獲獎公佈
Nov 10, 2023 pm 02:21 PM
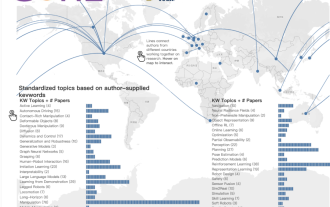
自2017年首次舉辦以來,CoRL已成為了機器人學與機器學習交叉領域的全球頂級學術會議之一。 CoRL是機器人學習研究的單一主題會議,涵蓋了機器人學、機器學習和控制等多個主題,包括理論與應用2023年的CoRL大會將於11月6日至9日在美國亞特蘭大舉行。根據官方數據透露,今年有來自25個國家的199篇論文入選CoRL。熱門主題包括操作、強化學習等。雖然相較於AAAI、CVPR等大型AI學術會議,CoRL的規模較小,但隨著今年大模型、具身智能、人形機器人等概念的熱度上升,值得關注的相關研究也會






