「在一個帶權有向圖G=(V,E)中,每條邊的權是一個實數。另外,還給定V中的一個頂點,稱為源。
計算從來源到其他所有各頂點的最短路徑長度,這就是單源最短路徑(SSSP)問題。」
半個多世紀以來,世界各地的研究人員一直在努力解決這個問題。而現在,這個演算法謎題終於被哥本哈根大學計算機科學系的研究團隊成功解決。
負權值SSSP演算法:速度快、效率高

論文連結:https:/ /arxiv.org/abs/2203.03456
接受採訪時,研究人員Christian Wulff-Nilsen稱,他們的解決方案是第一個突破存在30多年的Õ(n(4/3) log W)運算時間約束的,負權值的SSSP組合演算法。
關於SSSP有兩個經典演算法:Dijkstra演算法(迪克斯特拉演算法)和Bellman-Ford演算法(貝爾曼-福特演算法),兩者都有各自的限制。
Dijkstra演算法運算時間最短,能達到近線性時間 O(m #n log n) ,但不能計算負權值邊。
Bellman-Ford演算法可以計算負權值邊,但運算時間過長,達到O(mn)。目前,最頂尖的解決負權邊的SSSP演算法都依賴複雜的連續最佳化和動態代數和圖形演算法。這就導致即使後世學者不斷優化該演算法,其運算時間仍需Õ(n(4/3) log W)。這個運算時間的約束已經存在三十年之久。
面對這些限制,Wulff-Nilsen提出了兩個問題:
1)帶負權邊演算法的運算能否達到近線性時間?
2)能否用簡單的工具來達到這個目的?
有沒有一種方法,可以既要時間,又要品質呢?
別說,還真有。
Wulff-Nilsen提出的演算法為影像縮放演算法,被簡易影像分解演算法Low Diameter Decomposition強化。通常情況,此分解演算法只用於非負權邊的圖形分解,而該研究的貢獻之一就在於將其運用到負權邊影像中,加強負權邊SSSP遞歸縮放演算法。
推導過程
Wulff-Nilsen以Johnson的價格演算法為基礎。提出:在圖像G = (V, E, w)中,令Φ為任意函數:V→ Z。令w(Φ)為權函數:
定義:,則:##。 在圖片G = (V, E,w)和圖片#G' ##在 #= (V, E,w')中,若:1)影像G中的最短距離與影像G'中的最短距離相等,反之亦然;2)G只在##G'含有負權環時含有負權環,則影像G與影像G'##相等。 推論2.7考慮到任意圖像
與價格函數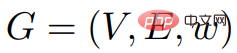 Φ。在 u, v ∈ V 中,。
Φ。在 u, v ∈ V 中,。
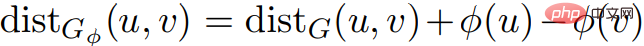 C中,。
C中,。
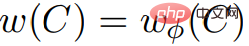 G和相等。如果
G和相等。如果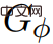 ,,
,,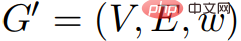 那麼
那麼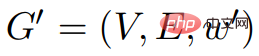
 #G和#G'相等。
#G和#G'相等。
該演算法的目的是在計算價格函數#Φ時,在GΦ中的所有邊權都為非負,假設不存在負權環。之後就可以在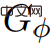 上執行Dijkstra演算法。
上執行Dijkstra演算法。
之後,Wulff-Nilsen開始介紹自己的演算法框架。
首先,Wulff-Nilsen假設存在一個演算法Dijkstra(G,s),輸入無負權邊的圖形G,頂點s ∈ V,G中的s輸出最短路徑樹。運轉時間為O(m n log n)。 # 如果G是DAG(有向無環圖),計算一個價格函數Φ,使 單源最短路徑問題的目的是找到從給定起始節點到網路中所有其他節點的最短路徑。 網路表示為由節點和它們之間的連接組成的圖形,稱為邊。 每條邊都有一個方向(例如,這可用於表示單向道路)以及一個權重,用於表示沿著該邊行駛的成本。如果所有邊權重都是非負的,則可以使用經典的Dijkstra演算法在幾乎線性的時間內解決問題。 新結果在與Dijkstra演算法幾乎相同的時間內解決了這個問題,但也允許負邊權重。在 之後,Wulff-Nilsen提到了組合工具中最重要的兩個演算法:ScaleDown和SPmain# 。 ScaleDown演算法分階段運行,在最後一個階段它用ElimNeg( 這意味著,對於所有 如果演算法終止,則對於所有 這表示對所有, 透過歸納法,假設理論適用於, 因此,透過 由於 因此得出結論:如果 由此可以證明,SPmain演算法的正確性。 至此,Wulff-Nilsen的負權值SSSP解決方案中最重要的兩個演算法都證明成立。新演算法在保證近線性時間的同時,成功引入了負權值。 去年,Wulff -Nilsen在同一領域取得了另一項突破,結果涉及如何在隨時間變化的網路中找到最短路徑。他對最近謎語的解決方案建立在這項工作的基礎上。 他認為,解決SSSP問題可以為演算法鋪平道路,不僅可以幫助電動車立即計算到達目的地的最快路線,而且能保證以最節能的方式做到這一點。 Wulff-Nilsen解釋:「我們的演算法裡加入了負權這個以前演算法沒有的維度。一個實際的例子是在山間駕駛時,有了負權這一維度,導航系統可以為電動車車主推薦下坡路多的路線,使電動車可以在下坡時進行充電。」 #Wulff-Nilsen也表示,他們的演算法不僅可以用於電動路線規劃,還能用來監控金融業的投機行為。他說:「原則上,演算法可以用來為中央銀行等用戶預警,警告投機者在投機買賣各種貨幣。現在,許多不法之徒利用電腦犯罪,但由於我們的演算法如此之快,或許能夠被用來監測,在人們利用漏洞之前及時發現。」 1959年,當Dijkstra首次提出最短距離問題時,可能他也不會想到,60多年來,一直有人不斷優化這個問題的方案。或許也會驚訝,謎題的答案竟然有如此豐富的內涵。 或許,這就是科學的魅力。 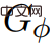 具有非負權邊是很簡單的:只需在拓樸的v1, ..., vn上循環,並設定Φ(vi),使所有進入的邊權值為非負值。
具有非負權邊是很簡單的:只需在拓樸的v1, ..., vn上循環,並設定Φ(vi),使所有進入的邊權值為非負值。 
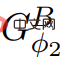 )來計算價格函數Φ2。如果ElimNeg終止,它將傳回價格函數ψ′,#讓
)來計算價格函數Φ2。如果ElimNeg終止,它將傳回價格函數ψ′,#讓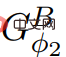 所有邊值非負;換句話說,因為
所有邊值非負;換句話說,因為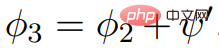 ,所以
,所以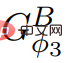 中不包含負權值。
中不包含負權值。 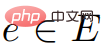 ,
,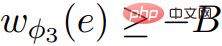 都滿足條件(因為
都滿足條件(因為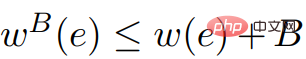 )。由此證明了 ScaleDown輸出的正確性。
)。由此證明了 ScaleDown輸出的正確性。 
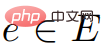 和
和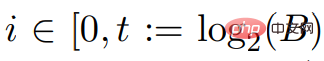 ,
,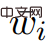 ##是積分,並且對於所有 #,
##是積分,並且對於所有 #,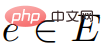 。
。 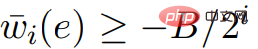
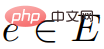 。
。 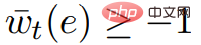 因此圖形G*具有非負權值。
因此圖形G*具有非負權值。 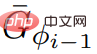 演算法第5行對ScaleDown
演算法第5行對ScaleDown 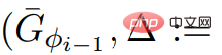
 的呼叫滿足必要的輸入屬性。
的呼叫滿足必要的輸入屬性。 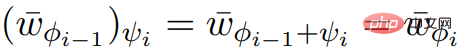 #和ScaleDown的Output,可以得到。
#和ScaleDown的Output,可以得到。 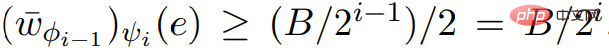
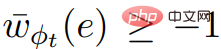 ,若令C為
,若令C為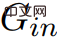 中任意負權環,由於
中任意負權環,由於 中的所有權值都為2n的倍數,且
中的所有權值都為2n的倍數,且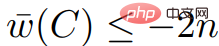 ;又知
;又知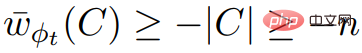 ,故
,故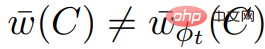 與推論2.7不符。
與推論2.7不符。 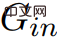 #包含負權環,則演算法不會終止。
#包含負權環,則演算法不會終止。 #60年後,尋求答案不僅為了解謎
以上是60年前謎題!哥本哈根大學研究人員解決「單源最短路徑」問題的詳細內容。更多資訊請關注PHP中文網其他相關文章!




