要說 AI 領域今年影響力最大的進展,爆火的 AI 作圖絕對是其中之一。設計者只需要輸入圖片的文字描述,就可以由 AI 產生一張極高品質的高解析度圖片。目前,使用範圍最廣的當屬 StabilityAI 的開源模型 Stable Diffusion,模型一經開源就在社區引起了廣泛的討論。
然而,擴散模型在使用上最大的問題就是其極慢的取樣速度。模型取樣需要從純雜訊圖片出發,一步一步不斷去噪,最終得到清晰的圖片。在這個過程中,模型必須串行地計算至少50 到100 步才可以獲得較高質量的圖片,這導致生成一張圖片需要的時間是其它深度生成模型的50 到100 倍,極大地限制了模型的部署和落地。
為了加速擴散模型的取樣,許多研究者從硬體最佳化的角度出發,例如Google 使用JAX 語言將模型編譯運行在TPU 上,OneFlow 團隊[1] 使用自研編譯器將Stable Diffusion 做到了「一秒出圖」。這些方法都基於 50 步的取樣演算法 PNDM[2],該演算法在步數減少時取樣效果會急劇下降。
就在幾天前,這項紀錄又被刷新了! Stable Diffusion 的官方 Demo[3]更新顯示,採樣 8 張圖片的時間從原來的 8 秒鐘直接被縮短至了 4 秒鐘!快了整整一倍!
而基於自研深度學習編譯器技術的OneFlow 團隊更是在不降低採樣效果的前提下,成功將之前的「一秒出圖」 縮短到了「半秒出圖」!在 GPU 上僅使用不到 0.5 秒就可以獲得一張高清的圖片!相關工作已發佈在[1] 中。
事實上,這些工作的核心驅動力都來自於清華大學朱軍教授帶領的TSAIL 團隊所提出的DPM-Solver,一種針對擴散模型特殊設計的高效求解器:此演算法無需任何額外訓練,同時適用於離散時間與連續時間的擴散模型,可以在20 到25 步內幾乎收斂,並且只用10 到15 步也能獲得非常高品質的採樣。在 Stable Diffusion 上,25 步的 DPM-Solver 可以獲得優於 50 步 PNDM 的採樣質量,因此採樣速度直接翻倍!
專案連結:
擴散模型透過定義一個不斷加雜訊的前向過程來將圖片逐步變為高斯噪聲,再定義了一個逆向過程將高斯噪聲逐步去噪變為清晰圖片以得到採樣:

##在採樣過程中,根據是否添加額外的噪聲,可以將擴散模型分為兩類:一類是擴散隨機微分方程模型(Diffusion SDE),另一類是擴散常微分方程(Diffusion ODE)。兩個模型的訓練目標函數都一樣,透過最小化與雜訊的均方誤差來訓練一個「雜訊預測網路」:
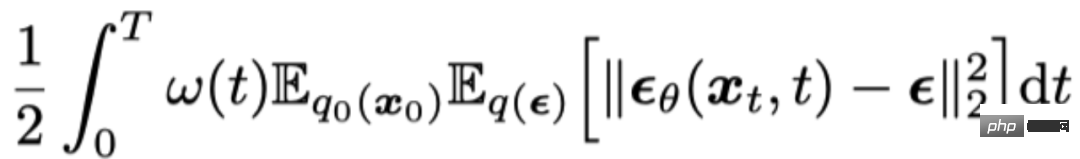
基於Diffusion SDE 的取樣過程可以視為離散化如下隨機微分方程:
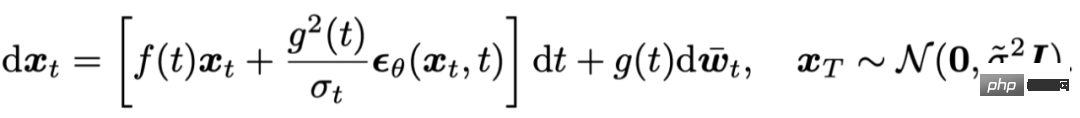
#並且[4] 中證明,DDPM[5] 是對上述SDE 的一階離散化。
而基於 Diffusion ODE 的取樣過程可以視為離散化如下常微分方程:#
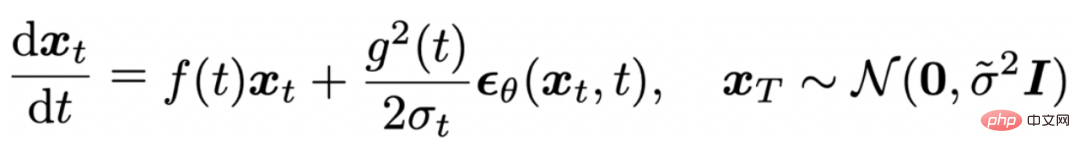
並且 [6] 中證明,DDIM[7]是對上述 ODE 的一階離散化。
然而,這些一階的離散化方法收斂速度極慢,擴散模型的取樣通常需要 100 到 1000 次串列計算才可以得到高品質的圖片。通常情況下,為了加速擴散模型的取樣,研究者往往透過對Diffusion ODE 使用高階求解器來加速,例如經典的Runge-Kutta 方法(RK45),這是因為ODE 不會帶來額外的隨機性,離散化步長可以相對選取得更大一些。在給定s 時刻的解後,Runge-Kutta 方法基於離散化如下積分:

#這樣的離散化將Diffusion ODE 整體看做一個黑盒,損失了ODE 的已知訊息,在小於50 步的情況下就難以收斂了。
DPM-Solver 基於Diffusion ODE 的半線性(semi-linear)結構,透過精確且解析地計算ODE 中的線性項,我們可以得到:

剩餘的積分項是一個關於時間的複雜的積分。然而,DPM-Solver 的提出者發現,該積分可以透過對log-SNR(對數訊號雜訊比)做換元後得到一個非常簡單的形式:
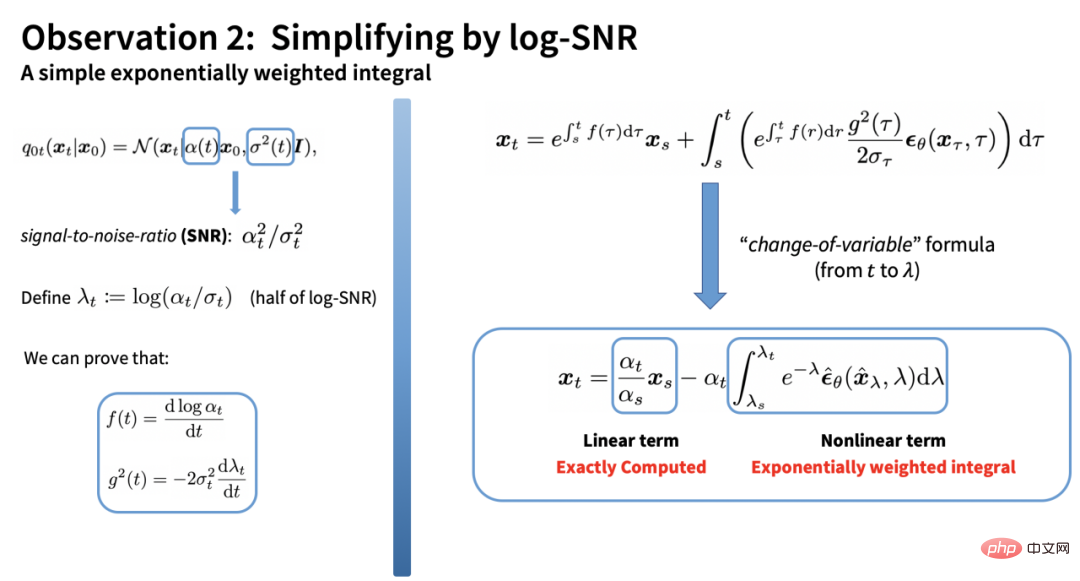
剩餘的積分是一個關於雜訊預測模型的指數積分(exponentially weighted integral)。透過對雜訊預測模型做泰勒展開,我們可以得到該積分的一個估計值:
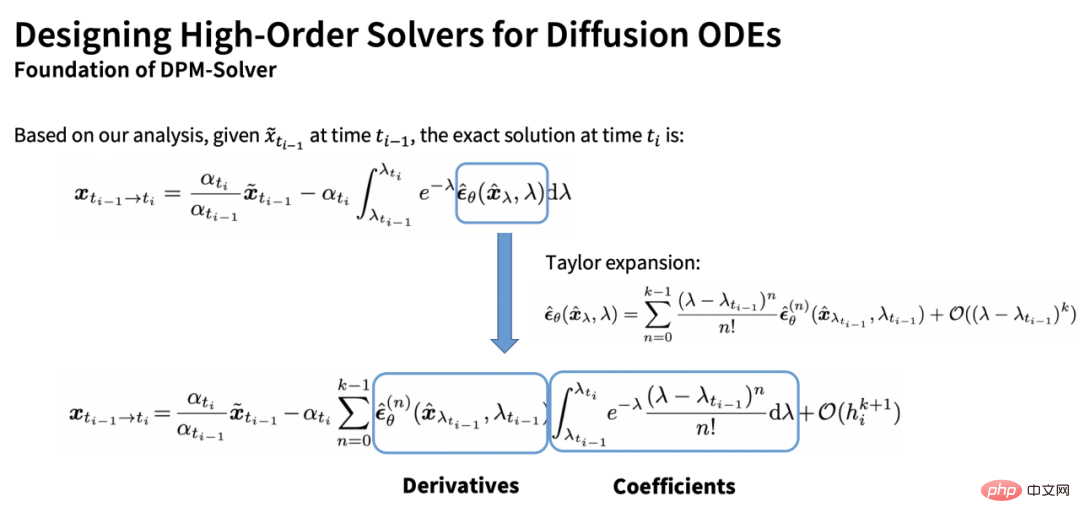
該估計值中存在兩項:一項是全導數部分(向量),另一項是係數部分(標量)。 DPM-Solver 的另一個核心貢獻是,該係數可以透過分部積分被解析地計算:
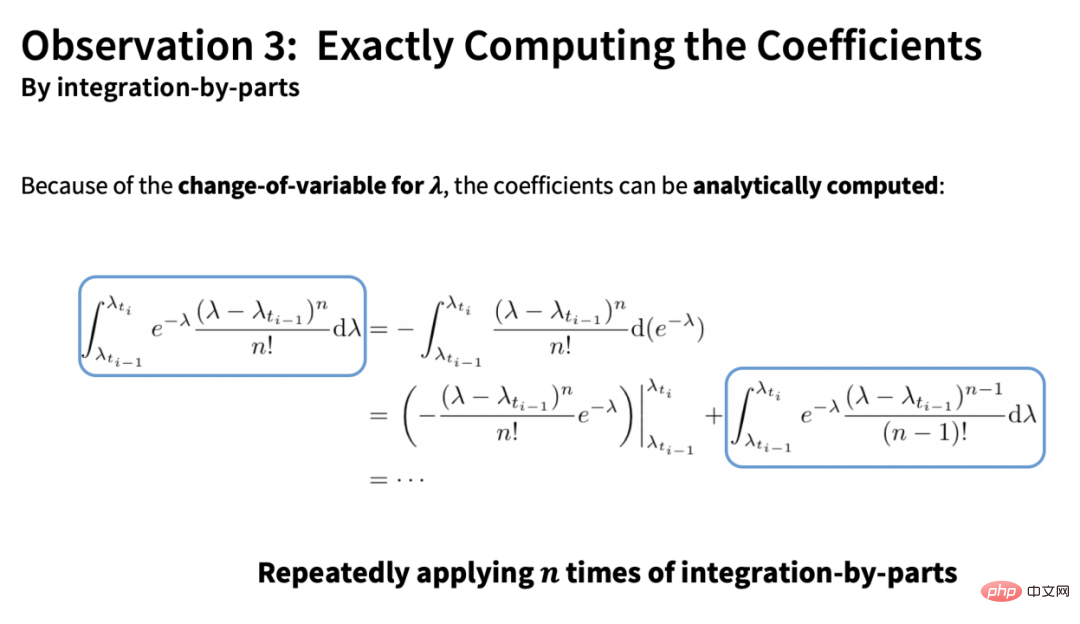
而剩餘的全導數部分則可以透過傳統ODE 求解器的數值方法來近似估計值(無需任何求導運算):

#基於以上4 點,DPM-Solver 做到了盡可能地準確計算所有已知項,只對神經網路部分做近似,因此最大程度地減小了離散化誤差:
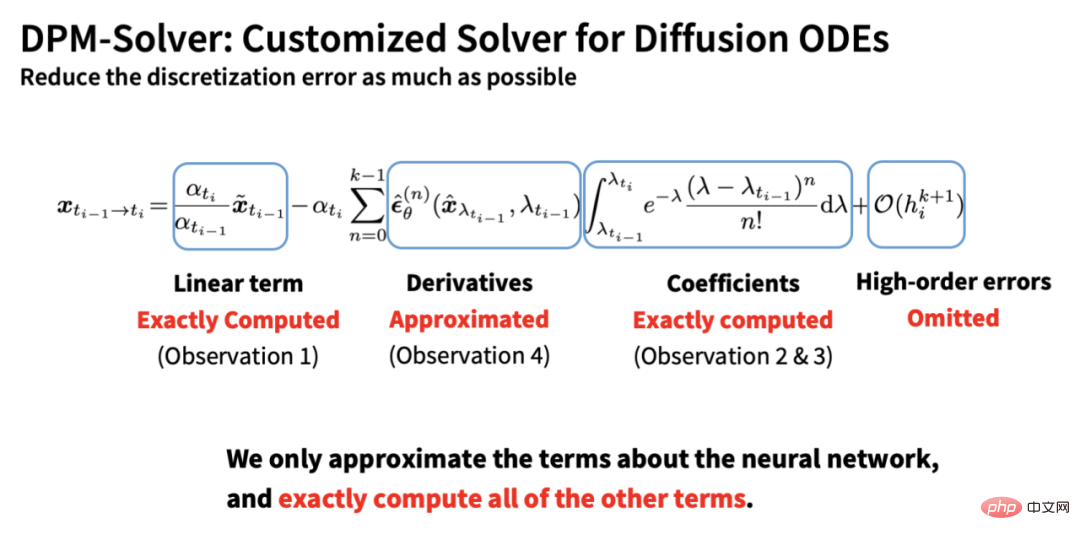
此外,基於此推導,我們可以得到DDIM 本質上是DPM-Solver 的一階形式,這也能解釋為什麼DDIM 在步數較少時依然可以獲得很好的加速效果:
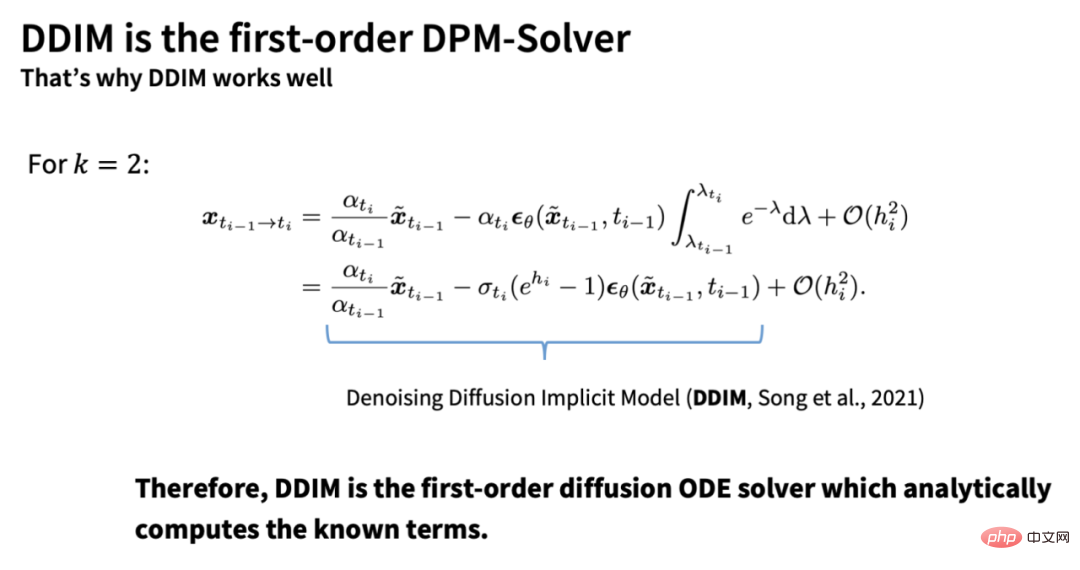
在實驗中,DPM-Solver 獲得了遠超其它採樣演算法的加速效果,僅在15-20 步就幾乎可以收斂:
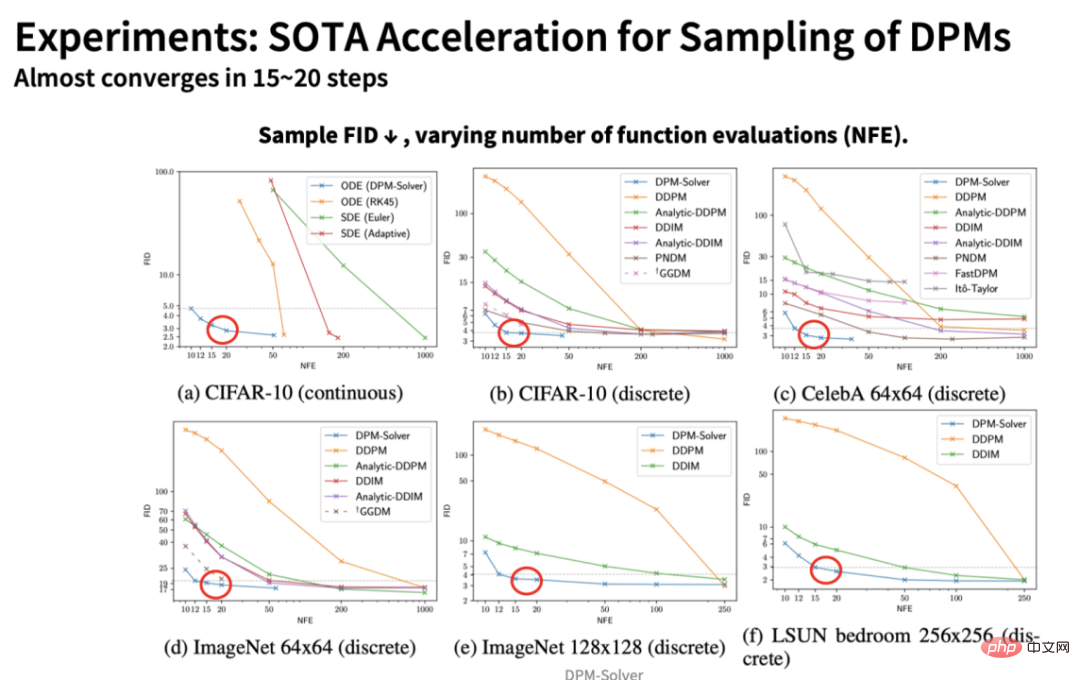
並且在論文中定量的結果顯示,DPM-Solver 引入的額外計算量完全可以忽略,即對於步數的加速效果直接正比於時間上的加速效果——因此,基於25 步的DPM-Solver,Stable-Diffusion 模型的採樣速度直接翻倍!例如,下圖展示了不同取樣演算法在Stable-Diffusion 上隨著步數變化的效果,可見DPM-Solver 在10 到15 步就可以獲得非常高品質的取樣:

DPM-Solver 的使用非常簡單,既可以基於作者提供的官方程式碼,也可以使用主流的Diffusers 函式庫。例如,基於作者提供的官方程式碼(https://github.com/LuChengTHU/dpm-solver),只需要3 行:

官方程式碼對4 種擴散模型都進行了支援:
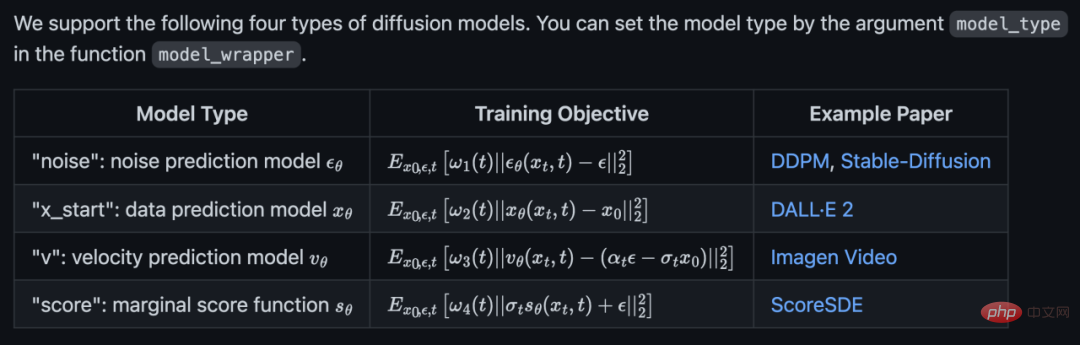
##並且同時支援unconditional sampling、classifier guidance 和classifier-free guidance:

而基於Diffusers 函式庫的DPM-Solver 同樣很簡單,只需要定義scheduler 即可:
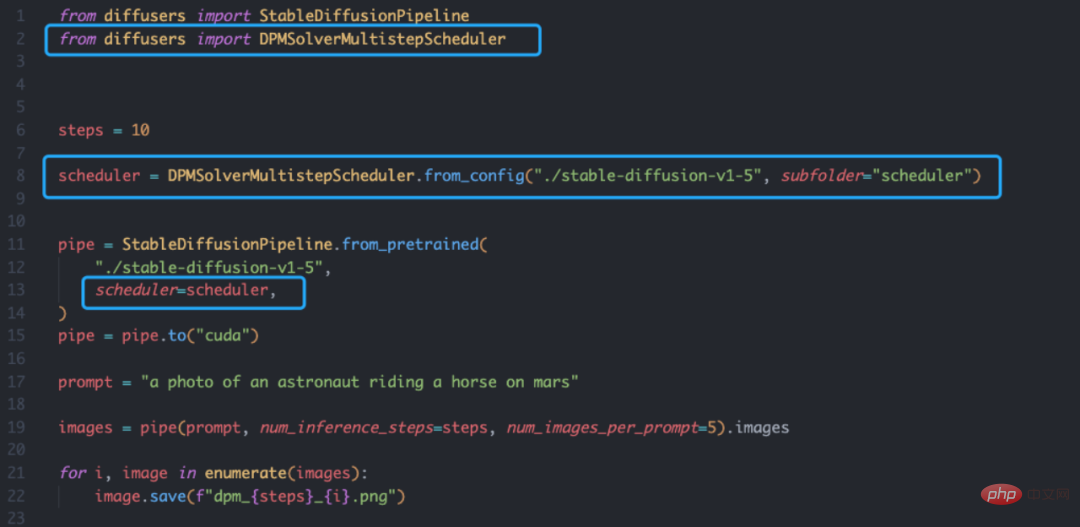
此外,作者團隊也提供了一個線上Demo:https://huggingface.co/spaces/LuChengTHU/dpmsolver_sdm
下圖是15 步的例子,可以看到影像品質已經非常高:
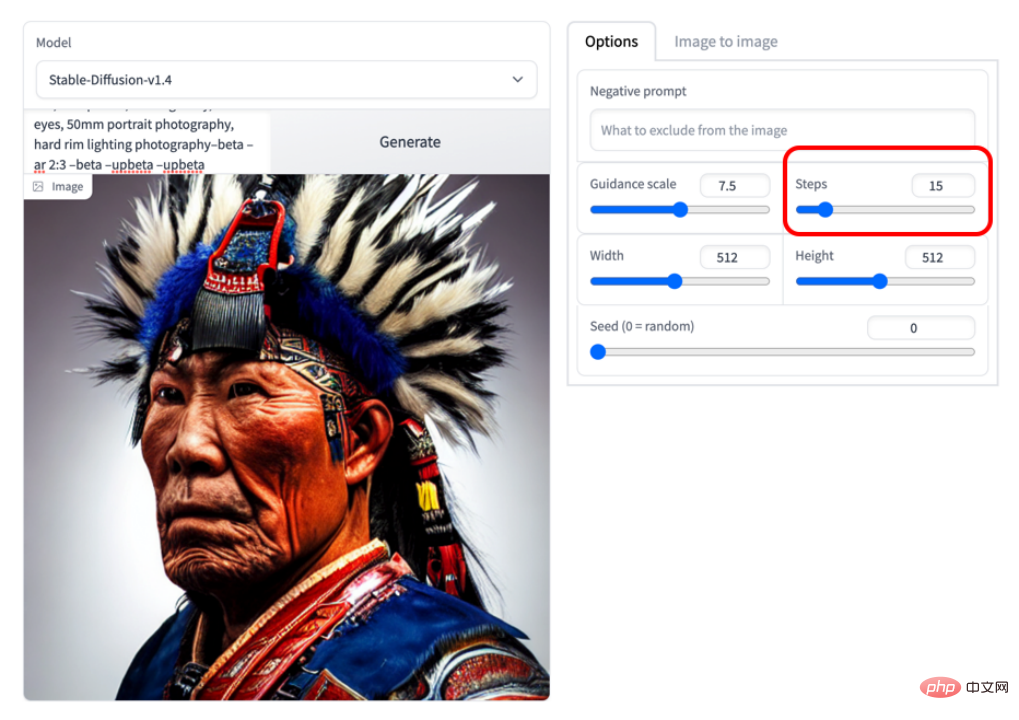
#相信基於DPM-Solver,擴散模型的取樣速度將不再是瓶頸。
關於作者DPM-Solver 論文一作是來自清華大學TSAIL 團隊的路橙博士,他在知乎上關於擴散模型的討論中也寫了一篇關於擴散模型原理的入門介紹,目前已有2000 讚:https://www.zhihu.com/question/536012286/answer/2533146567
清華大學TSAIL 團隊長期致力於貝葉斯機器學習的理論和演算法研究,是國際上最早研究深度機率生成模型的團隊之一,在貝葉斯模型、高效演算法和機率編程庫方面取得了系統深入的研究成果。團隊另一位博士生鮑凡提出Analytic-DPM [8][9],為擴散模型的最優均值和方差給出了簡單、令人吃驚的解析形式,獲得 ICLR 2022 Outstanding Paper Award。在機率編程方面,機器之心早在2017 年就報道了該團隊發布的“ZhuSuan” 深度機率編程庫(https://zhusuan.readthedocs.io/en/latest/)[10],是國際上最早的深度機率模型導向的程式庫之一。另外,值得一提的是,擴散機率模型的兩位核心作者宋颮和宋佳銘,本科時均在朱軍教授的指導下做科研訓練,後來都去了史丹佛大學讀博士。論文的合作者周聿浩、陳鍵飛、李崇軒,也是TSAIL組培養的優秀博士生,週聿浩為在讀,陳鍵飛和李崇軒,也是TSAIL組培養的優秀博士生,週聿浩為在讀,陳鍵飛和李崇軒分別在清華大學計算機系、人民大學高瓴人工智慧學院任教。
#
以上是Stable Diffusion採樣速度翻倍!僅需10到25步的擴散模型採樣演算法的詳細內容。更多資訊請關注PHP中文網其他相關文章!




