雜湊和雜湊都來自單字hash，前者是音譯，後者是意譯。是一種可以將任意長度的二進位值映射為固定長度二進位值的演算法，映射後固定長度的二進位值稱為雜湊值。一個優秀的雜湊演算法需要滿足以下幾點要求：
不能從雜湊值反向推導出原始資料；
對輸入資料非常敏感，一個bit不同就會導致哈希值非常不一樣；
散列衝突的機率要很小；
哈希演算法的計算過程要足夠簡單高效，即使原始資料很長，也能很快得到哈希值；
比較常見的雜湊加密演算法有MD5(MD5 Message-Digest Algorithm, MD5訊息摘要演算法)和SHA(Secure Hash Algorithm, 安全雜湊演算法)。
無法從雜湊值密文反推出明文密碼，且雜湊衝突機率比較小，這兩點確保了雜湊演算法作為安全加密手段的可靠性。
為什麼雜湊演算法不能完全避免雜湊衝突，只能盡量減少？
鴿巢原理告訴我們，11個鴿子飛進10個鴿子籠，那麼必定有一個鴿子籠裡面有2隻及以上的鴿子。那麼散列值是固定長度的，也就決定了散列值可以被窮舉，但是理論上原始資料是無窮無盡的，因此必定有可能會導致散列衝突。
這種應用場景用到了雜湊演算法的特性1和3，其中3保證了密碼被正向破解的難度很大（以MD5為例，雜湊值長度為128位，有2 ^128個不同的雜湊值，很難被破解）。
安全領域沒有絕對的安全，雖然MD5很難被破解，但是還是有辦法被破解的，例如使用彩虹表匹配可以很輕鬆地破解常見密碼。
所以一般我們會使用加鹽的雜湊演算法來進行安全加密，而加鹽的方法需要嚴格保密，如此讓破解的難度和成本都大大增加。
我們在校驗兩個檔案是否一樣的時候，是不能簡單地透過檔案名稱來進行判斷的。因為同名檔案的存在太常見了。
我們可以從大檔案中按照特定的規則取一些二進位數據，利用哈希演算法得出哈希值作為該檔案的唯一標誌。如此相同的檔案必定具有相同的哈希值，也就是相同的唯一標誌；不同的檔案在很大概率上是具有不同的哈希值唯一標誌的；
#即使真的遇到了散列衝突，我們可以再詳細比對兩個文件的全部二進位數據，進一步判斷它們是否是同一個文件，這個事件發生的機率太小了。但這種方案既保證了高效，又保證了可靠。
這種應用場景用到了哈希演算法的特性2和3。
在P2P下載協定中，我們會從不同的機器上下載同一部電影的不同部分，然後在自己的機器上組裝影片。如果這其中某個部分的電影下載過程中出了錯誤或內容被竄改了，就可能導致下載出錯或中病毒。
因此，我們先對所有部分進行hash計算，並保存在種子檔案中。等到所有部分下載完成，我們將所有部分進行雜湊計算得到雜湊值，再和種子檔案中的進行比較，以此來校驗檔案是否完整。
這種應用場景用到了哈希演算法的特性2和4。
這種場景在前面講過散列表的時候就已經介紹過了。這種場景下，對特點1要求不是很高，特點2的要求是散列值要盡量均勻分佈，特點3也在一定程度上可以接受衝突，使用開放尋址法和拉鍊法就可以解決，就是特點4要求高一點，需要追求性能。
負載平衡的演算法有很多，例如輪詢、隨機、加權輪詢等，但是目標是要實現一個會話黏滯的負載平衡演算法，即同一個客戶端在一個會話期間所有的請求都是路由到同一台伺服器的。
我們可以將客戶端的IP或會話ID進行哈希計算，得到的哈希值與伺服器個數進行取模運算，最終得到的值就是需要路由的伺服器，這樣就能實現會話粘滯的目的。
當我們需要處理海量數據的時候，單一伺服器無法載入和計算如此海量的數據，那麼我們就需要將海量數據均勻地分給N台伺服器進行平行計算，如何將資料均勻分給N台伺服器呢？
我們對資料進行雜湊計算，用得到的雜湊值對伺服器個數N取模，相同結果的資料會被分到相同的伺服器上，交給這台伺服器處理。 N台伺服器並行處理大量數據，最終再將結果合併即可。
將海量資料儲存到分散式快取或分散式資料庫中，借用的想法和上面的資料分片是類似的。只不過，原先設定好的伺服器數量不夠的時候該如何處理呢？
並不是簡單地加幾台機器就能解決的，這會破壞雜湊值的取模運算，導致快取穿透，造成雪崩效應。同理，當某個機器故障被移除時也會導致相同的問題。這個時候需要藉助一致性雜湊演算法來解決這個問題。
一致性雜湊演算法簡單來說就是建構一個hash環，環上有2^32個節點，將伺服器IP和檔案都hash計算映射到對應的節點上。所有文件順時針遇到的第一台伺服器就當作自己存放的伺服器。如此，增加或刪除某伺服器的時候，影響的檔案數量就可控，不會造成全域雪崩。
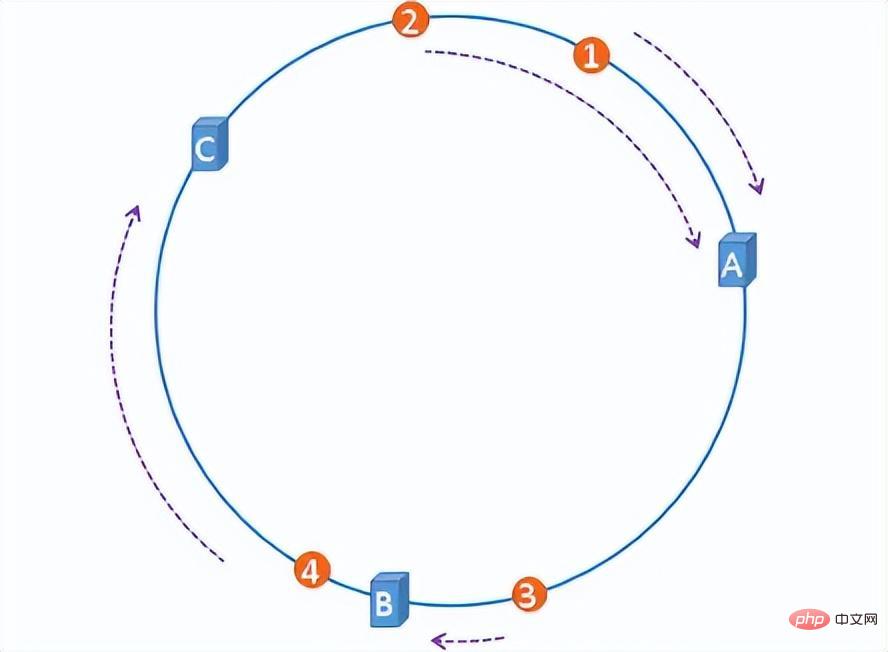
hash環
但是，在一定機率上，伺服器IP在映射到hash環上時，會出現hash環偏斜的問題，此時會導致伺服器上檔案分佈極為不均勻，退化為一開始在增刪伺服器時容易造成雪崩效應的場景。
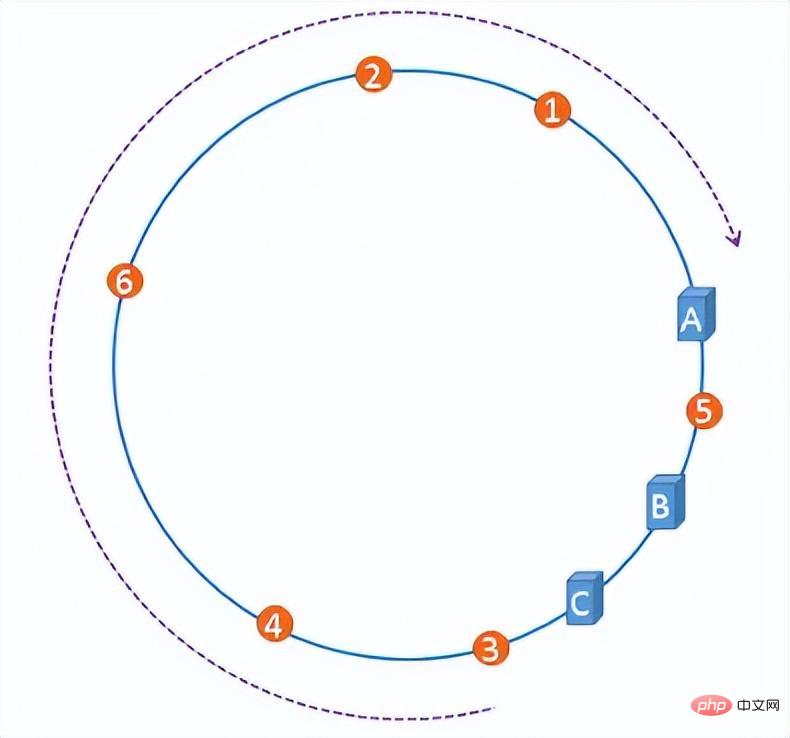
hash環的偏斜
我們可以人為地為這些伺服器增加若干虛擬節點，使得所有伺服器節點在hash環上分佈均勻。
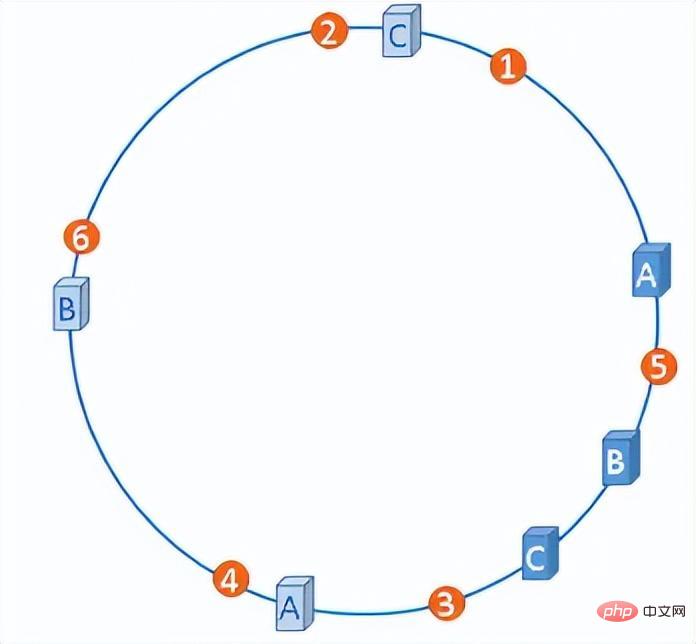
帶有虛擬節點的hash環
Hash演算法的使用場景遠不止上述這些，還有例如CRC校驗。
以上是一文搞懂Hash演算法以及應用場景的詳細內容。更多資訊請關注PHP中文網其他相關文章！
