本文為來自 位元組教育-成人與創新前端團隊 成員的文章,已授權 ELab 發佈。
本文使用機器學習、餘弦相似度判定法等方法,設計與驗證實現了滑鼠手勢的辨識方案,並嘗試將方案推廣到三維空間。
端技術的核心內容是直接回應使用者的互動。基本的邏輯是,在特定的平台下均存在一些預先定義的互動事件,使用者特定的互動動作會觸發對應的互動事件。整個使用者產品的互動設計也都是基於此去開展的。為了達到良好的使用者體驗,便捷的互動是必要的。
在PC端場景,滑鼠(觸控板)是除了鍵盤外最重要的輸入設備,常見的滑鼠操作就是滑鼠上自帶的按鍵與滾輪,於是對應的常用互動事件也就是點擊、滾動、拖動,而這些互動都需要有一個物件(例如點擊某個button,滾動某個內容區或整個視區、拖曳某個圖片),不如快捷鍵那麼方便。然而在特定場景下,快捷鍵也沒有滑鼠那麼便捷,所以期望滑鼠也有快捷操作。滑鼠手勢就是一個相對小眾但方便好用的快速操作。常見的滑鼠手勢有劃直線、打鉤、畫圓圈等。在早期瀏覽器百家齊放的年代,為了差異化競爭優勢,許多國產瀏覽器將便捷的滑鼠手勢操作作為一大賣點,那時手勢操作就逐漸得到了廣泛的支持與應用,默默培養了市場與用戶習慣。
在行動裝置觸控螢幕場景,手勢操作的優勢更加明顯,手勢操作就演變成了經典的「左滑後退」、「右劃前進」、「上劃回首頁」、「下劃刷新/喚起通知/喚起控制中心」。
最近VR/AR/MR興起後,三維空間裡的手勢操作得到進一步推廣應用。
因此,我們以PC端為例,實現滑鼠手勢的識別,講清楚互動手勢的核心實現邏輯,並以此類推,嘗試將方案推廣到更多端場景。
平移和縮放不變形,也就是手勢路徑整體的位置和大小不重要。
對使用者的重複手勢有一定的包容度。
該問題特殊的地方在於對不確定性的處理,使用者劃出的滑鼠手勢存在不確定性。
對於預設了標準路徑的情況,問題就轉換成了偵測「預設的確定性路徑」與「使用者輸入的不確定性的路徑」的相似性。
對於使用者自訂路徑的情況,問題就轉換成了偵測「使用者設定的不確定性的路徑」與「使用者輸入的不確定性的路徑」的相似性。
如果依照傳統的程式設計模型,那必須要求程式邏輯縝密,對條件判斷定下清晰的規則、去精確衡量這種不確定性。也就是需要一種“魔法運算”,把兩條路徑代入,就能得到它們是否相似的結果。
針對手勢本身,我們可以把它看成一張普通的柵格圖像,也可以把它看成一個向量圖形。對於柵格圖像,我們可以利用經典機器學習的方法來判斷圖像的分類而不必理解圖片的內容是什麼。對於向量圖形,我們需要為此定義一個特殊的資料結構,並深入研究圖形的相似性的表徵量。我們接下來的實作就從這兩個思路分別展開。
首先需要改變思考方式。機器學習的程式設計和傳統程式設計的思考方式完全不同。剛才提到,傳統程式設計要求程式邏輯例如條件判斷、循環等流程都做出精確地人為規定和編碼。機器學習程式設計不再拘泥於制定和編寫細緻的邏輯規則,而是建構神經網路讓電腦進行特徵的學習。
機器學習的關鍵是大量且可靠的資料集,這個label工作非常耗時,為了驗證可行性,我們使用相似的手寫數位資料集mnist來取代真實的手勢場景。
因此,接下來我們的步驟就是:
機器學習的演算法和模型眾多,需要針對不同領域選擇。 Tensorflow.js官方提供了一系列預先訓練好的模型[1],可以直接使用或重新訓練並使用。
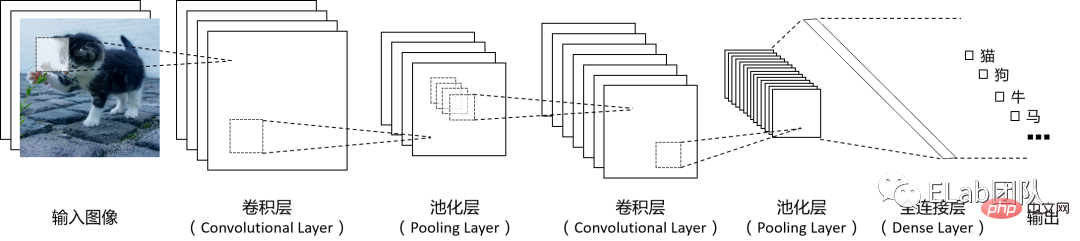
卷積神經網路CNN(Convolutional Neural Networks) 是應用非常廣泛的機器學習模型,尤其在處理圖片或其他具有柵格特徵的資料時具有非常好的表現。在資訊處理時,CNN將像素的行列空間結構作為輸入,透過多個數學計算層來進行特徵提取,然後再將訊號轉換為特徵向量將其連接到傳統神經網路的結構中,經過特徵提取的圖像所對應的特徵向量在提供給傳統神經網路時體積更小,需要訓練的參數數量也會相應減少。卷積神經網路的基本運作原理圖如下(圖中各層的數量可以按需設計):
資料集
/** * @license* Copyright 2018 Google LLC. All Rights Reserved. * Licensed under the Apache License, Version 2.0 (the "License"); * you may not use this file except in compliance with the License. * You may obtain a copy of the License at * * http://www.apache.org/licenses/LICENSE-2.0 * * Unless required by applicable law or agreed to in writing, software * distributed under the License is distributed on an "AS IS" BASIS, * WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. * See the License for the specific language governing permissions and * limitations under the License. * ============================================================================= */
const IMAGE_SIZE = 784;
const NUM_CLASSES = 10;
const NUM_DATASET_ELEMENTS = 65000;
const NUM_TRAIN_ELEMENTS = 55000;
const NUM_TEST_ELEMENTS = NUM_DATASET_ELEMENTS - NUM_TRAIN_ELEMENTS;
const MNIST_IMAGES_SPRITE_PATH =
'https://storage.googleapis.com/learnjs-data/model-builder/mnist_images.png';
const MNIST_LABELS_PATH =
'https://storage.googleapis.com/learnjs-data/model-builder/mnist_labels_uint8';
/** * A class that fetches the sprited MNIST dataset and returns shuffled batches. * * NOTE: This will get much easier. For now, we do data fetching and * manipulation manually. */export class MnistData {
constructor() {
this.shuffledTrainIndex = 0;
this.shuffledTestIndex = 0;
}
async load() {
// Make a request for the MNIST sprited image.const img = new Image();
const canvas = document.createElement('canvas');
const ctx = canvas.getContext('2d');
const imgRequest = new Promise((resolve, reject) => {
img.crossOrigin = '';
img.onload = () => {
img.width = img.naturalWidth;
img.height = img.naturalHeight;
const datasetBytesBuffer =
new ArrayBuffer(NUM_DATASET_ELEMENTS * IMAGE_SIZE * 4);
const chunkSize = 5000;
canvas.width = img.width;
canvas.height = chunkSize;
for (let i = 0; i < NUM_DATASET_ELEMENTS / chunkSize; i++) {
const datasetBytesView = new Float32Array(
datasetBytesBuffer, i * IMAGE_SIZE * chunkSize * 4,
IMAGE_SIZE * chunkSize);
ctx.drawImage(
img, 0, i * chunkSize, img.width, chunkSize, 0, 0, img.width,
chunkSize);
const imageData = ctx.getImageData(0, 0, canvas.width, canvas.height);
for (let j = 0; j < imageData.data.length / 4; j++) {
// All channels hold an equal value since the image is grayscale, so// just read the red channel.datasetBytesView[j] = imageData.data[j * 4] / 255;
}
}
this.datasetImages = new Float32Array(datasetBytesBuffer);
resolve();
};
img.src = MNIST_IMAGES_SPRITE_PATH;
});
const labelsRequest = fetch(MNIST_LABELS_PATH);
const [imgResponse, labelsResponse] =
await Promise.all([imgRequest, labelsRequest]);
this.datasetLabels = new Uint8Array(await labelsResponse.arrayBuffer());
// Create shuffled indices into the train/test set for when we select a// random dataset element for training / validation.this.trainIndices = tf.util.createShuffledIndices(NUM_TRAIN_ELEMENTS);
this.testIndices = tf.util.createShuffledIndices(NUM_TEST_ELEMENTS);
// Slice the the images and labels into train and test sets.this.trainImages =
this.datasetImages.slice(0, IMAGE_SIZE * NUM_TRAIN_ELEMENTS);
this.testImages = this.datasetImages.slice(IMAGE_SIZE * NUM_TRAIN_ELEMENTS);
this.trainLabels =
this.datasetLabels.slice(0, NUM_CLASSES * NUM_TRAIN_ELEMENTS);
this.testLabels =
this.datasetLabels.slice(NUM_CLASSES * NUM_TRAIN_ELEMENTS);
}
nextTrainBatch(batchSize) {
return this.nextBatch(
batchSize, [this.trainImages, this.trainLabels], () => {
this.shuffledTrainIndex =
(this.shuffledTrainIndex + 1) % this.trainIndices.length;
return this.trainIndices[this.shuffledTrainIndex];
});
}
nextTestBatch(batchSize) {
return this.nextBatch(batchSize, [this.testImages, this.testLabels], () => {
this.shuffledTestIndex =
(this.shuffledTestIndex + 1) % this.testIndices.length;
return this.testIndices[this.shuffledTestIndex];
});
}
nextBatch(batchSize, data, index) {
const batchImagesArray = new Float32Array(batchSize * IMAGE_SIZE);
const batchLabelsArray = new Uint8Array(batchSize * NUM_CLASSES);
for (let i = 0; i < batchSize; i++) {
const idx = index();
const image =
data[0].slice(idx * IMAGE_SIZE, idx * IMAGE_SIZE + IMAGE_SIZE);
batchImagesArray.set(image, i * IMAGE_SIZE);
const label =
data[1].slice(idx * NUM_CLASSES, idx * NUM_CLASSES + NUM_CLASSES);
batchLabelsArray.set(label, i * NUM_CLASSES);
}
const xs = tf.tensor2d(batchImagesArray, [batchSize, IMAGE_SIZE]);
const labels = tf.tensor2d(batchLabelsArray, [batchSize, NUM_CLASSES]);
return {xs, labels};
}
} // 我们直接使用mnist数据集这个经典的手写数字数据集,节约了收集手写数字的創造屬於你自己的互動事件-螢幕手勢識別集的时间
import {MnistData} from './data.js';
let cnnModel=null;
async function run() {
// 加载数据集 const data = new MnistData();
await data.load();
// 构造模型,设置模型参数 cnnModel = getModel();
// 训练模型 await train(cnnModel, data);
}
function getModel() {
const model = tf.sequential();
const IMAGE_WIDTH = 28;
const IMAGE_HEIGHT = 28;
const IMAGE_CHANNELS = 1;
// 在第一层,指定输入数据的形状,设置卷积参数 model.add(tf.layers.conv2d({
// 流入模型第一层的数据的形状。在本例中,我们的 MNIST 示例是 28x28 像素的黑白創造屬於你自己的互動事件-螢幕手勢識別。創造屬於你自己的互動事件-螢幕手勢識別数据的规范格式为 [row, column, depth] inputShape: [IMAGE_WIDTH, IMAGE_HEIGHT, IMAGE_CHANNELS],
// 要应用于输入数据的滑动卷积过滤器窗口的尺寸。在此示例中,我们将kernelSize设置成5,也就是指定 5x5 的卷积窗口。 kernelSize: 5,
// 尺寸为 kernelSize 的过滤器窗口数量 filters: 8,
// 滑动窗口的步长,即每次移动創造屬於你自己的互動事件-螢幕手勢識別时过滤器都会移动多少像素。我们指定步长为 1,表示过滤器将以 1 像素为步长在創造屬於你自己的互動事件-螢幕手勢識別上滑动。 strides: 1,
// 卷积完成后应用于数据的激活函数。在本例中,我们将应用修正线性单元 (ReLU) 函数,这是机器学习模型中非常常见的激活函数。 activation: 'relu',
// 通常使用 VarianceScaling作为随机初始化模型权重的方法 kernelInitializer: 'varianceScaling'
}));
// MaxPooling最大池化层使用区域最大值而不是平均值进行降采样 model.add(tf.layers.maxPooling2d({poolSize: [2, 2], strides: [2, 2]}));
// 重复一遍conv2d + maxPooling // 注意这次卷积的过滤器窗口数量更多 model.add(tf.layers.conv2d({
kernelSize: 5,
filters: 16,
strides: 1,
activation: 'relu',
kernelInitializer: 'varianceScaling'
}));
model.add(tf.layers.maxPooling2d({poolSize: [2, 2], strides: [2, 2]}));
// 现在我们将2维滤波器的输出展平为1维向量,作为最后一层的输入。这是将高维数据输入给最后的分类输出层时的常见做法。 // 創造屬於你自己的互動事件-螢幕手勢識別是高维数据,而卷积运算往往会增大传入其中的数据的大小。在将数据传递到最终分类层之前,我们需要将数据展平为一个长数组。密集层(我们会用作最终层)只需要采用 tensor1d,因而此步骤在许多分类任务中很常见。 // 注意:展平层中没有权重。它只是将其输入展开为一个长数组。 model.add(tf.layers.flatten());
// 计算我们的最终概率分布,我们将使用密集层计算10个可能的类的概率分布,其中得分最高的类将是预测的数字。 const NUM_OUTPUT_CLASSES = 10;
model.add(tf.layers.dense({
units: NUM_OUTPUT_CLASSES,
kernelInitializer: 'varianceScaling',
activation: 'softmax'
}));
// 模型编译,选择优化器,损失函数categoricalCrossentropy,和精度指标accuracy(正确预测在所有预测中所占的百分比),然后编译并返回模型 const optimizer = tf.train.adam();
model.compile({
optimizer: optimizer,
loss: 'categoricalCrossentropy',
metrics: ['accuracy'],
});
return model;
}
// 我们的目标是训练一个模型,该模型会获取一张創造屬於你自己的互動事件-螢幕手勢識別,然后学习预测創造屬於你自己的互動事件-螢幕手勢識別可能所属的 10 个类中每个类的得分(数字 0-9)。 async function train(model, data) {
const metrics = ['loss', 'val_loss', 'acc', 'val_acc'];
const container = {
name: 'Model Training', tab: 'Model', styles: { height: '1000px' }
};
const fitCallbacks = tfvis.show.fitCallbacks(container, metrics);
const BATCH_SIZE = 512;
const TRAIN_DATA_SIZE = 5500;
const TEST_DATA_SIZE = 1000;
const [trainXs, trainYs] = tf.tidy(() => {
const d = data.nextTrainBatch(TRAIN_DATA_SIZE);
return [
d.xs.reshape([TRAIN_DATA_SIZE, 28, 28, 1]),
d.labels
];
});
const [testXs, testYs] = tf.tidy(() => {
const d = data.nextTestBatch(TEST_DATA_SIZE);
return [
d.xs.reshape([TEST_DATA_SIZE, 28, 28, 1]),
d.labels
];
});
// 设置特征和标签 return model.fit(trainXs, trainYs, {
batchSize: BATCH_SIZE,
validationData: [testXs, testYs],
epochs: 10, //训练轮次 shuffle: true,
callbacks: fitCallbacks
});
} // 预测canvas上画的图形属于哪个分类 function predict(){
const input = tf.tidy(() => {
return tf.image
.resizeBilinear(tf.browser.fromPixels(canvas), [28, 28], true)
.slice([0, 0, 0], [28, 28, 1])
.toFloat()
.div(255)
.reshape([1, 28, 28, 1]);
});
const pred = cnnModel.predict(input).argMax(1);
console.log('预测结果为', pred.dataSync())
alert(`预测结果为 ${pred.dataSync()[0]}`);
};
document.getElementById('predict-btn').addEventListener('click', predict)
document.getElementById('clear-btn').addEventListener('click', clear)
document.addEventListener('DOMContentLoaded', run);
const canvas = document.querySelector('canvas');
canvas.addEventListener('mousemove', (e) => {
if (e.buttons === 1) {
const ctx = canvas.getContext('2d');
ctx.fillStyle = 'rgb(255,255,255)';
ctx.fillRect(e.offsetX, e.offsetY, 10, 10);
}
});
function clear(){
const ctx = canvas.getContext('2d');
ctx.fillStyle = 'rgb(0,0,0)';
ctx.fillRect(0, 0, 300, 300);
};
clear();向量的相似度通常使用余弦相似度来度量,即计算向量夹角的余弦值。将两组数据两两对应,分成128组向量,每组2个,计算每组向量的余弦值并累加。最终得到的结果应该会在 [-128, 128] 之间,数值越大也就表示相似度越高。我们只需设置一个阈值,超过这个阈值的就认为匹配成功。
为了计算两个向量夹角的余弦值,引入向量的点乘,根据向量点乘公式(推导过程[3]):

这里|a|表示向量a的模(长度),θ表示两个向量之间的夹角。
两个互相垂直的向量的点积总是零。若向量a和b都是单位向量(长度为1),它们的点积就是它们的夹角的余弦。那么,给定两个向量,它们之间的夹角可以通过下列公式得到:

这个运算可以简单地理解为:在点积运算中,第一个向量投影到第二个向量上(这里,向量的顺序是不重要的,点积运算是可交换的),然后通过除以它们的标量长度来“标准化”。这样,这个分数一定是小于等于1的,可以简单地转化成一个角度值。
对于二维向量,我们用一个[number, number]元组来表示。
核心实现逻辑:
import { useEffect, useState, useRef, useMemo } from 'react'
import throttle from "lodash/throttle"
type Position = {x:number, y:number};
type Vector = [number, number];
// 预先定义特殊V字型的手势路径,便于调试。 const shapeVectors_v: Vector[] = [[5,16],[13,29],[4,9],[6,9],[8,8],[1,0],[1,0],[1,-2],[0,-3],[7,-11],[21,-34],[10,-19]];
const shapeVectors_l: Vector[] = [[0,15],[0,33],[0,19],[0,4],[0,3],[0,8],[2,6],[11,0],[28,0],[18,0],[5,0],[1,0]]
const shapeVectors_6: Vector[] = [[-41,18],[-40,33],[-30,39],[-24,62],[1,53],[40,27],[38,2],[30,-34],[7,-41],[-31,-21],[-38,-4],[-19,0]];
const shapeVectors: {[key:string]: Vector[]} = {
v: shapeVectors_v,
l: shapeVectors_l,
6: shapeVectors_6
}
function Gesture(){
const pointsRef = useRef<Position[]>([]);
const sparsedPointsRef = useRef<Position[]>([]);
const vectorsRef = useRef<Vector[]>([]);
const canvasContextRef = useRef<CanvasRenderingContext2D>()
const containerRef = useRef<HTMLDivElement>(null)
const [predictResults, setPredictResults] = useState<{label: string, similarity: number}[]>([])
// 按一定的时间间隔采集点 const handleMouseMoveThrottled = useMemo(()=>{return throttle(handleMouseMove, 16)}, [canvasContextRef.current])
useEffect(()=>{
const canvasEle = document.getElementById('canvas-ele') as HTMLCanvasElement;
const ctx = canvasEle.getContext('2d')!;
canvasContextRef.current=ctx;
handleClear();
}, [])
function handleMouseDown(){
containerRef?.current?.addEventListener('mousemove', handleMouseMoveThrottled);
}
function handleMouseUp(){
console.log('up')
containerRef?.current?.removeEventListener('mousemove', handleMouseMoveThrottled);
console.log('points', sparsedPointsRef.current)
console.log('vectors', JSON.stringify(vectorsRef.current))
pointsRef.current=[]
}
// 为了方便示意,我们把鼠标路径可视化出来。 function drawPoint(x:number,y:number){
// console.log(x, y) // canvasContext?.arc(x, y, 5, 0, Math.PI*2); (canvasContextRef.current!).fillStyle = 'red';
canvasContextRef.current?.fillRect(x, y, 10,10)
}
// 鼠标滑过时,记录下一串间隔的点。 function handleMouseMove(e: any){
const x:number = e.offsetX, y:number = e.offsetY;
drawPoint(x, y)
const newPoints = [...pointsRef.current, {x,y}];
pointsRef.current = newPoints;
const sparsedNewPoints = sparsePoints(newPoints);
sparsedPointsRef.current=sparsedNewPoints;
const vectors = points2Vectors(sparsedNewPoints)
vectorsRef.current = vectors;
console.log('points', x, y)
// const angles = vectors.map(vector2PolarAngle) // console.log('angles', angles[angles.length-1]) }
// 如果点太多,处理起来性能不佳,除了节流之外,我们始终将点抽稀到13个(我们假设每个手势的持续时间都不低于200ms,能保证在节流16ms的情况下,至少收集到13个原始点,这样抽稀才有意义) // 抽稀的策略是以固定的间隔平均抽,这样有个潜在问题:如果用户划手势时速度不够均匀,比如在同一个手势路径中某段时间划的速度比较快(点会比较密集),在某段时间的速度比较慢(点会比较稀疏),那由抽稀后的点构造出的路径向量就会比较失真,影响最终判断的准确性。 // 优化的方案是在空间上采用分区抽稀的策略,避免用户手速不均匀导致的问题,但分区逻辑比较复杂,我们暂且按下不做深入研究。 // todo: 抽稀后,相邻的点不能重复,否则会有0向量、对运算和判断造成干扰。 function sparsePoints(points: Position[]){
const sparsedLength = 13;
if(points.length<=sparsedLength){
return points;
}else{
let sparsedPoints = [];
let step = points.length/sparsedLength;
for(let i=0; i<sparsedLength; i++){
const curIndex = Math.round(step*i);
sparsedPoints.push(points[curIndex])
}
return sparsedPoints;
}
}
// 对于非闭合的路径,手势方向会影响判断逻辑,相同的路径可能是由相反的手势方向画出来的。比如L形的手势。 // 对于闭合的路径,手势的方向和起止位置都会影响判断逻辑,相同的路径可能是由相反的手势方向画出来的,也可能是由不同起始位置画出来的。比如圆形的手势。 // 为了消除相同路径不同画法的影响,我们做如下处理
function normalizePoints(points:Position[]){
// if (是闭合路径) 将位置在最左上角的点作为数组的第一位,其余的依次排列,然后返回 // else 原样返回 return points;
}
// 相邻的两个点相连,生成一个向量。用这n个点的坐标生成n-1个向量,这n-1个向量组成一段路径,用来表示一个鼠标手势。 function points2Vectors(points: Position[]){
if(points.length<=1){
return []
}else{
return points.reduce((pre:Vector[], cur, curIdx)=>{
if(curIdx===0){return []}
const prePoint = points[curIdx-1];
const vec:Vector = [cur.x-prePoint.x, cur.y-prePoint.y];
return [...pre, vec];
}, [])
}
}
// 判断两条路径是否是相同,保证组成两条路径的向量数相同,然后计算两条路径对应向量的余弦相似度(取值在-1~1之间,越接近-1或者1,越相似)。最后再与定义的阈值比较,超过阈值就认为路径相同。 function judge(vec1:Vector[], vec2: Vector[], threshold?:number){
// 暂定阈值为0.5 const finalThreshold = threshold||0.5;
// 为消除路径方向的影响(一个向量与另一个反向相反的向量的余弦值是-1,应该认为它们形状相同),反转路径后再次判断 return cosineSimilarity(vec1, vec2)>=finalThreshold || cosineSimilarity(vec1, vec2.reverse())>=finalThreshold
}
// 两组向量的余弦相似度,保证组成两条路径的向量数相同,然后计算两条路径对应向量的余弦值,累加取均值.取值在-1~1之间,越接近-1或者1,越相似. function cosineSimilarity(vec1: Vector[], vec2: Vector[]){
if(vec1.length!==vec2.length){
console.warn('进行比较的两个路径长度(路径内的向量数)必须一致')
return 0;
}else{
let cosValueSum = 0;
vec1.forEach((v1, i)=>{
cosValueSum+=vectorsCos(v1, vec2[i])
})
// 取余弦值的绝对值,绝对值越接近1,相似度越高。 const cosValueRate = Math.abs(cosValueSum/vec1.length);
console.log('cosValueRate', cosValueRate)
return cosValueRate;
}
}
// 两个向量的余弦值 function vectorsCos(v1:Vector, v2:Vector){
// 特殊情况,0向量的余弦值我们认为是1 if(vectorLength(v1)*vectorLength(v2)===0){
return 1;
}
return vectorsDotProduct(v1, v2)/(vectorLength(v1)*vectorLength(v2));
}
// 向量的点乘 function vectorsDotProduct(v1:Vector, v2:Vector){
return v1[0]*v2[0]+v1[1]*v2[1];
}
// 向量的长度 function vectorLength(v:Vector){
return Math.sqrt(Math.pow(v[0], 2)+Math.pow(v[1], 2))
}
// 向量归一化,消除向量在长度上的差异,控制变量,方便训练机器学习模型(https://zhuanlan.zhihu.com/p/424518359) function normalizeVector(vec:Vector){
const length = Math.sqrt(Math.pow(vec[0],2)+Math.pow(vec[1], 2))
return [vec[0]/length, vec[1]/length]
}
function handlePredict(){
const results = Object.keys(shapeVectors).map(key=>({
label: key,
similarity: cosineSimilarity(shapeVectors[key], vectorsRef.current),
}))
setPredictResults(results);
console.log('results', results)
}
function handleClear(){
pointsRef.current=[];
sparsedPointsRef.current=[];
vectorsRef.current=[];
(canvasContextRef.current!).fillStyle = 'rgb(0,0,0)';
(canvasContextRef.current!).fillRect(0, 0, 500, 500);
setPredictResults([]);
}
// 工程化封装,为某个dom元素增加自定义手势事件 function addCustomEvent(ele: HTMLElement, eventName: string, eventLisener:(...args:any[])=>any){
let points = [], sparsedPoints=[],vecs:Vector[]=[];
const customEvent = new Event(eventName);
function handleMouseMove(e: any){
const x:number = e.offsetX, y:number = e.offsetY;
const newPoints = [...pointsRef.current, {x,y}];
points = newPoints;
const sparsedNewPoints = sparsePoints(newPoints);
sparsedPoints=sparsedNewPoints;
const newVectors = points2Vectors(sparsedNewPoints)
vecs = newVectors;
console.log('points', x, y)
}
const handleMouseMoveThrottled = throttle(handleMouseMove, 16)
function handleMouseDown(){
ele.addEventListener('mousemove', handleMouseMoveThrottled);
}
function handleMouseUp(){
console.log('up')
ele.removeEventListener('mousemove', handleMouseMoveThrottled);
console.log('points', sparsedPointsRef.current)
console.log('vectors', JSON.stringify(vectorsRef.current))
if(judge(vecs, shapeVectors['l'], 0.6)){
ele.dispatchEvent(customEvent)
}
points=[], sparsedPoints=[], vecs=[];
}
ele.addEventListener(eventName, eventLisener)
ele.addEventListener('mousedown', handleMouseDown);
ele.addEventListener('mouseup', handleMouseUp);
return function distroyEventListener(){
ele.removeEventListener(eventName, eventLisener)
}
}
return
<canvas width='500' height="500"></canvas>
<section>
<button notallow={handlePredict}>预测</button>
<button notallow={handleClear}>清空</button>
</section>
<ul>
{predictResults.map(e=>(
<li key={e.label}>
{`与 ${e.label}的相似度:${e.similarity}`}
</li>
))}
</ul>
}
export default Gesture点和向量的计算属于计算密集型任务,且其需要与主线程通信的数据量不大,考虑将其搬进webworker。此外,canvas的渲染性能也可以使用requestAnimationFrame和硬件加速来优化。属于常见的工程层面优化,此处略。
余弦相似度的方法,优势在于计算量不大,可以在运行时由用户自定义手势,且所需保存的数据量不大,也适合网络传输。劣势在于难以衡量复杂多笔画、没有严格笔顺的图形的相似度。
针对二维平面内的手势识别方案如何扩展到三维空间呢?比如在VR/MR场景内,手势路径会是一组三维向量,如果我们能将余弦相似度的适用范围扩展到三维向量,也就顺理成章地解决了这个问题。
基本思路就是分别分析两个三维向量在xoy平面上的投影之间的夹角以及在yoz平面上的投影之间的夹角的余弦相似度,将两者的乘积作为两个三维向量之间的余弦相似度。判断逻辑与二维向量的一致。
综合考虑机器学习的方案和几何分析方案的优劣势,我们做如下设计。对于预设的手势,我们构造数据集、离线训练模型,然后将模型内置在产品内。对于自定义的手势,我们采用几何分析方案,让用户连续输入3次,先计算每次输入的路径的两两之间的相似度,且选出相似度的最小值n,如果最小值n大于某个阈值m,且每次输入的路径与其他已有路径的相似度均小于m时,我们就将距离其余两条路径的相似度之和最小的那条路径作为用户自定义的新路径,n作为其相似度判断的阈值。
参考资料
[1]预训练好的模型: https://github.com/tensorflow/tfjs-models
[2]环境搭建: https://github.com/tensorflow/tfjs#getting-started
[3]推导过程: https://blog.csdn.net/dcrmg/article/details/52416832
[4]复杂鼠标手势的识别是如何实现的? - 知乎: https://www.zhihu.com/question/20607813
[5]点积相似度、余弦相似度、欧几里得相似度: https://zhuanlan.zhihu.com/p/159244903
[6]机器学习并没有那么深奥,它还很有趣(1)-36氪: https://m.36kr.com/p/1721248956417
[7]计算向量间相似度的常用方法: https://cloud.tencent.com/developer/article/1668762
[8]C#手势库的核心逻辑实现: https://github.com/poerin/Stroke/blob/master/Stroke/Gesture.cs
[9]什么是张量 (tensor)? - 知乎: https://www.zhihu.com/question/20695804
[10]使用 CNN 识别手写数字: https://codelabs.developers.google.com/codelabs/tfjs-training-classfication?hl=zh-cn#0
[11]机器学习: https://zh.m.wikipedia.org/zh/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0
[12]文字识别方法整理(2015~2019): https://zhuanlan.zhihu.com/p/65707543
以上是創造屬於你自己的互動事件-螢幕手勢識別的詳細內容。更多資訊請關注PHP中文網其他相關文章!




