數學推理是人類智慧的關鍵體現，它使我們能夠理解並做出基於數值資料和語言的決策。數學推理適用於各個領域，包括科學、工程、金融和日常生活，並包含一系列能力，諸如從模式識別、數字運算等基本技能到解決問題、邏輯推理和抽象思維等高級技能。
長期以來，開發能夠解決數學問題、證明數學定理的 AI 系統是機器學習和自然語言處理領域的研究重點。這也可以追溯到 20 世紀 60 年代。
在深度學習興起的近十年，人們對這一領域的興趣更是大幅增長：
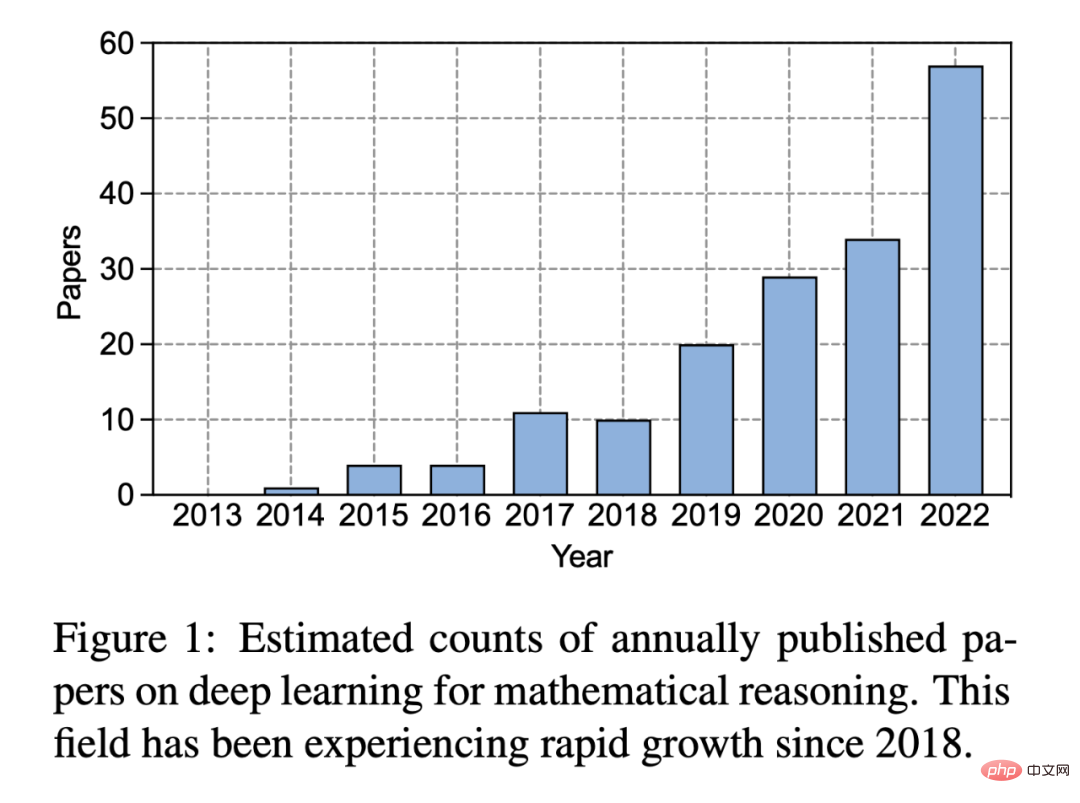
##圖1：每年發表的關於數學推理的深度學習論文的預估數量。自 2018 年以來，這一領域經歷了快速成長。
深度學習在各種自然語言處理任務中顯示出巨大的成功，如問題回答和機器翻譯。同樣，研究人員開發了各種用於數學推理的神經網路方法，這些方法在處理應用問題、定理證明和幾何問題解決等複雜任務時已被證明是有效的。例如，基於深度學習的應用題求解器採用了一個序列到序列的框架，並以注意力機製作為中間步驟產生數學表達式。此外，透過大規模語料庫和 Transformer 模型，預先訓練的語言模型在各種數學任務上取得了可喜的成果。最近，像 GPT-3 這樣的大型語言模型在複雜推理和語境學習中表現出令人印象深刻的能力，進一步推動了數學推理領域的發展。
在近期發布的一篇報告中，來自 UCLA 等機構的研究者係統回顧了深度學習在數學推理方面的進展。
論文連結：https://arxiv.org/pdf/2212.10535.pdf
#專案網址：https://github.com/lupantech/dl4math
#具體而言，本文討論了各種任務和資料集（第2 節），並研究了神經網路（第3 節）和預訓練語言模型（第4 節）在數學領域的進展。另外也探討了大型語言模型的脈絡學習在數學推理中的快速發展（第 5 節）。文章進一步分析了現有的基準，發現對多模態和低資源環境的關注較少（第 6.1 節）。基於實證的研究表明，目前的計算能力表徵是不充分的，深度學習方法在數學推理方面也是不一致的（第 6.2 節）。隨後，作者建議在概括性和魯棒性、可信推理、從回饋中學習和多模態數學推理方面改進目前的工作（第 7 節）。
任務和資料集本節研究了目前可用於研究使用深度學習方法的數學推理的各種任務和資料集，見表 2。
應用程式題(Math Word Problem)
應用程式題包含一個涉及人物、實體和數量的簡短敘述其，數學關係可以用一組方程式來模擬，方程式的解揭示了問題的最終答案。表 1 就是一個典型的例子。一個問題涉及加、減、乘、除四種基本的數學運算，有單一或多個運算步驟。應用題對 NLP 系統的挑戰在於對語言理解、語意解析和多種數學推理能力的需求。
#
現有的應用問題資料集涵蓋了小學階段的問題，這些問題是從線上學習網站上抓取的、從教科書中收集的或由人類手動註釋的。早期的應用題資料集相對較小，或僅限於少量的操作步驟。最近的一些數據集旨在增加問題的多樣性和難度。例如，目前最大的公開問題集 Ape210K 由 210k 個小學應用題組成；而 GSM8K 中的問題可以涉及多達 8 個步驟的解法。 SVAMP 是一個基準，測試深度學習模型對具有簡單變化的應用問題的穩健性。一些最近建立的資料集也涉及文字以外的模態。例如，IconQA 提供了一個抽象的圖表作為視覺背景，而 TabMWP 為每個問題提供了一個表格形式的背景。
大多數應用問題資料集會提供註釋方程式作為解的理由（如表 1）。為了提高學習的求解器的效能和可解釋性，MathQA 以精確的運算程式進行註釋，MathQA-Python 則提供具體的 Python 程式。另一些資料集用多步驟的自然語言解決方案對問題進行註釋，這些解決方案被認為更適合人類閱讀。 Lila 用 Python 程式的原理註解了許多前面提到的應用問題資料集。
理論證明
#定理證明自動化是 AI 領域的長期挑戰。問題通常是透過一連串的邏輯論證來證明一個數學定理的真理性。定理證明涉及各種技能，如選擇高效的多步驟策略、使用背景知識以及進行符號運算（如算術或推導）。
最近，人們對在形式化的互動式定理證明器（ITP）中使用語言模型進行定理證明越來越感興趣。定理會在 ITP 的程式語言中被陳述，然後透過產生「證明步驟」來簡化，直到它被簡化為已知事實。其結果是一個步驟序列，構成一個驗證的證明。
非形式化定理證明提出了定理證明的另一種媒介，即用自然語言和「標準」數學符號（如LATEX）的混合形式來編寫語句和證明，並由人類檢查其正確性。
一個新興的研究領域旨在結合非正式和正式定理證明的要素。例如，Wu et al. (2022b) 探索將非形式化語句翻譯成形式化語句，而Jiang et al. （2022b）發布了一個新版本的miniF2F 基準，其中增加了非形式化語句和證明，稱為miniF2F informal。 Jiang et al.（2022b） 探討將提供（或產生）的非形式化證明轉化為形式化證明。
幾何問題
#幾何問題自動化求解（GPS）也是數學推理研究中一個長期存在的人工智慧任務，並在近年來引起了廣泛關注。與應用題不同，幾何問題由自然語言的文字描述和幾何圖形組成。如圖 2 所示，多模態輸入描述了幾何元素的實體、屬性和關係，而目標是找到未知變數的數值解。由於需要複雜的技能，GPS 對深度學習方法來說是一項具有挑戰性的任務。它涉及解析多模態資訊、進行符號抽象、利用定理知識和進行定量推理的能力。
早期的資料集促進了這一領域的研究，然而這些資料集相對較小或不公開，這限制了深度學習方法的發展。為了應對這一限制，Lu et al. 創建了 Geometry3K 資料集，該資料集由 3002 個多選幾何問題組成，並對多模態輸入進行了統一的邏輯形式註釋。最近，更大規模的資料集，如 GeoQA、GeoQA 和 UniGeo 已經被引入，並被註釋了可以被神經求解器學習並執行以獲得最終答案的程式。
數學問答
最近的研究表明，SOTA 數學推理系統在推理上可能存在“脆性”，即模型依靠特定數據集的虛假信號和即插即用的計算來達到“令人滿意”的性能。為了解決這個問題，人們從各個方面提出了新的基準。 The Mathematics (Saxton et al., 2020) 資料集包含許多不同類型的數學問題，涵蓋算術、代數、機率和微積分。此資料集可以測量模型的代數泛化能力。同樣，MATH (Hendrycks et al., 2021) 由具有挑戰性的競賽數學組成，以衡量模型在複雜情況下的問題解決能力。
一些工作在問題輸入中加入了表格背景。例如，FinQA、TAT-QA 和 MultiHiertt 收集了需要表格理解和數值推理來回答的問題。一些研究則提出了大規模的數值推理的統一基準。 NumGLUE (Mishra et al., 2022b) 是一個多任務基準，目標是評估模型在八個不同任務上的表現。 Mishra et al. 2022a 提出了 Lila，進一步推動了這一方向，Lila 由 23 個數值推理任務組成，跨越了廣泛的數學主題、語言複雜性、問題格式和背景知識要求。
AI 同樣在其他類型的量化問題上有所成就。例如數字、圖表和繪圖，是以簡潔的方式傳達大量訊息的基本媒介。 FigureQA、DVQA、MNS、PGDP5K 和 GeoRE 都是為了研究模型對基於圖表的實體間的定量關係進行推理的能力推出的。 NumerSense 研究了現有的預訓練語言模型是否以及在多大程度上能夠感應數值常識知識。 EQUATE 在自然語言推理框架中對定量推理的各個方面進行了形式化。定量推理也經常出現在金融、科學和程式設計等特定領域。例如，ConvFinQA 以對話式問答的形式對財務報告進行數字推理；ScienceQA 涉及科學領域的數字推理；而 P3 研究了深度學習模型的函數推理能力，找到一個有效的輸入讓給定的程序返回 True。
對於常見的用於數學推理的幾種神經網絡，本文的作者也進行了總結。
Seq2Seq 網路
#Seq2Seq 神經網路已成功地應用於數學推理任務，如應用問題、定理證明、幾何問題和數學問題回答。 Seq2Seq 模型使用編碼器 - 解碼器架構，通常將數學推理形式化為一個序列生成任務。這種方法的基本概念是將輸入序列（如數學問題）映射到輸出序列（如方程式、程序和證明）。常見的編碼器和解碼器包括長短時記憶網路（LSTM）、門控遞歸單元（GRU）。大量的工作表明，Seq2Seq 模型比以前的統計學習方法具有性能優勢，包括它們的雙向變體 BiLSTM 和 BiGRU。 DNS 是第一個使用 Seq2Seq 模型將應用題中的句子轉換為數學方程式的工作。
基於圖的網路
#Seq2Seq 方法具備產生數學表達式和不依賴手工製作特徵的優點。數學表達式可以轉換為基於樹的結構，例如抽象語法樹（AST）和基於圖的結構，描述了表達式中的結構化資訊。然而，這種重要的資訊並沒有被 Seq2Seq 方法明確地建模。為了解決這個問題，研究者開發了基於圖的神經網路來明確地模擬表達式中的結構。
Sequence-to-tree（Seq2Tree）模型在輸出序列編碼時明確地對樹結構進行建模。例如，Liu et al. 設計了一個 Seq2Tree 模型來更好地利用方程式的 AST 資訊。相反，Seq2DAG 在生成方程式時應用了一個序列圖（Seq2Graph）框架，因為圖解碼器能夠提取多個變數之間的複雜關係。在對輸入的數學序列進行編碼時，也可以嵌入基於圖的資訊。例如，ASTactic 在 AST 上應用 TreeLSTM 來表示定理證明的輸入目標和前提。
基於注意力的網路
注意力機制已成功應用於自然語言處理和電腦視覺問題，在解碼處理過程中考慮了輸入的隱藏向量。研究人員一直在探索它在數學推理任務中的作用，因為它可以用來識別數學概念之間最重要的關係。例如，MATH-EN 是一個應用題求解器，它得益於透過自註意力學習的長距離依賴資訊。基於注意力的方法也被應用於其他數學推理任務，如幾何問題和定理證明。為了提取更好的表徵，人們研究了各種注意力機制，例如使用不同的多頭注意力來提取各種類型的 MWP 特徵的 Group-ATT，以及被應用於提取 knowledge-aware 資訊的圖注意。
其他神經網路
#數學推理任務的深度學習方法也可以利用其他神經網絡，如卷積神經網路和多模態網路。一些工作使用卷積神經網路架構對輸入文字進行編碼，使模型有能力捕捉輸入中符號之間的長期關係。例如，Irving et al. 研究提出了深度神經網路在定理證明中的第一個應用，它依靠卷積網路在大型理論中進行前提選擇。
多模態數學推理任務，如幾何問題解決和基於圖表的數學推理，被形式化為視覺問題答案（VQA）問題。在這個領域，視覺輸入使用 ResNet 或 Faster-RCNN 進行編碼，而文字表徵則透過 GRU 或 LTSM 獲得。隨後，使用多模態融合模型學習聯合表徵，如 BAN、FiLM 和 DAFA。
其他深度神經網路結構也可用於數學推理。 Zhang et al. 利用圖譜神經網路（GNN）在空間推理中的成功，將其用於幾何問題。由於能夠解決縱向時間序列數據，WaveNet 被應用於定理證明。此外，在 DDT 中產生數學方程式方面，Transformer 被發現優於 GRU。以及，MathDQN 是第一個探索解決數學應用題的強化學習工作，主要利用其強大的搜尋能力。
預訓練的語言模型已經在廣泛的NLP 任務上表現出顯著的性能提升，同樣應用於數學相關的問題，先前的工作表明，預訓練語言模型在解答應用問題上有很好的表現，協助進行定理證明以及其他數學任務。然而，將其用於數學推理卻存在若干挑戰。
首先，預訓練語言模型不是專門針對數學資料的訓練。這可能導致它們在數學相關任務中的熟練程度低於自然語言任務。與文字資料相比，可用於大規模預訓練的數學或科學資料也較少。
其次，預訓練模型的規模持續成長，使得為特定的下游任務從頭開始訓練整個模型的成本很高。
此外，下游任務可能會處理不同的輸入格式或模態，例如結構化表格或圖表。為了應對這些挑戰，研究者必須透過在下游任務上對預訓練模型進行微調或調整神經架構。
最後，儘管預先訓練的語言模型可以編碼大量的語言訊息，但僅從語言建模的目標來看，模型可能很難學習數字表示或高階推理技能。考慮到這一點，最近有研究調查了從基礎知識開始的課程對數學相關技能的注入。
數學的自監督學習
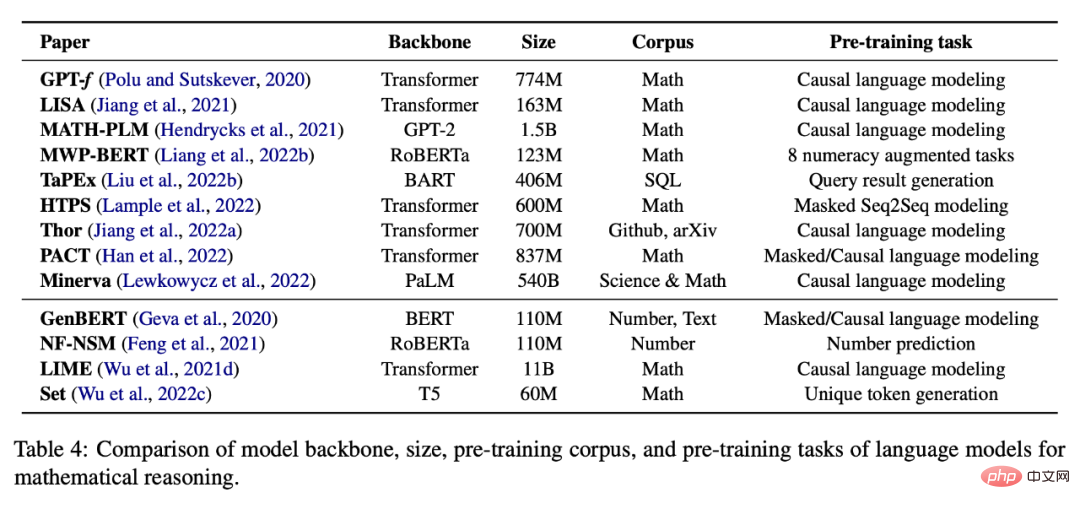
#下表4 提供了一個預先訓練了數學推理的自監督任務的語言模型列表。
特定任務的數學微調
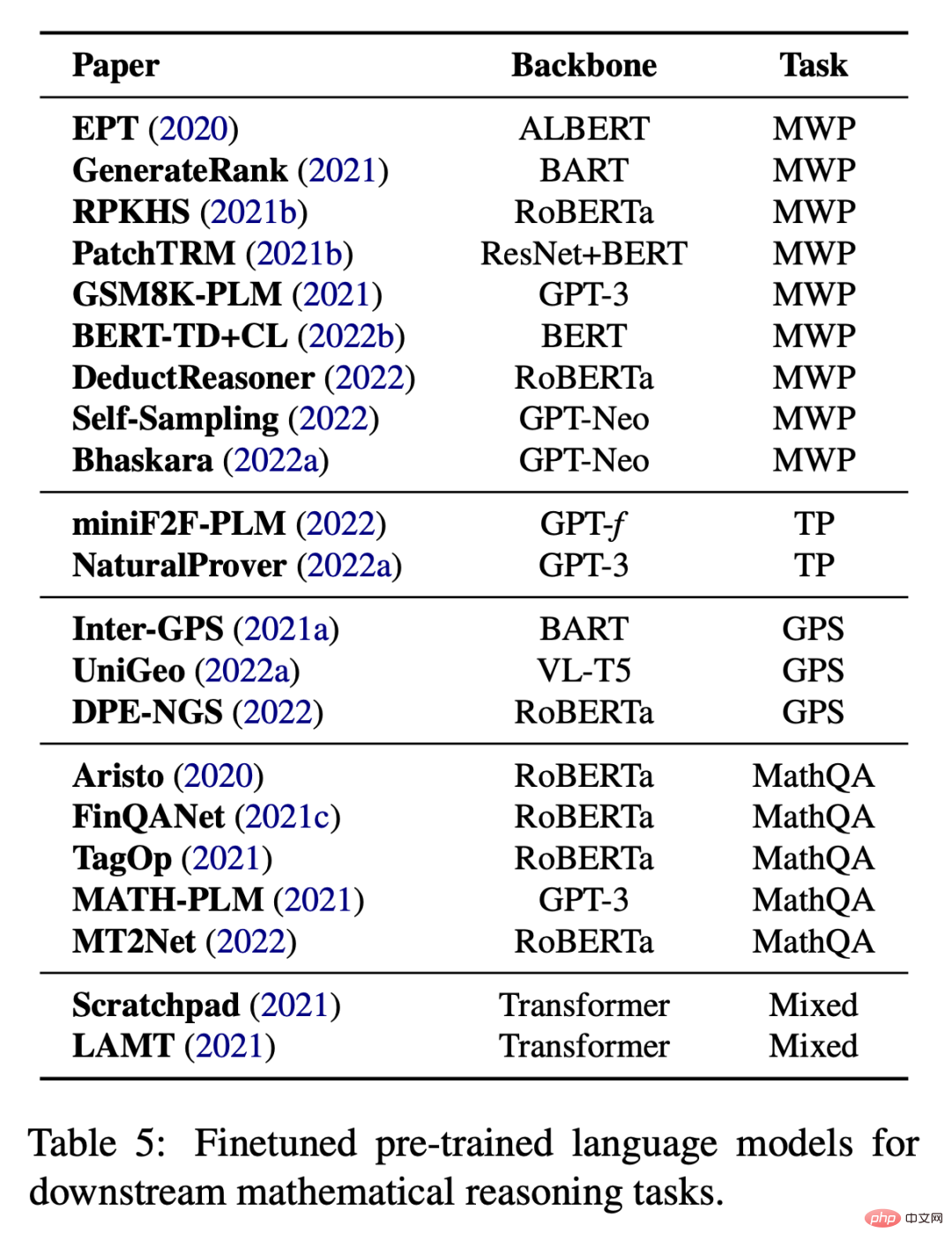
當沒有足夠的資料來從頭訓練大型模型時，特定任務的微調也是常見的做法。如表 5 所示，現有的工作嘗試了在各種下游任務上對預訓練語言模型進行微調。
In addition to fine-tuning model parameters, many works also use pre-trained language models as encoders and combine them with other modules to complete downstream tasks. For example, IconQA proposes to use ResNet and BERT for graph recognition and BERT respectively. Text comprehension.
A sample of context usually contains an input-output pair and some prompt words, for example, please select the largest number from the list .
Input: [2, 4, 1, 5, 8]
Output: 8.
Few-shot learning will give multiple samples, and then the model will predict the output on the last input sample. However, this standard few-shot prompting, which provides large language models with contextual samples of input-output pairs before test-time samples, has not been proven to be sufficient to achieve good performance on challenging tasks such as mathematical reasoning.
Chain-of-thought prompting (CoT) uses the intermediate natural language explanation as a prompt, allowing a large language model to first generate a reasoning chain and then predict the answer to an input question. For example, a CoT prompt for solving a word problem could be "Let's think step by step!" prompt will make large language models good zero-shot inferencers. Apart from this, most recent work has focused on how to improve thought chain reasoning in the setting of zero-shot inference. This type of work is mainly divided into two parts: (i) selecting better contextual samples and (ii) creating better inference chains.
Early thought chain work was to select context samples randomly or heuristically. Recent research has shown that this type of few-shot learning can be very unstable under different selections of contextual examples. Therefore, which contextual reasoning samples can make the most efficient prompts is still an unknown issue in academic circles. To address this limitation, some recent works have investigated various methods to optimize the context sample selection process. For example, Rubin et al. (2022) attempted to solve this problem by retrieving semantically similar samples. However, this approach does not work well on mathematical reasoning problems, and it is difficult to measure similarity if structured information (such as tables) is included. In addition, Fu et al. (2022) proposed a complexity-based prompt, selecting samples with complex reasoning chains (i.e., chains with more reasoning steps) as prompts. Lu et al. (2022b) proposed a method to select contextual samples through reinforcement learning. Specifically, the agent learns to find the best contextual sample from a pool of candidates, with the goal of maximizing the predicted reward for a given training sample when interacting with the GPT-3 environment. Furthermore, Zhang et al. (2022b) found that diversification of example problems can also improve model performance. They proposed a two-step approach to construct example problems in context: first, divide the problems of a given dataset into several groups; second, select a representative problem from each group and use A simple heuristic's zero-shot thinking chain generates its reasoning chain.
High quality reasoning chain
Early thought chain work mainly relied on a single human annotated reasoning chain as prompt . However, manually creating reasoning chains has two disadvantages: first, as tasks become more and more complex, current models may not be sufficient to learn to perform all necessary reasoning steps and cannot be easily generalized to different tasks; second, a single The decoding process is easily affected by faulty reasoning steps, leading to incorrect predictions in the final answer. To address this limitation, recent research has mainly focused on two aspects: (i) hand-crafting more complex examples, known as process-based methods; (ii) utilizing ensemble-like methods, known as outcome-based methods. After evaluating existing benchmarks and methods, the authors also discuss future research directions in this area. For more research details, please refer to the original paper.
以上是十年來論文量激增，深度學習如何慢慢推開數學推理的門的詳細內容。更多資訊請關注PHP中文網其他相關文章！
