神經網路在訓練時的最佳化首先是對模型的當前狀態進行誤差估計,然後為了減少下一次評估的誤差,需要使用一個能夠表示錯誤函數對權重進行更新,這個函數稱為損失函數。

損失函數的選擇與神經網路模型從範例中學習的特定預測建模問題(例如分類或回歸)有關。在本文中我們將介紹常用的一些損失函數,包括:
迴歸預測模型主要是用來預測連續的數值。所以我們將使用 scikit-learn的 make_regression() 函數來產生一些模擬數據,並使用這些數據來建立迴歸模型。
我們將產生 20 個輸入特徵:其中 10 個特徵將是有意義的,但 10 個與問題無關。
並且隨機產生 1,000 個範例。並且指定隨機種子,所以無論何時運行程式碼都會產生相同的 1,000 個範例。

將實值輸入和輸出變數縮放到合理的範圍通常可以提高神經網路的效能。所以我們要對資料進行標準化處理。
StandardScaler也可以在scikit-learn庫中找到,為了簡化問題我們將在將所有資料分割為訓練集和測試集之前對其進行縮放。

然後平均分割訓練和驗證集
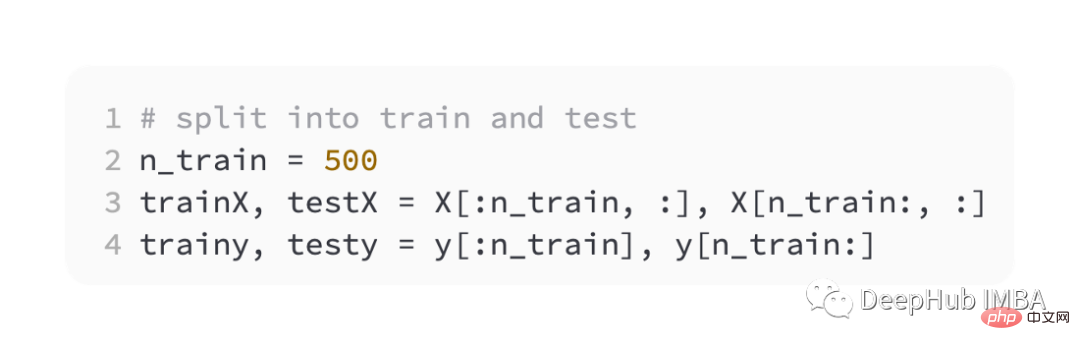
#為了介紹不同的損失函數,我們將開發一個小型多層感知器(MLP)模型。
根據問題定義,有20個特徵作為輸入,經過我們的模型。需要要預測的實值,所以輸出層會有一個節點。

我們使用SGD進行最佳化,並且學習率為0.01,動量為0.9,兩者都是合理的預設值。訓練將進行100個輪,測試集將在每個階段結束時進行評估,並且繪製學習曲線。

模型完成後就可以進行損失函數的介紹:
迴歸問題最常使用的是均方誤差損失(MSE)。當目標變數的分佈為高斯分佈時,它是最大似然推理下的首選損失函數。所以只有當你有一個更好的理由時,才應該改變為其他損失函數。
如果在 Keras 中編譯模型時將「mse」或「mean_squared_error」指定為損失函數,則使用均方誤差損失函數。

下面的程式碼是上述迴歸問題的完整範例。
在運行範例的第一步中,列印了模型的訓練和測試資料集的均方誤差,因為保留了3位小數,所以顯示為0.000

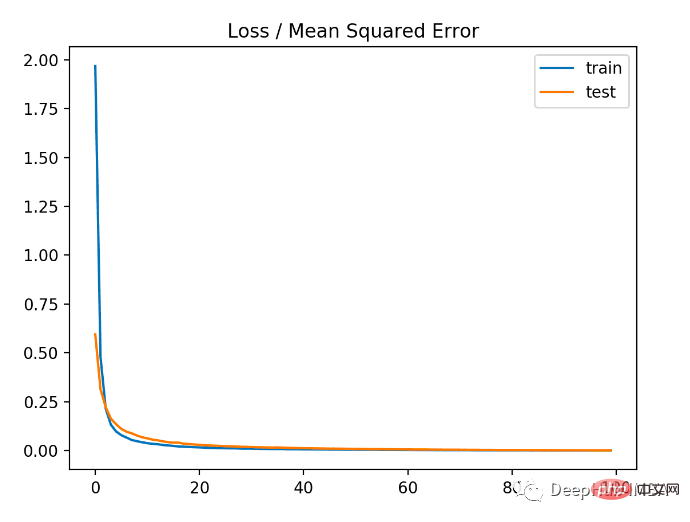
從下圖可以看出,模型收斂速度相當快,訓練和測試表現保持不變。根據模型的表現和收斂特性,均方誤差是迴歸問題的一個很好的選擇。
在具有廣泛值的迴歸問題中,可能不希望在預測大值時像均方誤差那樣對模型進行懲罰。所以可以先計算每個預測值的自然對數來計算均方誤差。這種損失稱為 MSLE,或均方對數誤差。
當預測值出現較大差異時,它具有放鬆懲罰效果的效果。當模型直接預測未縮放的數量時,它可能是更合適的損失測量。
keras中使用「mean_squared_logarithmic_error」作為損失函數

在下面的範例是使用MSLE損失函數的完整程式碼。

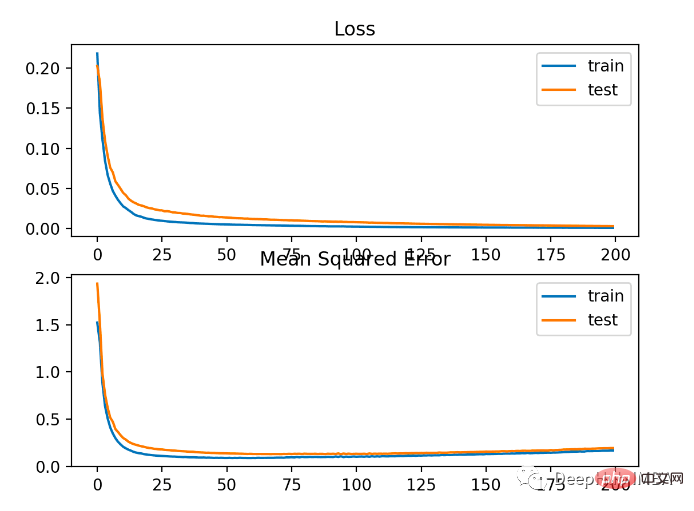
該模型在訓練和測試資料集上的MSE都略差。這是由於目標變數的分佈是一個標準的高斯分佈,說明我們的這個損失函數可能不是很適合這個問題。

下圖顯示各訓練輪次的比較MSE收斂得很好,但MSE可能過度擬合了,因為它從20輪開始下降變得變換並且開始上升。
根據迴歸問題,目標變數的分佈可能主要是高斯分佈,但可能包含異常值,例如遠離平均值的大值或小值。
在這種情況下,平均絕對誤差或 MAE 損失是一個合適的損失函數,因為它對異常值更穩健。考慮實際值與預測值的絕對差值,計算為平均值。
使用「mean_absolute_error」損失函數

#這是使用MAE的完整程式碼

如下

下圖可以看到,MAE確實收斂了但它有一個顛簸的過程。 MAE在這種情況下也不是很適合,因為目標變數是沒有大離群值的高斯函數。
二元分類問題是預測建模問題中兩個標籤中的一個。這個問題被定義為預測第一個或第二個類別的值為0或1,一般情況下通常被實現為預測屬於類別值1的機率。
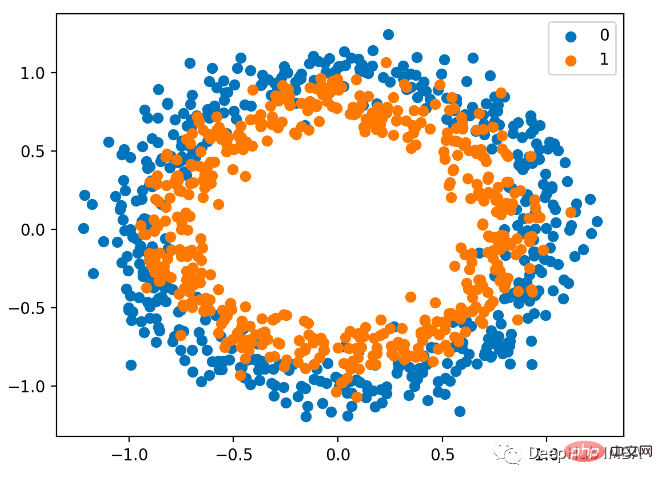
我們也是使用sklearn產生資料這裡使用圓問題,它有一個二維平面,有兩個同心圓,其中外圓上的點屬於類別0,內圓上的點屬於類別1。為了讓學習更具挑戰性,我們也在樣本中加入了統計雜訊。樣本量為1000,並加入10%的統計雜訊。

資料集的散佈圖可以幫助我們理解正在建模的問題。下面列出的是一個完整的範例。

散佈圖如下,其中輸入變數決定點的位置,顏色為類別值。 0是藍色的,1是橘色的。
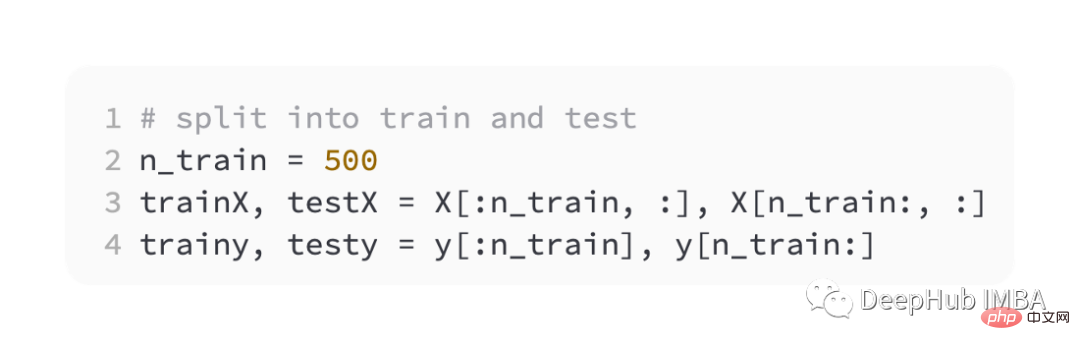
這裡還是一半用於訓練,一半用於測試,
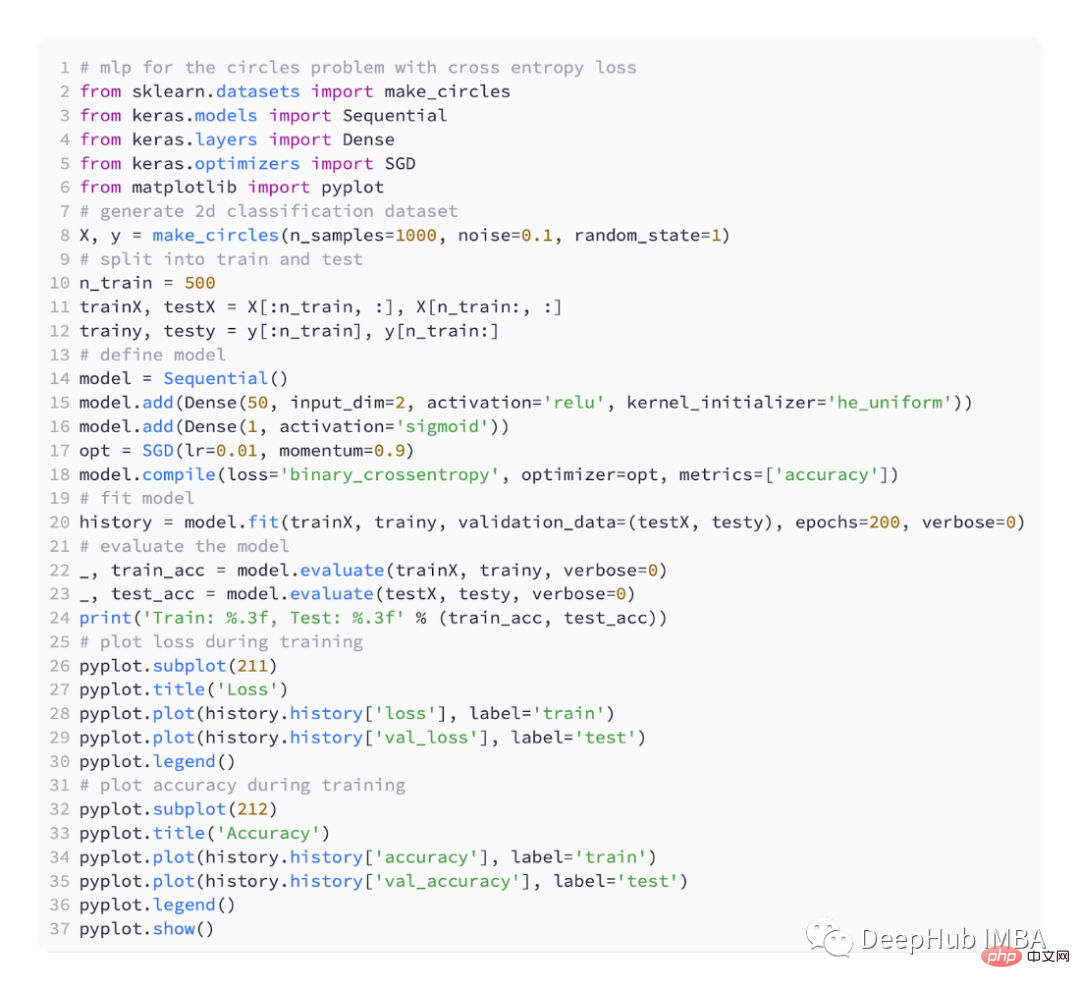
我們還是定義一個簡單的MLP模型,

使用SGD最佳化,學習率為0.01,動量為0.99。

模型訓練200輪進行擬合,並根據損失和準確性評估模型的性能。

BCE是用來解決的二元分類問題預設損失函數。在最大似然推理框架下,它是首選損失函數。對於第1類的預測,交叉熵計算一個分數,該分數總結了實際和預測機率分佈之間的平均差異。
在編譯Keras模型時,可以指定binary_crossentropy作為損失函數。

為了預測類別1的機率,輸出層必須包含一個節點和一個' sigmoid '啟動。

以下是完整的程式碼:
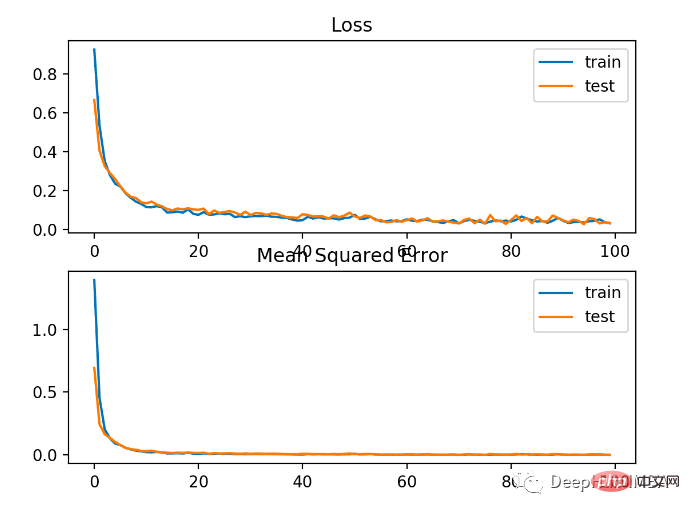
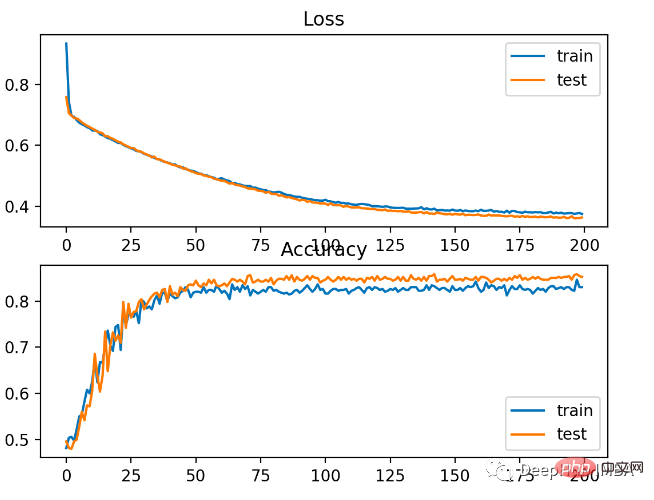
#該模型對問題的學習相對較好,在測試資料集上的準確率為83%,準確率為85%。分數之間存在一定程度的重疊,表示模型既不是過度擬合也不是欠擬合。
下圖所示,訓練效果很好。由於機率分佈之間的誤差是連續的,損失圖是平滑的,而精度線圖顯示出凹凸不平,因為訓練和測試集中的例子只能被預測為正確或不正確,提供的顆粒資訊較少。
支援向量機 (SVM) 模型使用Hinge 損失函數作為交叉熵的替代來解決二元分類問題。
目標值在是集合 [-1, 1] ,旨在與二進位分類一起使用。如果實際類別值和預測類別值的符號不同,則Hinge會得到更大的誤差。在二元分類問題上它有時比交叉熵更好。
作為第一步,我們必須將目標變數的值修改為集合 {-1, 1}。

keras中它被稱為' hinge '。

在網路的輸出層中,必須使用tanh激活函數的單一節點以輸出介於 -1 和 1 之間的單一值。

以下是完整程式碼:

#比交叉熵略差的效能,在訓練和測試集上的準確性不到80%。
下圖可以看出,模型已經收斂,分類精度圖顯示也已經收斂。
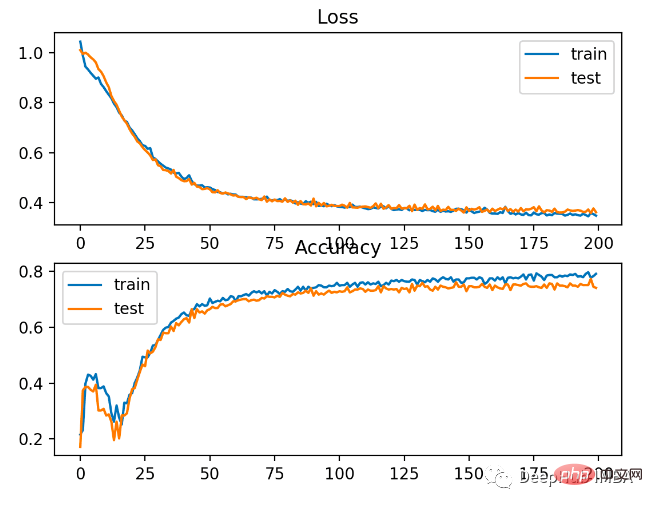
可以看到這個問題還是BCE比較好,這裡可能的原因就是因為我們有一些雜訊點導致的
以上是訓練深度學習神經網路的常用五個損失函數的詳細內容。更多資訊請關注PHP中文網其他相關文章!




