Java中二元樹的基礎知識及概念是什麼？

1. 樹型結構

1.1概念

樹是一種非線性的資料結構，它是由n （ n> ;=0 ）個有限結點組成一個有層次關係的集合。把它叫做樹是因為它看 起來像一棵倒掛的樹，也就是說它是根朝上，而葉朝下的 。

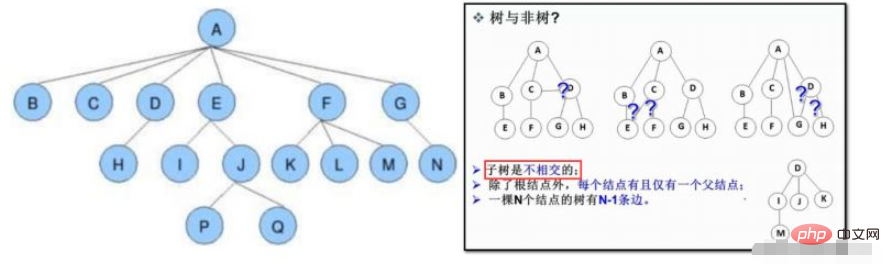
1.2 概念（重要）

a.節點的度數：此節點子樹的數目；如上圖：A的度數為6，J的度數為2

b.樹的度：在該樹中，最大結點的度為該數的度數；如上圖：樹的度數為6

c.葉節點（終端節點）：度為0的節點（沒有子樹的節點）

d.雙親結點/父節點：如上圖：D是H的父節點

孩子節點/子節點：如上圖：H是D的子節點

e.根節點：沒有雙親的節點；如上圖：A

f.節點的層次：從根開始定義起，根為第1層，根的子節點為第2層，以此類推；

g.樹的高度或深度：樹中節點的最大層次； 如上圖：樹的高度為4

2. 二元樹（重點）

2.1 概念

每個節點最多只有兩顆子樹，度

2.2 二元樹的基本形態

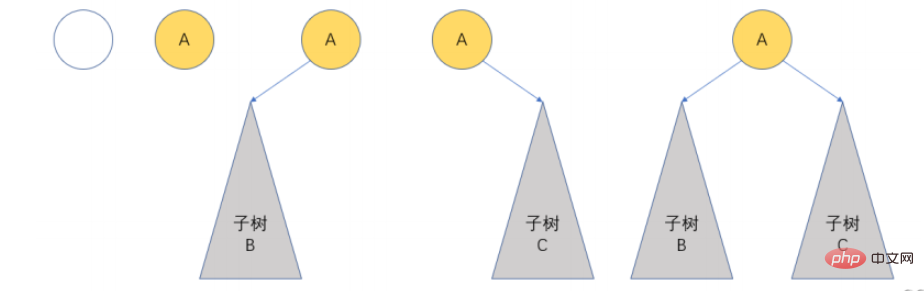
2.3 兩種特殊的二元樹

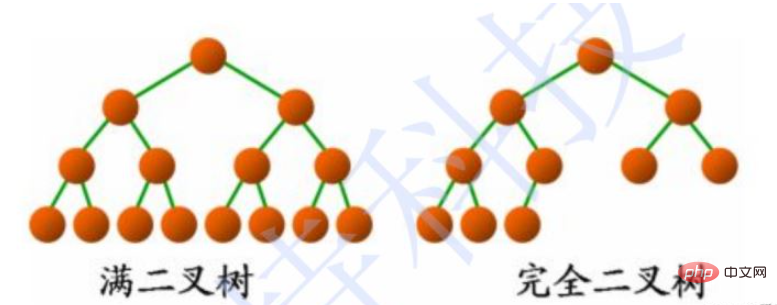
#a.滿二叉樹：非子葉度都為2

#b.完全二元樹：滿二叉樹缺了「右下角」

2.4 二元樹的性質

a.滿一個二元樹

1.高度為K，則有2^k-1個節點

2.層次為K，則該層有2^(k-1)個節點

3.邊數= 節點個數- 1

4.度為0有n0個，度為2有n2個，則n0 = n2 1

b.完全二元樹

#1.有右孩子必有左孩子

2.只可能有一個度為1的節點

2.5 二元樹的儲存

二元樹的儲存結構分為：順序存儲和類似鍊錶的鍊式存儲。

順序儲存：只能存完全二元樹

鍊式儲存：普通二元樹

本次展示鍊式儲存

二元樹的鍊式儲存是透過一個一個的節點引用起來的，常見的表示方式有二元和三叉表示方式，

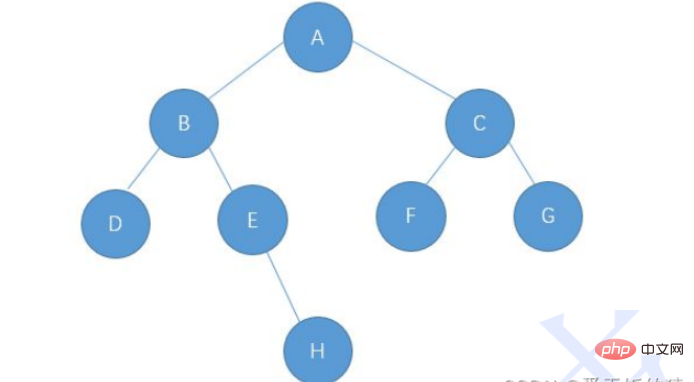
以此圖為例， 具體如下：

// 孩子表示法
private static class TreeNode{
    char val;
    TreeNode left;
    TreeNode right;
 
    public TreeNode(char val) {
        this.val = val;
    }
}

初始化：

    public static TreeNode build(){
        TreeNode nodeA=new TreeNode('A');
        TreeNode nodeB=new TreeNode('B');
        TreeNode nodeC=new TreeNode('C');
        TreeNode nodeD=new TreeNode('D');
        TreeNode nodeE=new TreeNode('E');
        TreeNode nodeF=new TreeNode('F');
        TreeNode nodeG=new TreeNode('G');
        TreeNode nodeH=new TreeNode('H');
        nodeA.left=nodeB;
        nodeA.right=nodeC;
        nodeB.left=nodeD;
        nodeB.right=nodeE;
        nodeE.right=nodeH;
        nodeC.left=nodeF;
        nodeC.right=nodeG;
        return nodeA;
    }

2.6 二元樹的基本操作

2.6.1 二元樹的遍歷(遞歸)

1. NLR ：前序遍歷(Preorder Traversal 亦稱先序遍歷)—— 訪問根結點---> 根的左子樹---> 根的右子樹。

    //先序遍历 : 根左右
    public static void preOrder(TreeNode root){
        if(root==null){
            return;
        }
        System.out.print(root.val+" ");
        preOrder(root.left);
        preOrder(root.right);
    }

2. LNR ：中序遍歷 (Inorder Traversal)—— 根的左子樹 ---> 根節點 ---> 根的右子樹。

    //中序遍历
    public static void inOrder(TreeNode root){
        if(root==null){
            return;
        }
        preOrder(root.left);
        System.out.print(root.val+" ");
        preOrder(root.right);
    }

3. LRN ：後序遍歷 (Postorder Traversal)—— 根的左子樹 ---> 根的右子樹 ---> 根節點。

    //后序遍历
    public static void postOrder(TreeNode root){
        if(root==null){
            return;
        }
        preOrder(root.left);
        preOrder(root.right);
        System.out.print(root.val+" ");
    }

2.6.2 二元樹的遍歷(迭代)

1.前序遍歷

    //方法2(迭代)
    //先序遍历 (迭代)
    public static void preOrderNonRecursion(TreeNode root){
        if(root==null){
            return ;
        }
        Deque<TreeNode> stack=new LinkedList<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode cur=stack.pop();
            System.out.print(cur.val+" ");
            if(cur.right!=null){
                stack.push(cur.right);
            }
            if(cur.left!=null){
                stack.push(cur.left);
            }
        }
    }

2.中序遍歷

    //方法2(迭代)
    //中序遍历 (迭代)
    public static void inorderTraversalNonRecursion(TreeNode root) {
        if(root==null){
            return ;
        }
 
        Deque<TreeNode> stack=new LinkedList<>();
        // 当前走到的节点
        TreeNode cur=root;
        while (!stack.isEmpty() || cur!=null){
            // 不管三七二十一，先一路向左走到根儿~
            while (cur!=null){
                stack.push(cur);
                cur=cur.left;
            }
            // 此时cur为空，说明走到了null，此时栈顶就存放了左树为空的节点
            cur=stack.pop();
            System.out.print(cur.val+" ");
            // 继续访问右子树
            cur=cur.right;
        }
    }

3.後序遍歷

    //方法2(迭代)
    //后序遍历 (迭代)
    public static void postOrderNonRecursion(TreeNode root){
        if(root==null){
            return;
        }
        Deque<TreeNode> stack=new LinkedList<>();
        TreeNode cur=root;
        TreeNode prev=null;
 
        while (!stack.isEmpty() || cur!=null){
            while (cur!=null){
                stack.push(cur);
                cur=cur.left;
            }
 
            cur=stack.pop();
            if(cur.right==null || prev==cur.right){
                System.out.print(cur.val+" ");
                prev=cur;
                cur=null;
            }else {
                stack.push(cur);
                cur=cur.right;
            }
        }
    }

2.6.3 二元樹的基本操作

1.求結點個數（遞歸&迭代）

    //方法1(递归)
    //传入一颗二叉树的根节点，就能统计出当前二叉树中一共有多少个节点，返回节点数
    //此时的访问就不再是输出节点值，而是计数器 + 1操作
    public static int getNodes(TreeNode root){
        if(root==null){
            return 0;
        }
        return 1+getNodes(root.left)+getNodes(root.right);
    }
 
    //方法2(迭代)
    //使用层序遍历来统计当前树中的节点个数
    public static int getNodesNoRecursion(TreeNode root){
        if(root==null){
            return 0;
        }
        int size=0;
        Deque<TreeNode> queue=new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            size++;
            if (cur.left != null) {
                queue.offer(cur.left);
            }
            if (cur.right != null) {
                queue.offer(cur.right);
            }
        }
        return size;
    }

2.求葉子結點個數（遞歸&迭代）

    //方法1(递归)
    //传入一颗二叉树的根节点，就能统计出当前二叉树的叶子结点个数
    public static int getLeafNodes(TreeNode root){
        if(root==null){
            return 0;
        }
        if(root.left==null && root.right==null){
            return 1;
        }
        return getLeafNodes(root.left)+getLeafNodes(root.right);
    }
 
    //方法2(迭代)
    //使用层序遍历来统计叶子结点的个数
    public static int getLeafNodesNoRecursion(TreeNode root){
        if(root==null){
            return 0;
        }
        int size=0;
        Deque<TreeNode> queue=new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()){
            TreeNode cur=queue.poll();
            if(cur.left==null && cur.right==null){
                size++;
            }
            if(cur.left!=null){
                queue.offer(cur.left);
            }
            if(cur.right!=null){
                queue.offer(cur.right);
            }
        }
        return size;
    }

3.求第k 層結點個數

    //求出以root为根节点的二叉树第k层的节点个数
    public static int getKLevelNodes(TreeNode root,int k){
        if(root==null || k<=0){
            return 0;
        }
        if(k==1){
            return 1;
        }
        return getKLevelNodes(root.left,k-1)+getKLevelNodes(root.right,k-1);
    }

4.求樹的高度

    //传入一个以root为根节点的二叉树，就能求出该树的高度
    public static int height(TreeNode root){
        if(root==null){
            return 0;
        }
        return 1+ Math.max(height(root.left),height(root.right));
    }

5.判斷二元樹數中是否存在值為value的節點

    //判断当前以root为根节点的二叉树中是否包含指定元素val，
    //若存在返回true，不存在返回false
    public static boolean contains(TreeNode root,char value){
        if(root==null){
            return false;
        }
        if(root.val==value){
            return true;
        }
        return contains(root.left,value) || contains(root.right,value);
    }

2.7 二元樹的層序遍歷

    //层序遍历
    public static void levelOrder(TreeNode root) {
        if(root==null){
            return ;
        }
 
        // 借助队列来实现遍历过程
        Deque<TreeNode> queue =new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()){
            int size=queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode cur=queue.poll();
                System.out.print(cur.val+" ");
                if(cur.left!=null){
                    queue.offer(cur.left);
                }
                if(cur.right!=null){
                    queue.offer(cur.right);
                }
            }
        }
    }

以上是Java中二元樹的基礎知識及概念是什麼？的詳細內容。更多資訊請關注PHP中文網其他相關文章！