首先我們補充說明一下什麼是二元搜尋樹:
在二元搜尋樹中,對於每一個節點來說,他的左子樹中的值都比他小,右子樹的中的值都比他大。所以二元搜尋樹的中序遍歷是一組有順序的資料。
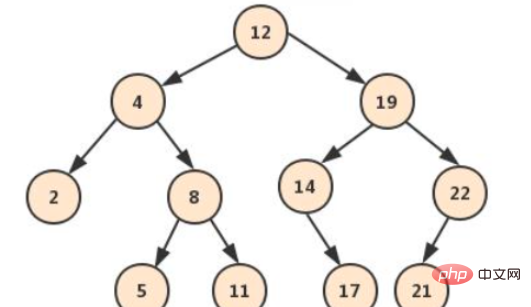
對於上述這棵樹,假設要求 p q 的最近公共祖先。
那麼它有以下情況:
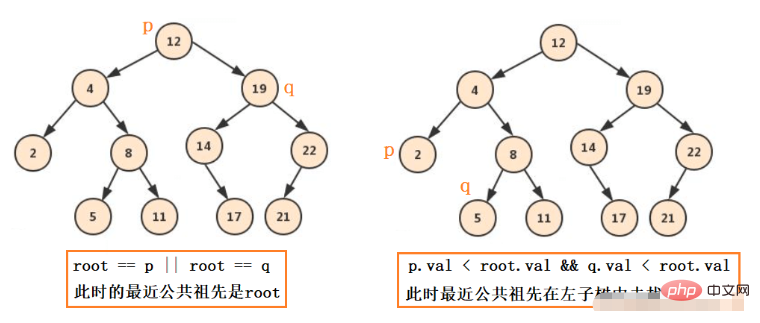
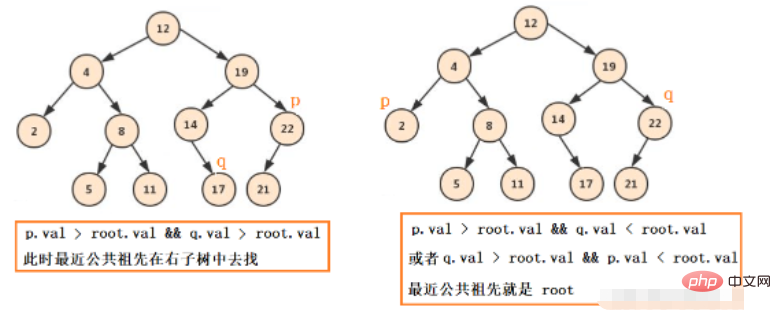
#對於普通的二元樹來說,也無非就這幾種情況:pq都在左,pq都在右,pq一左一右,pq有一個是根節點。
所以分別遞歸的去左子樹和右子樹中找 p q 節點的公共祖先,找到了則返回該節點,沒有找到則返回空。
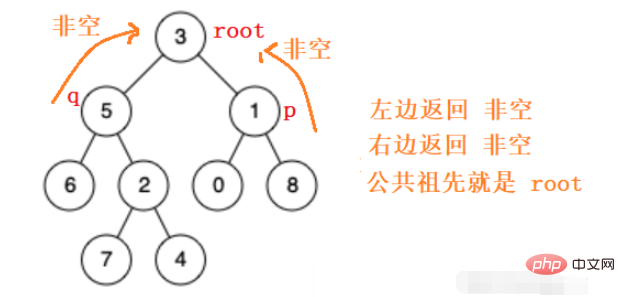
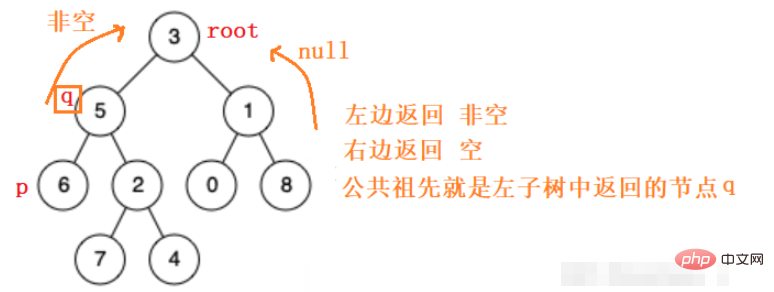
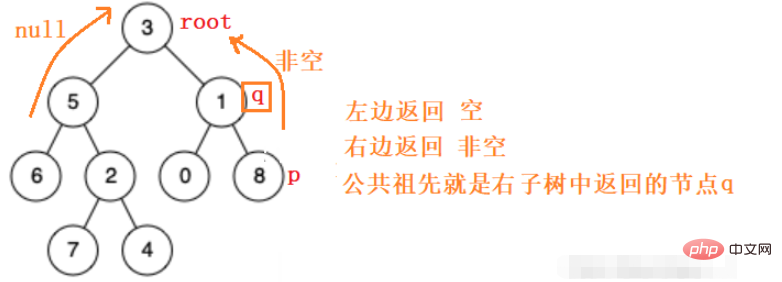
#根據上述思路,我們很容易寫出程式碼
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null) return null;
// p 为当前树的根节点
if(p == root) return p;
// q 为当前树的根节点
if(q == root) return q;
// 去左子树中找
TreeNode left = lowestCommonAncestor(root.left,p,q);
// 去右子树中找
TreeNode right = lowestCommonAncestor(root.right,p,q);
// 左边右边都找到了
if(left != null && right != null) {
return root;
}
// 左边找到了,右边没找到
if(left != null) {
return left;
}
if(right != null) {
return right;
}
return null;
}每個節點會保存它父親節點的位址,可以層層網上找,直到找到兩鍊錶的第一個交點,該交點就是他們的公共祖先。
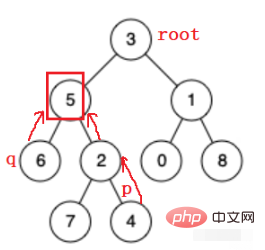
而對於普通的二元樹來說,只能層層往下找,不能往上,所以要保留兩個節點的路徑,直到兩路徑的最後一個相同節點。這裡我們用堆疊來保留兩個節點的路徑。
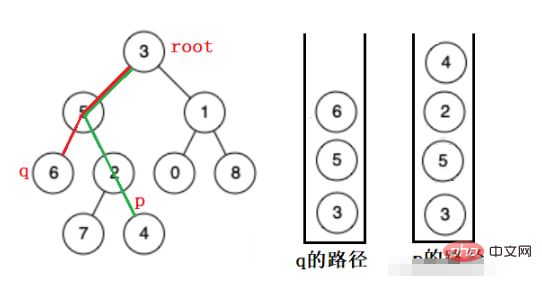
先彈出元素多的堆疊中的元素,然後兩個堆疊再一起彈出,直到要彈出的節點相等,就是其最近公共祖先。
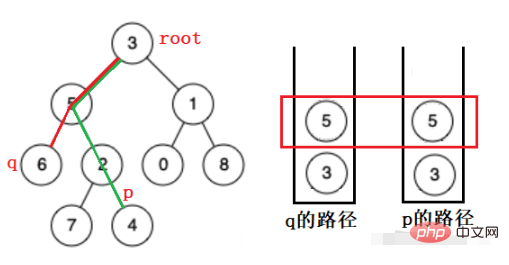
那麼這裡最大的困難就是儲存路徑。
這裡用堆疊來儲存路徑,當遍歷到一個節點時,將該節點放入堆疊中,再遞歸該節點的左樹和右樹找,如果找到了則保留路徑,沒找到則彈出。
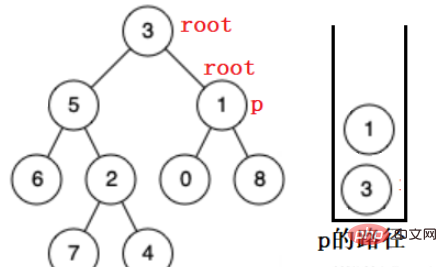
假設找下圖的p:
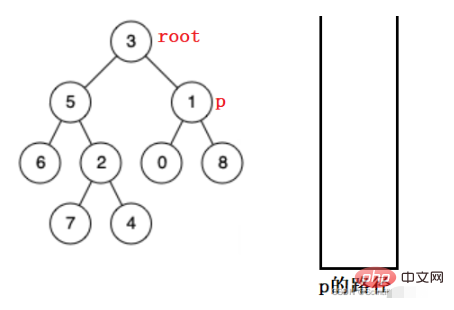
先將根節點放入棧,遞歸root節點的左子樹找,找不到則彈出,在右子樹找。
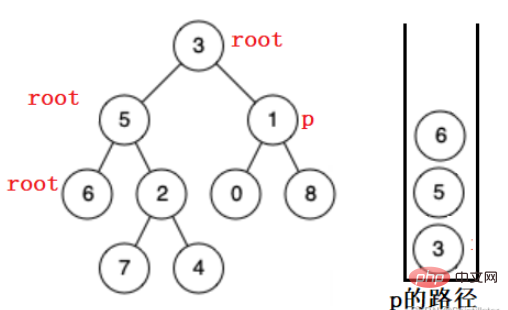
當root 走到6 的時候,發現該節點的左右均為空,說明在該子樹中沒找到目標節點,彈出6 ,在5 的右子樹中繼續找。
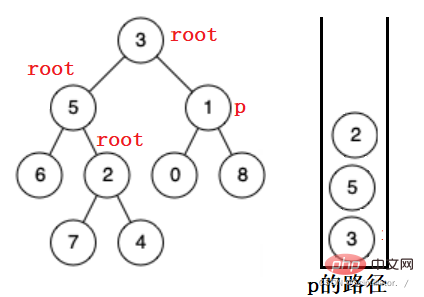
同理在 5 的右子樹中也找不到,會彈出直到去 3 的右子樹找,來到 1 ,找到。
// 用于找节点的路径
public boolean getPath(TreeNode root, TreeNode node, Stack<TreeNode> stack) {
if(root == null || node == null) {
return false;
}
// 将当前节点放入栈中
stack.push(root);
if(root.val == node.val) {
return true;// 找到了
}
// 当前节点没找到,去左子树找
boolean flag = getPath(root.left,node,stack);
// 左子树中找到了,直接返回
if(flag) {
return true;
}
// 左子树没找到,去右子树找
flag = getPath(root.right,node,stack);
// 右子树中找到了,直接返回
if(flag) {
return true;
}
// 左右子树都没找到,弹出节点
stack.pop();
return false;
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null) {
return null;
}
Stack<TreeNode> stackp = new Stack<>();
Stack<TreeNode> stackq = new Stack<>();
// 分别得到 p q 的路径
getPath(root,p,stackp);
getPath(root,q,stackq);
int sizep = stackp.size();
int sizeq = stackq.size();
if(sizep > sizeq) {
int size = sizep - sizeq;
// 弹出元素直至两栈中元素个数相等
while(size > 0) {
stackp.pop();
size--;
}
}else {
int size = sizeq - sizep;
// 弹出元素直至两栈中元素个数相等
while(size > 0) {
stackq.pop();
size--;
}
}
// 一起弹出,直到找到第一个相同的元素
while(!stackp.isEmpty() && !stackq.isEmpty()) {
if(stackp.peek() == stackq.peek()) {
// 找到了,就返回该节点
return stackq.pop();
}else {
stackp.pop();
stackq.pop();
}
}
// 没找到,返回 null
return null;
}以上是Java怎麼找二元樹的最近公共祖先的詳細內容。更多資訊請關注PHP中文網其他相關文章!




