圖機器學習無所不在，使用 Transformer 可緩解 GNN 限制

在我們今天的生活中，圖的示例包括社交網絡、例如Twitter、Mastodon、以及任何鏈接論文和作者的引文網絡，分子，知識圖、例如UML 圖、百科全書以及有超鏈接的網站，表示為句法樹的句子以及任何的3D 網格等，可以說圖表已經無所不在。

近日，Hugging Face 研究科學家 Clémentine Fourrier 在文章《Introduction to Graph Machine Learning》就介紹了今天這種無所不在的圖機器學習。什麼是圖形？為什麼要使用圖？如何最好地表示圖？人們如何在圖上學習？ Clémentine Fourrier 指出，圖是對由關係連結項目的描述，其中，從前神經方法到圖神經網路仍然是目前人們常用的圖上學習方法。

此外，研究人員近期也開始考慮將 Transformers 應用於圖中，Transformer 具有良好的可擴展性，可緩解 GNN 存在的部分限制，前景十分可觀。

1 圖是對關係連結項目的描述

#本質來看，圖是由關係連結項目的描述。圖（或網路）的項目稱為節點（或頂點），由邊（或連結）來進行連接。例如在社交網路中，節點是用戶，邊是用戶彼此間的連結；在分子中，節點是原子，邊緣是它們的分子鍵。

• 一個有類型節點或類型邊的圖稱為異質圖，舉個例子，在引文網絡的項目可以是論文或作者，有類型節點，而XML 圖中的關係有類型邊；它不能僅僅透過其拓撲結構來表示，還需要額外的資訊
• 圖也可以是有向的（例如追蹤者網絡， A 跟隨B 並不表示B 跟隨A）或無向的（例如分子、原子之間的關係是雙向的）。邊可以連接不同的節點或一個節點與自身（自邊），但並非所有節點都需要連接

可以看到，使用資料必須先考慮其最佳表示，包括同質/異質、有向/無向等。

在圖層面，主要任務包括以下：

• #圖形生成，用於藥物發現以生成新的合理分子
• 圖演化，即給定一個圖來預測它將如何隨時間演化，在物理學中可用於預測系統的演化
• 圖層預測，來自圖的分類或迴歸任務，例如預測分子的毒性

#節點層通常是對節點屬性的預測，例如Alphafold 使用節點屬性預測來預測給定分子整體圖的原子3D 座標，從而預測分子如何在3D 空間中折疊，這是一個困難的生物化學問題。

邊緣的預測包括邊緣屬性預測和缺失邊緣預測。邊緣屬性預測有助於對藥物副作用的預測，給定一對藥物的不良副作用；缺失邊預測在推薦系統中則是用於預測圖中的兩個節點是否相關。

在子圖層級中，可進行社群偵測或子圖屬性預測。社交網路可透過社區檢測來確定人們的聯繫方式。子圖屬性預測多應用在行程系統中，例如Google地圖，可用於預測預計到達時間。

當要進行預測特定圖的演進時，轉換設定工作中的所有內容，包括訓練、驗證和測試等，都可在同一個圖上完成。但從單一圖表建立訓練、評估或是測試的資料集並非易事，許多工作會使用不同的圖（單獨的訓練/評估/測試拆分）完成，稱為歸納設定。

表示圖處理和操作的常見方法有兩種，一種是作為其所有邊的集合（可能由其所有節點的集合補充），或作為其所有節點之間的鄰接矩陣。其中，鄰接矩陣是方陣（節點大小×節點大小），指示哪些節點直接連接到其他節點。要注意的是，由於大多數圖並不是密集連接的，因此具有稀疏的鄰接矩陣會使計算更加困難。

圖與ML 中使用的典型物件非常不同，由於其拓撲結構比「序列」（如文字和音訊）或「有序網格」（如圖像和視訊）更複雜：即便可以將其表示為列表或矩陣，但這種表示不可以被視為是有序物件。也即是說，如果打亂一個句子中的單詞，就可以創造一個新句子，如果將一個圖像打亂並重新排列它的列，就能創建了一個新圖像。

圖註：Hugging Face 標誌和被打亂的Hugging Face 標誌，是完全不同的新形象

#但圖的情況並非如此：如果我們洗掉圖的邊緣列表或鄰接矩陣的列，它仍然是同一個圖。

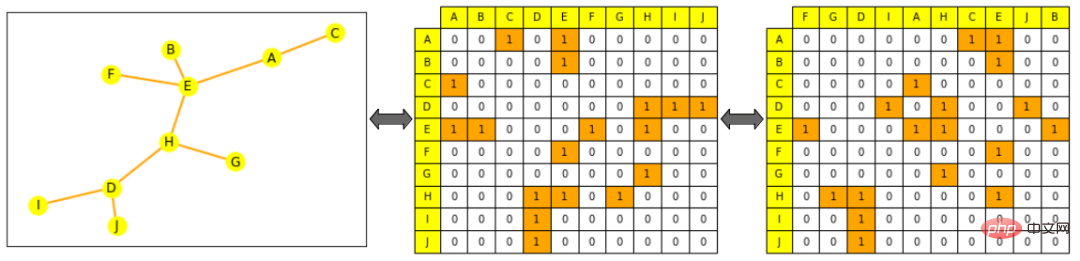
圖註：左邊是一個小圖，黃色表示節點，橘色表示邊；中心圖片上的鄰接矩陣，列和行按節點字母順序排列：節點A 的行（第一行）可以看到其連接到E 和C；右邊圖片打亂鄰接矩陣（列不再按字母順序排序），其仍為圖形的有效表示，即A 仍連接到E 和C

2 透過ML 的圖形表示

使用機器學習處理圖的常規過程，是首先為專案產生有意義的表示，其中，節點、邊或完整圖取決於特定任務需求，為目標任務訓練預測器。與其他模式一樣，可以透過限制物件的數學表示，以便在數學上與相似物件接近。但在此之中，相似性在圖 ML 中很難嚴格定義：例如，當兩個節點具有相同的標籤或相同的鄰居時，它們是否更相似？

如下面所示，本篇文章重點關注的是生成節點表示，一旦有了節點級的表示，就有可能獲得邊或圖級的資訊。對邊級訊息，可以將節點對的連接起來，或者做點乘；在圖級資訊中，可以對所有節點級表示的串聯張量進行全局池化，包括平均、求和等。但是，它仍然會使整個圖的資訊變得平滑和丟失——遞歸的分層集合可能更有意義，或者增加一個虛擬節點，與圖中的所有其他節點相連，並將其表示為整個圖的表示。

前神經方法

簡單地使用工程特性

##在神經網路之前，圖形及其感興趣的項目可以透過特定任務的方式表示為特徵的組合。在今天，這些特徵仍用於資料增強和半監督學習，儘管存在更複雜的特徵生成方法，但根據任務找到如何最好地將這些特徵提供給網路至關重要。

節點級特徵可以提供關於重要性的資訊以及基於結構的信息，並對其進行組合。

節點中心性可用來衡量圖中節點的重要性，透過對每個節點鄰居中心性求和直到收斂來遞歸計算，或透過節點間的最短距離度量來遞歸計算，節點度是其擁有的直接鄰居的數量；聚類係數衡量節點鄰居的連接程度；Graphlets 度向量計算則可計算有多少不同的graphlets 以給定節點為根，其中，graphlets 可使用給定數量的連接節點來建立的所有迷你圖。

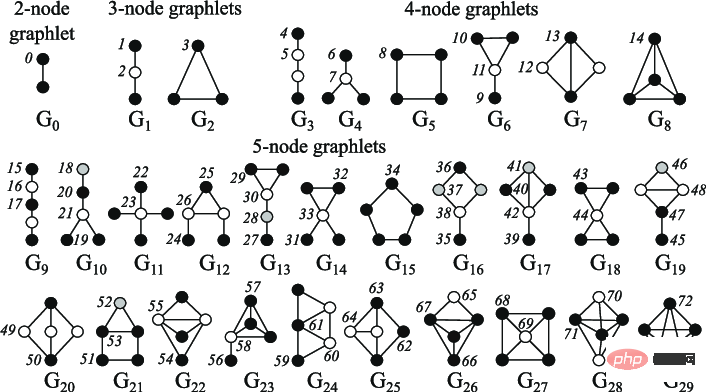
圖示：2 到5 節點小圖

#########邊級特徵以關於節點連通性的更詳細資訊補充表示，其中就包括了兩個節點之間的最短距離、它們的共同相鄰點以及Katz 指數（指兩個節點之間可能走過的一定長度的路徑的數量－其可以直接從鄰接矩陣中計算出來）。 ######

圖級特徵包含關於圖相似性和特殊性的高級信息，其中，小圖計數，儘管計算成本很高，但提供了關於子圖形狀的信息。核心方法透過不同的 "節點袋 "方法（類似詞袋）來衡量圖之間的相似性。

基於行走的方法

基於行走的方法使用隨機行走中從節點i 存取節點j 的機率來定義相似性度量，這些方法結合了局部和全局資訊。例如，先前 Node2Vec 模擬圖形節點之間的隨機遊走，使用 skip-gram 處理這些遊走，就像我們處理句子中的單字一樣，以計算嵌入。

這些方法也可用於加速PageRank 方法的計算，該方法給每個節點分配一個重要性分數，基於它與其他節點的連接，例如透過隨機行走來評估其訪問頻率。但上述方法也存在一定的局限性，它們不能獲得新節點的嵌入，不能很好地捕捉節點之間的結構相似性，不能使用添加的特徵。

3 圖神經網路如何處理圖表？

神經網路可以泛化到看不見的資料。考慮到先前提到的表示約束，一個好的神經網路應該如何處理圖？

下面展示了兩種方法：

• #是置換不變的：

• 方程式：f（P（G））=f（G）f（P（G））=f（G） ，其中f 是網絡，P 是置換函數，G 是圖
• 解釋：經過網路後，圖的表示及其排列應該相同

• 是置換等變的

• 方程式：P（f（G））=f（P（G））P（f（G））=f（P（G）），其中f 是網絡， P 是置換函數，G 是圖

• 解釋：在將節點傳遞到網路之前置換節點應該等同於置換它們的表示

典型的神經網路不是排列不變的，例如RNN 或CNN，因此一種新的架構－圖神經網路被引入（最初是作為一種基於狀態的機器）。

一個 GNN 是由連續的層組成的。 GNN 層將節點表示為其鄰居的表示和來自上一層（訊息傳遞）的自身組合 ，通常還會加上激活以添加一些非線性。而與其他模型相比，CNN 可視為具​​有固定鄰居大小（透過滑動視窗）和排序（非排列等變）的 GNN；而沒有位置嵌入的 Transformer 可以看作是全連接輸入圖上的 GNN。

聚合和訊息傳遞

聚合來自節點鄰居的資訊有很多方法，例如求和、平均，先前已有的類似聚類別方法包括：

• Graph Convolutional Networks，將節點鄰居的歸一化表示平均；
• ##Graph Attention Networks，學習根據它們的重要性來權衡不同鄰居（如Transformer）；
• GraphSAGE，在使用最大集合在幾個步驟中聚合資訊之前，在不同的躍點對鄰居進行採樣；
• Graph Isomorphism Networks，透過將MLP 應用於節點鄰居表示的總和來聚合表示。

選擇一個聚合：一些聚合技術（特別是平均/最大集合）在創建精細表示以區分類似節點的不同節點鄰居表示時，會遇到失敗的情況；例如，透過平均值集合，一個有4個節點鄰居表示為1、1、-1、-1，平均為0，與一個只有3個節點表示為-1、0、1的鄰居是沒有區別的。

GNN 形狀和過度平滑問題

在每個新層，節點表示包括越來越多的節點。一個節點經過第一層，是其直接鄰居的聚合。透過第二層，它仍然是其直接鄰居的聚合，但此刻其表示也包括了它們自己的鄰居（來自第一層）。在 n 層之後，所有節點的表示成為其距離為 n 的所有鄰居的集合，因此，如果其直徑小於n，則為全圖的聚合。

如果網路層數太多，則存在每個節點成為完整圖的聚合的風險（並且節點表示對所有節點收斂到相同的表示），這被稱為過度平滑問題，可透過以下方式來解決：

• 將GNN 縮放到足夠小的層數，因此不會將每個節點近似為整個網路（透過先分析圖的直徑和形狀）
• 增加層的複雜性
• #新增非訊息傳遞層來處理訊息（例如簡單的MLP）
• 新增跳過連接

過度平滑問題是圖ML 中的一個重要研究領域，由於它會阻止GNN 擴大規模，就像Transformers 在其他模型中被證明的那樣。

圖Transformers

沒有位置編碼層的Transformer 是置換不變的，而Transformer 還具有良好的可擴展性，因此研究人員在近期開始考慮將Transformers 應用在圖中。大多數方法的重點是透過尋找最佳特徵和最佳方式來表示圖形，並改變注意力以適應這種新數據。

下面展示了一些方法，這些方法在史丹佛大學的Open Graph Benchmark 上取得最先進或接近的結果：

• Graph Transformer for Graph-to-Sequence Learning，引入一個圖Transformer，它將節點表示為它們的嵌入和位置嵌入的串聯，節點關係表示二者間的最短路徑，並將兩者組合成一個關係——增強自我關注。
• Rethinking Graph Transformers with Spectral Attention，引入了Spectral Attention Networks （SAN），這些將節點特徵與學習的位置編碼（從拉普拉斯特徵向量/值計算）結合起來，用作注意力中的鍵和查詢，注意力值是邊緣特徵。
• GRPE: Relative Positional Encoding for Graph Transformer，介紹了圖相對位置編碼Transformer，其透過將圖級位置編碼與節點資訊、邊級位置編碼與節點資訊結合，並將兩者結合在註意力中來表示圖。
• Global Self-Attention as a Replacement for Graph Convolution ，引入了 Edge Augmented Transformer，該體系結構分別嵌入節點和邊緣，並將它們聚合在經過修改的注意力中。
• Do Transformers Really Perform Badly for Graph Representation，介紹了微軟的 Graphormer，它在 OGB 上問世時獲得了第一名。該架構使用節點特徵作為注意力中的查詢/鍵/值，並在註意力機制中將它們的表示與中心性、空間和邊緣編碼相結合。

近期有研究「Pure Transformers are Powerful Graph Learners」在方法中引入了TokenGT，將輸入圖表示為一系列節點和邊嵌入，也即使用正交節點標識符和可訓練類型標識符進行增強，沒有位置嵌入，並將此序列作為輸入提供給Transformers，此方法非常簡單，同時也非常有效。

#論文網址：https://arxiv.org/pdf/2207.02505.pdf

此外，在研究「Recipe for a General, Powerful, Scalable Graph Transformer」中，跟其他方法不同的是，它引入的不是模型而是框架，稱為GraphGPS，可允許將訊息傳遞網路與線性（遠端）Transformer 結合起來，輕鬆建立混合網路。該框架還包含幾個用於計算位置和結構編碼（節點、圖形、邊緣級別）、特徵增強、隨機遊走等的工具。

論文網址：https://arxiv.org/abs/2205.12454

Transformer 使用於圖在很大程度上仍處於起步階段，但就目前來看，其前景也十分可觀，它可以緩解GNN 的一些限制，例如縮放到更大或更密集的圖，或是在不過度平滑的情況下增加模型大小。

以上是圖機器學習無所不在，使用 Transformer 可緩解 GNN 限制的詳細內容。更多資訊請關注PHP中文網其他相關文章！