因果推論在微視激勵和供需場景的應用

一、因果推論與激勵演算法
#1、業務背景與業務建模
首先簡單介紹一下騰訊微視的紅包激勵業務背景。與其他的產品和場景類似,在給定的預算之下,我們向騰訊微視的用戶發放一些現金激勵,希望透過現金激勵最大化用戶的隔日留存和當天使用時長。現金激勵的形式主要是以不定的時間間隔為用戶發放不定數量和不定金額的現金紅包。以上提到的 3 個「不定」最終由演算法來決定。這三個「不定」也稱紅包激勵策略的三要素。
接下來講不同的現金激勵策略的抽象形式。第一種以紅包序列的形式來表示策略,例如將紅包序列編號,然後用 one-hot 的形式為每個 treatment 獨立編號。它的優點是能夠刻畫更多細節,例如每個紅包之間的金額等細緻的策略,以及相對應的效果。但這必然會需要更多的變數來表示策略,策略的探索空間非常大,另外在進行策略的探索和擇優時,也會需要更多的計算量。而第二種形式,也就是使用三要素的向量來表示策略,其形式更靈活,探索的效率也會更高,但是它確實會忽略了一些細節。第三種方式比較數學一點,即紅包序列直接變成一個關於時間 t 的函數,函數裡的參數可以構成向量,從而表示策略。因果問題的建模和策略的表示,極大程度地決定了因果效應估計的準確性和效率。
假設我們有了一個好的策略抽象和向量表示之後,接下來要做的就是選擇演算法框架。這裡有三種框架。 第一種框架在業界較為成熟,即使用因果推論結合多目標限制優化的方式來做策略的分配與最佳化。在這種框架中,因果推論主要負責的是估計不同策略對應的使用者核心指標,也就是我們所說的使用者次日留存和時長的收益提升。估計之後,我們利用多目標的約束最佳化來做離線的預算策略分配以滿足預算限制。 第二種就是離線強化學習結合多目標限制最佳化方法。這個方法我個人認為是比較有前景的,主要原因有兩個。第一個原因是在實際應用場景當中,策略非常多,強化學習本身是可以有效率地進行策略空間探索的,同時,由於我們的策略是有依賴的,而強化學習可以建模策略間的依賴;第二個原因是因為離線強化學本質其實就是一個反事實估計(contrafactual estimation)的問題,本身就具有強烈的因果屬性。然而遺憾的是,在我們的場景當中曾經嘗試離線強化學習的方法,但它在線上效果沒有達到理想的效果。究其原因,一方面是我們的方法問題,另一方面主要受限於數據。要訓練一個好的離線強化學習模型,需要資料中的策略分佈夠廣,或叫策略分佈的夠均勻。也就是說,我們使用的隨機數據也好,或者是觀測數據也好,希望能夠盡可能地探索到更多的這種策略,並且分佈的相對來說會均勻一些,這樣才能夠減少做反事實估計的變異數。最後一種演算法框架在廣告場景當中比較成熟,我們透過線上強化學習方式做流量控制和預算控制。這種方法的優點是可以及時、快速地回應線上的突發事件,同時對於預算的控制相對更準確。在引入因果之後,我們做流量選擇或控制的指標就不再是 ECPM 指標了,可能就是我們現在估計的次留和時長的一個提升量。經過我們一系列的實踐嘗試,最終選擇了第一種演算法框架,也就是因果推論結合多目標約束優化,原因是它更穩定且更可控,同時它對線上工程的依賴也更少。
#第一種演算法框架的 Pipeline 如下圖所示。首先離線計算使用者特徵,再用因果模型去預估使用者在不同策略下核心指標的提升量,也就是所謂的 uplift。基於預估的提升量,我們利用多目標最佳化來求解,從而分配最優策略。為了加速整個過程的計算,我們在結構化時,會提前對人群進行聚類,也就是說我們認為這一簇裡邊的人具有相同的因果,相應的,我們給同一簇人分配同樣的策略。

2、策略假設與因果圖
#基於上述討論,接下來將重點討論怎麼做策略的抽象。首先來看我們如何抽象因果圖。在紅包激勵場景中需要建模的因果,體現在多天與多個紅包之間。因為前一個紅包肯定會影響下一個紅包是否要領取,因此它本質上就是一個 Time-Varying Treatment Effect 問題,抽象成時序因果圖由如右圖所示。
以一天內多個紅包為例,T 所有下標都代表的是紅包的一個序號。此時的 T 代表的是目前紅包的金額,以及距離上一個紅包發放的時間間隔所組成的向量。 Y 是用戶的紅包下發之後的當次使用時長,和次日留存的提升量。 X 是截止到當下時刻觀察到的混淆變量,例如使用者的觀看行為或人口屬性等。當然還會有很多未觀測的混淆變量,用 U 來表示,例如用戶偶發的停留,或是偶發的停止領。一個重要的未觀測混淆變數是使用者的心智,主要包括使用者對紅包激勵的金額的價值評估。而這些所謂的心智,是很難透過系統內的一些統計量或統計特徵來表示的。
如果以時間序列的形式去做建模紅包策略會非常複雜,因此我們做了一些合理的簡化。例如假設 U 只影響當下時刻的 T,X 和 Y,並且它只影響下一時刻的 U,也就是使用者心智。也就是說它只會透過影響下一刻的價值評估或心智來影響未來的 Y。但即使做了一系列簡化,我們也會發現整個時序因果圖依然很稠密,很難做合理的估計。並且當使用 G-methods 的方法解決 time Varying Trend Effect 時,需要大量資料去訓練,然而現實中我們得到的資料非常稀疏,所以很難在線上取得一個很好的效果。因此最後我們做了大量簡化,得到右下圖這樣的叉狀結構(Fork)。我們把所有當天的紅包的策略做了一個聚合,它是由策略三要素(紅包激勵總金額、總時間、總個數)所構成的向量,用 T 來表示。 X 是 T-1 時刻的混淆變量,也就截止到當天之前使用者的歷史行為和人口屬性。 Y 代表的是當天使用者的使用時長,就是使用者的次日留存或當次使用時長指標。雖然這種方法看起來忽略了許多細節,例如紅包之間的相互影響。但從宏觀的角度來說,這個策略更穩定也能更好衡量其效果。

3、策略表示與因果模型
基於上面討論,接下來就是核心問題,也就是如何表示策略(treatment)。之前我們嘗試了使用 One-Hot 對三要素向量獨立編號,以及將三要素分開,用時間函數建構 multi-variable treatment。前面這兩種策略表示方法比較好理解,接下來介紹最後一種方法。大家看上面這張圖。我們分別建構了三要素關於 t 的正弦函數,也就是給定一個時刻 T,我們可以分別得到金額、時間間隔和個數。我們用這些函數對應的參數作為新向量的元素,類似策略三要素的表示。我們用函數的方式來表示策略的目的是期望保留更多的細節,因為前兩種方法只能透過策略組合知道紅包金額、發放間隔的平均值,而用函數可能表示得更細緻。但是這種方式有可能引入更多的變量,使計算更加複雜。
#有了策略表示之後,就可以針對性地去選擇因果模型來去估計因果效應。在以 One-Hot 表示 T 的三要素的形式下,我們採用 x-Learner 的模型對每個策略建模,並將總金額最小的策略作為基準策略,從而計算和評估所有策略的 treatment effect。在這種情況下,大家可能感覺到它的效率是非常低的,而且模型缺乏泛化性。因此我們進一步採用剛才提到的第三種策略表示,即用正弦函數要素的向量去構成一個 treatment。接下來用單一 DML 模型來估計所有策略相對於基準策略的效果。此外,我們也做了一個最佳化 DML,假設 y 是混淆變數和因果效應的線性加權,也就是 y 等於 treatment effect 加上混淆變數。這樣就人工構造了向量要素之間的交叉項與高階項。相當於構造了 polynomial kernel function 來引入非線性函數。在這個基礎上 DML 相對於基準策略有了很大的提升。由右下圖的分析可以發現,DML 模型花了更少的錢並且提高了 ROI,這意味著我們能夠更有效率地去利用資源。
前面我們主要討論了一些方法上的抽象和模型的選擇,在實踐過程當中,還會發現一些比較偏業務方面的問題,比如做One-Hot 時treatment 怎麼辦?這時候,我們做了一個逐批擴充的策略。首先透過策略三要素做種子策略,然後人工篩選和保留優質的種子之後,對它進行一個擴展。在擴展之後,我們會基於一段時間,例如先在上線的前兩週分批地上線新的策略,並且保證每個策略的隨機流量大小是一致的,或是可比的。在這個過程當中,確實會忽略時間因素的影響,並且不斷替換效果較差的策略,從而把策略的集合豐富起來。另外,由於時間因素一定會影響隨機流量的策略是否可比較。因此我們建構了類似時間片輪轉的方法,確保其涵蓋的時間片是一致的,從而消除時間因素對策略的影響,這樣得到的隨機流量就可以用來訓練模型了。
還有就是新的策略大概要如何產生?一個簡單的方法是用 grade search,或是做遺傳演算法,這些是比較常見的搜尋的通用演算法。另外我們可以結合了人工剪枝,例如剪去一些不可取的紅包序列類型。還有一種方法是使用 BanditNet,也就是一種離線強化學習的方法去計算沒見過的策略,即估計反事實(counterfactual)的效果的估計,然後用估計的值來做策略的選擇。當然我們最後也需要用線上隨機流量去驗證的,原因是這種離線強化學習的方法,其方差大機率會非常的大。

4、策略問題與迭代
除了上述提到的問題,我們也會遇到一些偏業務的問題。第一個問題是使用者策略的更新周期是怎麼樣的?是不是所有的使用者策略都是頻繁更新會更好?對此,我們實踐的經驗是因人而異。例如高頻用戶的策略變化應該會更緩慢一些。一方面是因為高頻用戶已經很熟悉我們的形態了,包括激勵金額,如果紅包金額劇烈的變化,一定會影響相應的指標。所以我們對高頻用戶其實是保持一個週更新的策略,一週更新一次;但是對於新用戶來講,更新周期是更短的。原因是我們對新用戶了解很少,我們希望能夠更快速地去探索合適的策略,並且根據用戶互動情況快速回應做出策略變化。由於新用戶的行為也很稀疏,所以在這種情況下,我們就會用天級別對新用戶或一些低頻用戶去做更新。另外,我們也需要對策略的穩定性做監控,以避免特徵雜訊造成的影響,我們搭建的 Pipeline 如右圖所示。這裡我們會監控 treatment effect 是否穩定,同時也會對用戶最終分配的策略進行天級別的監控,例如今天的策略和昨天策略差異有多大,包括金額和個數。我們也會對線上的策略定期的做快照,主要是為了去做 debug,同時也能夠快速回放,從而確保策略的穩定。另外我們也會對小流量做實驗,監控其穩定性,只有達到穩定性要求的小流量實驗,才會被用來取代現成的策略。
第二個問題是針對新使用者以及某些特殊使用者的策略是否為獨立的?答案是確定的,例如新用戶,我們會先對他進行一個較強的激勵,而後激勵強度隨時間衰減。當使用者進入正常的生命週期之後,我們才會對他進行常規的激勵策略。同時,對於特殊的敏感人群,他們金額上會有限制策略,對此我們也會訓練獨立的模型去適應這類人群。
第三個問題大家可能會問到,也就是因果推論在整個演算法框架當中到底有多重要?從理論角度,我們認為因果推論是核心,因為它在激勵演算法中是帶來很大的利益。相對於迴歸與分類模型來說,因果推論與業務目標一致,它天生就是 ROI 導向的,所以它會帶來關於提升量的最佳化目標。但要提醒大家的是,我們在做預算分配的時候,不能夠為每個使用者都選擇最優的策略,而且因果效應相對於個人來說是相對較小的。當我們做預算分配的時候,很有可能會把一些使用者因果效應的差異消除了。在這種時候,我們約束優化會大幅影響策略效果。因此,在做聚類的時候,我們也嘗試了更多的聚類方法,例如深度聚類 SCCL 方法獲得了更好的聚類結果。我們也進行了一些深度因果模型的迭代,例如像 BNN 或 Dragonnet 等等。
我們發現在實踐的過程中,深度因果模型的離線指標確實有不錯的提升,但是其在線上的效果還不夠穩定,主要的原因是有缺失值的出現。同時我們也發現,特徵的規劃方法很影響深度學習線上模型的穩定性,所以最終我們還是會傾向於穩定的去使用 DML 方法。
在激勵場景的分享就這麼多,接下來也請我們團隊的另外兩位同學和大家分享一下在供需調優場景的一些實踐和理論的探索。

二、因果推論與供需調節
1、業務背景與業務建模
接下來介紹一下騰訊微視在供需方面的一個業務背景。作為一個短視頻平台,微視有許多個不同品類的影片。對於有時候不同觀看興趣的使用者群體,我們需要根據不同的使用者特徵去適當地分配各個品類的曝光佔比或者是庫存佔比,目標則是為了提升使用者的體驗和使用者的觀看時長,其中使用者的體驗可以根據3 秒快劃率指標來進行衡量,觀看時間長度主要以總的播放時間長度來去衡量。如何去調節影片品類的曝光佔比或庫存佔比?我們主要考慮的方式按比例去對一些品類進行增加或減少。 增減的比例是一個預設的數值。
接下來我們需要透過演算法解決如何決定哪些品類增,哪些品類減,去使得使用者體驗和觀看時長可以最大化,同時還需要滿足例如總曝光有限制的一些約束條件。這個地方總結了三個主要的建模思路。 第一個是比較直接的想法,就是我們直接把增和減作為一個0 和1 的treatment 變量,我們去估計它的因果效應,隨後再進行一個多目標的約束優化,去得到一個最終的策略。 第二種思路就對 treatment 建模得更精細一些。我們把 treatment 當作一個連續的變量,例如品類的曝光佔比,就是一個 0 到 1 之間連續變化的變數。然後去擬合一個對應的因果效應的曲線或因果效應函數,接下來再進行多目標的限制優化,最後得到最終的策略。可以注意到,剛剛提到的兩種方法都是兩階段的方法。 第三種思路,我們將約束條件帶入因果效應的估計當中,從而得到一個滿足約束條件的最優策略。這也是稍後希望和大家分享的研究內容。
首先還是先關注前兩種建模的思路,有幾個建模的要點要注意一下。第一個點是,為了確保因果效應估計的準確性,我們需要劃分人群,在每個人群上做二值 Treatment 或是連續 Treatment 的因果效應估計。剛剛鄭老師也有提過度人群的方法,例如用 Kmeans 聚類,或是一些深度聚類。第二點則是如何在非隨機實驗數據上評估模型效果。例如我們需要在不做 AB test 的情況下,離線評估模型的效果。關於這個問題,可以參考 PPT 上面索引的這篇論文中提到的一些指標,用來做離線的評估。第三點要注意的是,我們應該盡可能考慮品類之間的關聯和相互影響,例如相似品類之間的一些擠佔的問題等等。如果能把這些因素納入因果效應的估計當中,應該可以得到更好的效果。

2、單一群體× 類別曝光佔比調節策略
接下來我們就具體展開這幾種建模思路。首先第一種建模方式就是定義一個0 和1 的treatment,用來代表增加或減少這兩種介入的手段,可以參考左側的簡要因果圖,這裡x 代表使用者的一些特徵,例如歷史操作行為相關的統計特徵,以及其他的使用者屬性等等。 y 就是我們所關心的目標,也就是 3 秒快化率或播放總時長。除此之外,還需要注意的是一些未觀測的混淆變量,例如用戶的偶發、快滑和退出,以及同一個用戶可能實際上會有多個人在使用,這也是用戶多重身份的一個問題。另外就是推薦策略的不斷迭代和更新也會對觀測資料構成影響,還有另外使用者興趣的遷移也是觀測之外的。這些未觀測的混淆變量,可能會對因果效應的估計造成一定程度上的影響。
#對於這樣的建模方式,常見的因果效應估計方法都可以解決。例如可以考慮 T-Learner 或是 X-Learner,或是 DML,這些都可以進行因果效應估計。當然,這種簡單的建模方式也存在一些問題,例如我們用二值 treatment 進行建模會太過於簡化。另外,在這種方式之下,每一個品類是單獨考慮的,沒有考慮品類之間的相關性。最後一個問題就是我們整個問題裡邊沒有考慮到曝光的順序,以及內容的品質這些具體的因素。
接下來再介紹第二種建模的想法。我們把所有品類放在一起考慮,例如我們有 k 個視訊品類,令 treatment 是一個 k 維的原因向量。向量的每一個位置代表一個品類,例如影視綜藝或 MOBA 賽事等,0 和 1 仍然是代表增加或減少。這時候多維向量的 treatment 的因果效應估計可以透過 DML 演算法來解決。我們通常是把全為 0 的 treatment 向量當作 control。這種方式雖然解決了各品類沒有被單獨考慮的問題,但是它依然存在一些潛在的問題。首先是品類過多時所帶來的維度爆炸的問題,並且隨著維度的增加,由於每個位置上都有0 和1 兩種情況,所以潛在的排列組合數量會指數級增加,這些都會對因果效應估計的準確度造成乾擾。另外,前面所提到的曝光順序和內容等等這些因素也沒有考慮到。

#分享完二值變數treatment 的建模思路之後,接下來可以對treatment進行更精細,也更符合其本身特徵的建模。我們注意到,曝光佔比本身是一個連續的變量,因此我們用連續的 treatment 去進行建模會更加的合理。在這種建模思路之下,我們首先還是需要劃分人群。對每個人群,我們對每個品類進行單獨建模,得到一個單人群*單品類的因果效應曲線。就像左圖顯示的這樣,因果效應曲線代表的是不同品類比比對我們所關心的目標所產生的影響。為了估計這樣的因果效應曲線,我主要分享兩個可行的演算法,一個是 DR-Net,一個是 VC-Net,這兩種演算法都屬於深度學習的範疇。模型的結構就像右圖展示的。
先介紹 DR-Net。模型的輸入 x 首先會經過幾個全連接層,從而得到一個隱含的表示,叫做 z。 DR-Net 採取了離散化的策略,它將連續的 treatment 離散成多個 block,然後每個 block 分別訓練一個子網路來進行目標變數的預測。由於 DR-Net 採用了離散化的策略,所以它最終得到的因果效應曲線並不是嚴格連續的,但隨著離散化的分段越細,最終的估計會越接近連續的曲線。當然,隨著理想化的分段越細,由此帶來的就是更多的參數量以及更高的過度擬合的風險。
#接下來再分享一下 VC-Net。 VC-Net 一定程度上改進了 DR-Net 的缺點。首先 VC-Net 模型的輸入還是 X,也是使用者的特徵。它首先也是經過幾個全連接層之後得到一個隱含的表示 Z。但在 Z 這個地方,首先會接著一個預測 Propensity Score 的一個模組。在連續的 Treatment 條件下, Propensity 是給定 X 條件下 Treatment t 的一個機率密度,也是圖上所表示的 π。接下來我們來看Z 之後的網路結構,有別於DR-Net 進行離散化的操作,VC-Net 採用的是變係數的網路結構,也就是Z 之後的每一個模型參數,都是一個關於t的函數。我們這裡提到的文獻作者採用了基底函數的手段,把每個函數表示成一個基底函數的線性組合,也就這寫的 θ(t)。這樣一來,函數的估計也變成了對基底函數線性組合的參數估計。所以這樣一來,模型的參數最佳化就不成問題了,同時VC-Net 所得到的因果效應曲線也是一條連續的曲線。關於 VC-Net 要求解的目標函數由幾個部分組成。一方面,它是由最後對目標的預測的平方損失構成,也就是圖中的 μ。另一方面,它也由 propensity 的機率密度的對數損失來構成。除了這兩部分之外,作者在目標函數裡邊還加入了一個叫做 targeted regularization 的懲罰項,由此可以得到雙重穩健的估計性質。具體細節,有興趣的朋友可以參考上面索引的 2 篇原論文,去獲得更多的細節。

#最後,即將與大家分享的一篇我們的研究做個鋪墊。我們注意到,各個視訊品類的曝光佔比是一個多維連續的向量。它之所以多維,是在於我們有多個視訊品類,每個維度代表一個視訊品類。它之所以是連續的,主要就在於每個視訊品類的曝光佔比都是連續的,其取值都在 0 和 1 之間。同時還有一個很自然的限制條件,就是我們所有的視訊品類的曝光佔比加起來一定是等於 1。所以我們可以考慮這樣一個多維連續的向量去作為 treatment。
右圖所展示的向量就是這樣的例子。我們的目標是找到最優的曝光佔比,使得我們總播放時間最大化。在傳統的因果框架上,演算法很難解決這樣一個多維連續且待約束的問題。接下來分享我們對這樣的問題所做的研究。

三、帶有約束的連續多變量因果模型分享
#MDPP Forest 這項工作是團隊在研究供需問題的時候做的一個方法探索和問題的創新解決。我們團隊當時發現,在面對如何解決為每個使用者去分配最佳的視訊類別曝光比的問題上,其他現有的常用方法都沒有辦法得到一個比較符合預期的結果。因此經過一段時間的嘗試與改進,我們團隊設計的方法能在離線上取得了不錯的效果,然後與推薦合作,最後也取得了一定的策略效益。隨後我們把這項工作整理成了論文,也有幸發表在了 KDD 2022 上。

1、背景與挑戰
## 1、背景與挑戰###############首先介紹問題背景。在供需問題中,我們將短片依內容分為不同類目,例如科普、影視、戶外美食等。影片類目曝光比即指這些不同類目的影片各自所佔一位使用者觀看的所有影片的比例。使用者對不同類目的偏好有很大的差別,平台也往往需要因人而異地去決定每個類目的最優曝光比例。在重新排序階段,對各類影片的推薦加以控制。該公司面臨的一大挑戰是如何分配最佳的視訊曝光比,從而最大限度地延長每個用戶在平台上的使用時長。 ##########

這樣一個問題的主要困難在於以下的三點。第一個就是短影片的推薦系統中,每個使用者看到的影片和他自身的特徵會有非常強的相關關係,這就是一個存在的選擇性偏差。因此我們需要用因果推論相關的演算法來消除偏差。第二個是視訊類目曝光比是一種連續、多維且帶有約束的 treatment。這樣的複雜問題在因果推論和策略最佳化領域目前是沒有非常成熟的方法的。第三是在離線資料上,我們並不能先驗地知道每個人的真實最優曝光比,因此很難去評估這個方法。在真實環境下,它只是推薦中的一個子環節。最終實驗結果也無法判斷這個方法對它本身的計算目標的準確度。因此,這個場景的問題我們很難去準確地評估它。我們會在後續介紹我們是如何進行效果評估的。

2、問題定義
我們先把數據抽象化成一個統計學中的因果圖。其中X 是使用者特徵,包含了許多同時影響當前影片曝光以及使用者時長的混淆變數;T 是視訊類目曝光比,它也是treatment,在這個問題中具有比較高的維度,例如它是一個20 維的向量。 Y 是使用者的觀看時長,也就是任務目標的回應。我們建模的目標就是在特定的使用者特徵 X 下,給予一個高維度的最優視訊類目曝光比,從而使用戶的觀看時長期望達到最大。這個問題看似可以簡單地用一個因果三元圖來表示它,但有一個很大的問題,也就是前面提到的,我們的treatment 是多個類目的曝光比,它是由品類曝光佔比建構的多維連續取值且向量和為1 的向量。這樣的問題就比較複雜了。

3、方法簡介— Maximum Difference Point of Preference (MDP2) Forest
#對此,我們的方法也是基於因果決策森林(causal forest)的。一般的因果決策樹只能解決具有一維離散值的 treatment 問題。而我們透過改進中間分裂準則函數的計算,在分裂的時候增加一些高維連續的信息,使它可以解決高維連續值並且帶約束 treatment 的問題。

① 方法簡介-連續問題
首先,我們解決的是連續treatment 問題。如圖所示,T 對 Y 的影響是一條連續的曲線。我們先假設這是一條單調遞增的曲線。對於資料中所有的 Treatment 取值,我們去遍歷它,計算左右樣本的 Y 均值,從而找到左邊 Y 均值和右邊 Y 均值差異最大的點,也就是平均因果效益最大的點。我們把這個點稱為 Maximum Difference Point,也就是連續 Treatment 空間上效率最高的點,代表了 Treatment 能夠顯著地讓 Y 改變。 Maximum Difference Point 是我們在單一維度上想去得到的點。
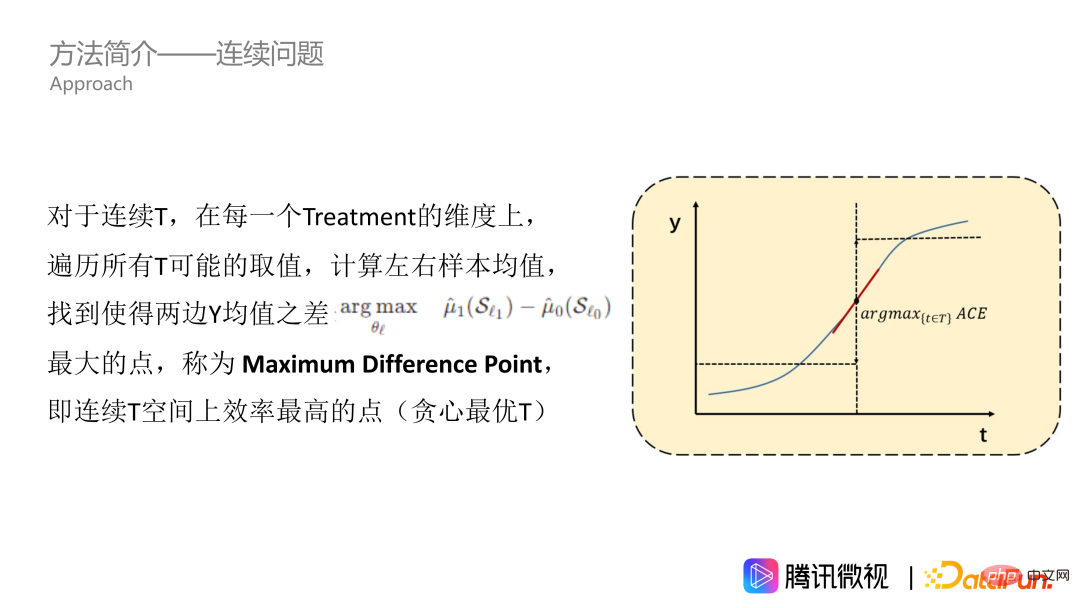
然而,我們剛才提到的方法只適用於單調遞增的曲線。但事實上,大部分問題都沒有那麼美好,特別是曝光比的問題。在這個問題上,效應曲線一般來說是山形的,即先增後減。因為多推薦用戶喜愛的視頻,可以使得用戶增加觀看時長,但是這個類型推得過多了,整個視頻的推薦就會變得非常單調乏味,並且還會擠佔其他用戶喜歡的視頻類型的曝光空間。所以曲線一般來說是山形的,也有可能是其他形狀的。為了適應任意形狀的T 曲線,我們需要進行積分的操作,也就是找值域區間進行累加。在累加後的曲線上,我們同樣計算左右兩邊均值,以及兩邊均值之差最大的點,比如圖裡的五角星。這個點就可以稱我們為 maximum difference point of preference,也就是我們的 MDPP。

② 方法簡介—高維度問題
上面我們介紹瞭如何解決連續問題,而剛才所說的曲線只是一維的,對應單一的視頻類目。接下來我們採用啟發式維度遍歷的想法去解決多維的問題。在計算分類分數的時候,我們採用啟發式的思想,將 K 個維度隨機排序,在每個維度上去計算一個 D 指標的聚合,也就是進行求和的操作。得到 D* 作為一個高維度資訊熵,再來考慮約束,約束是所有的 MDPP 總和為1。這裡我們要考慮下面兩種情況,一種是如果 K 維度遍歷完以後,它 MDPP 總和也沒有達到 1。針對這個情況,我們會把所有的 MDPP 總和加起來對它們做歸一化,拉到 1。第二個情況是,如果我們只遍歷了 K’ 維小於 K 維,但MDPP 總和就已經達到 1。對此,我們將停止遍歷,並且把 MDPP 設定為剩餘的“資源量”,即 1 減之前已經算出來 MDPP 值之和,這樣就可以去考慮到約束。

#另外,我們也會在上述的樹結構上引入forest,因為它主要有兩大意義。第一個是我們傳統的 bagging 整合思想,它可以用多個學習器增強模型的穩健性。第二個是在維度遍歷中,每次節點分裂只會計算到 K’ 個維度,有些維度沒有被算進去。為了使每個維度都能以平等的機會參與分裂中,我們需要建立多棵樹。

③ 方法簡介-演算法加速
另外還有一個問題,由於演算法包含了三層的遍歷,所有樹模型都需要特徵值的遍歷,還有額外引入的維度遍歷以及搜尋MDPP 的遍歷。這樣的三層遍歷使得效率非常低。因此我們對特徵值的遍歷和 MDPP 遍歷用了加權分位數圖的方法,只在分位數點去計算對應的結果,這樣就可以大幅降低演算法複雜度。同時,我們也找到了這些分位點作為「累加值域」的邊界點,這樣可以大幅減少計算量和儲存量。假設有q 個分位點,我們只需要計算q 次得出每段分位區間內的樣本數和y 的均值,這樣每次計算兩邊均值之差d 的時候,只需要把q 值分成左邊和右邊兩部分,分別把每一個區間裡的均值做一個加權求和就可以了。我們不需要再重新計算分位點左右兩邊所有樣本的平均數。我們下面進入實驗部分。

4、實驗設計
① 實驗設計-Metric
我們實驗評估本質上就是一個策略評估問題,因此我們引入了策略評估相關的指標。第一個是 Main Regret,它用於衡量整體策略的收益和理論最優收益之間的差距。另一個是 Main Treatment Square Error,用於衡量多維 Treatment 下每個 Treatment 維度的預估值和最優值之間的差距。這兩個指標都是越小越好的。然而,定下這兩個評估指標帶來的最大問題就是我們怎麼去決定最優值。

② 實驗設計-對比方法
② 實驗設計-對比方法

③ 實驗設計-模擬資料集


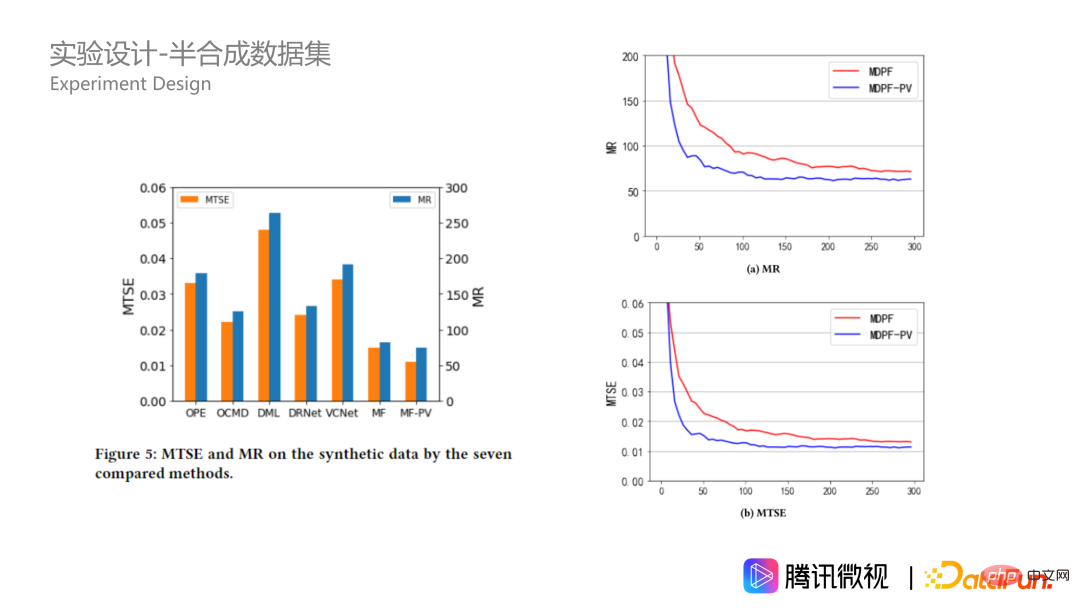
④ 實驗設計-半合成資料集
#除了模擬資料集之外,我們也根據真實的業務資料建構了一個半合成資料。數據來自騰訊微視平台。 Xi 表示使用者的 20 維特徵,treatment ti 表示多維的視訊類別曝光比構成了10 維向量, yi(ti)表示第 i 個使用者的使用長度。實際場景的一個特點是,我們並不能知道使用者真實的最優視訊曝光比。所以我們根據聚類中心規則去建構函數,產生虛擬的 y 來取代真實的 y,這使得樣本的 y 有更好的規律性。這裡具體公式我就不再贅述了,有興趣的同學可以看原文。為什麼可以這樣做呢?因為我們演算法的關鍵是它要能夠解決 x 和 t 之間的一些混雜的影響,也就是線上使用者受到有偏策略的影響。為了去評估策略的效果,我們只保留了 x 和 t 而改變了 y,以便更好地對問題進行評估。

#在半合成資料上,我們的演算法效果也明顯更好,而且比模擬資料集上的優勢會更加的大。由此說明了在數據複雜的情況下,我們 MDPP forests 演算法是更加的穩定的。另外,我們在合成資料來看超參數,也就是森林的規模。在右下圖我們可以看到,隨著森林規模的增加,兩種分裂準則處理下指標收斂的都比較好,帶懲罰項的一個始終會更好一些,它在100 棵樹的時候達到比較好的效果,250 棵樹的時候達到最優效果,再之後會有一些過擬合。
四、問答環節
Q:為什麼遍歷曝光度超過1 的時候,歸一化是可以work 的?
A:我的理解是這樣,因為我們做的是一個曝光佔比約束的最佳化,在這個過程當中,我們是一個相對值。我們在遍歷的過程當中,是尋找最優的一個分裂點,找出應該優先給哪個品類曝光較多的比例。在這個過程當中,我們只要能保證它是等比縮放的,就是可以的。
我也是同樣觀點,是等比縮放就可以。因為 1 是一個強的約束限制,我們一開始算出來的肯定不完全為 1,會低一些或高一些。如果多了很多,沒有辦法去讓它達到強約束唯一的條件,也是比較自然地用到一個歸一化的思考。因為我們考慮到各個類目之間相對大小關係。我覺得相對大小關係是比較重要的,而不是絕對值的問題。
#以上是因果推論在微視激勵和供需場景的應用的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 CLIP-BEVFormer:明確監督BEVFormer結構,提升長尾偵測性能
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer:明確監督BEVFormer結構,提升長尾偵測性能
Mar 26, 2024 pm 12:41 PM
寫在前面&筆者的個人理解目前,在整個自動駕駛系統當中,感知模組扮演了其中至關重要的角色,行駛在道路上的自動駕駛車輛只有通過感知模組獲得到準確的感知結果後,才能讓自動駕駛系統中的下游規控模組做出及時、正確的判斷和行為決策。目前,具備自動駕駛功能的汽車中通常會配備包括環視相機感測器、光達感測器以及毫米波雷達感測器在內的多種數據資訊感測器來收集不同模態的信息,用於實現準確的感知任務。基於純視覺的BEV感知演算法因其較低的硬體成本和易於部署的特點,以及其輸出結果能便捷地應用於各種下游任務,因此受到工業
 使用C++實現機器學習演算法:常見挑戰及解決方案
Jun 03, 2024 pm 01:25 PM
使用C++實現機器學習演算法:常見挑戰及解決方案
Jun 03, 2024 pm 01:25 PM
C++中機器學習演算法面臨的常見挑戰包括記憶體管理、多執行緒、效能最佳化和可維護性。解決方案包括使用智慧指標、現代線程庫、SIMD指令和第三方庫,並遵循程式碼風格指南和使用自動化工具。實作案例展示如何利用Eigen函式庫實現線性迴歸演算法,有效地管理記憶體和使用高效能矩陣操作。
 探究C++sort函數的底層原理與演算法選擇
Apr 02, 2024 pm 05:36 PM
探究C++sort函數的底層原理與演算法選擇
Apr 02, 2024 pm 05:36 PM
C++sort函數底層採用歸併排序,其複雜度為O(nlogn),並提供不同的排序演算法選擇,包括快速排序、堆排序和穩定排序。
 人工智慧可以預測犯罪嗎?探索CrimeGPT的能力
Mar 22, 2024 pm 10:10 PM
人工智慧可以預測犯罪嗎?探索CrimeGPT的能力
Mar 22, 2024 pm 10:10 PM
人工智慧(AI)與執法領域的融合為犯罪預防和偵查開啟了新的可能性。人工智慧的預測能力被廣泛應用於CrimeGPT(犯罪預測技術)等系統,用於預測犯罪活動。本文探討了人工智慧在犯罪預測領域的潛力、目前的應用情況、所面臨的挑戰以及相關技術可能帶來的道德影響。人工智慧和犯罪預測:基礎知識CrimeGPT利用機器學習演算法來分析大量資料集,識別可以預測犯罪可能發生的地點和時間的模式。這些資料集包括歷史犯罪統計資料、人口統計資料、經濟指標、天氣模式等。透過識別人類分析師可能忽視的趨勢,人工智慧可以為執法機構
 改進的檢測演算法:用於高解析度光學遙感影像目標檢測
Jun 06, 2024 pm 12:33 PM
改進的檢測演算法:用於高解析度光學遙感影像目標檢測
Jun 06, 2024 pm 12:33 PM
01前景概要目前,難以在檢測效率和檢測結果之間取得適當的平衡。我們研究了一種用於高解析度光學遙感影像中目標偵測的增強YOLOv5演算法,利用多層特徵金字塔、多重偵測頭策略和混合注意力模組來提高光學遙感影像的目標偵測網路的效果。根據SIMD資料集,新演算法的mAP比YOLOv5好2.2%,比YOLOX好8.48%,在偵測結果和速度之間達到了更好的平衡。 02背景&動機隨著遠感技術的快速發展,高解析度光學遠感影像已被用於描述地球表面的許多物體,包括飛機、汽車、建築物等。目標檢測在遠感影像的解釋中
 九章雲極DataCanvas多模態大模型平台的實踐與思考
Oct 20, 2023 am 08:45 AM
九章雲極DataCanvas多模態大模型平台的實踐與思考
Oct 20, 2023 am 08:45 AM
一、多模態大模型的歷史發展上圖這張照片是1956年在美國達特茅斯學院舉行的第一屆人工智慧workshop,這次會議也被認為拉開了人工智慧的序幕,與會者主要是符號邏輯學屆的前驅(除了前排中間的神經生物學家PeterMilner)。然而這套符號邏輯學理論在隨後的很長一段時間內都無法實現,甚至到80年代90年代還迎來了第一次AI寒冬期。直到最近大語言模型的落地,我們才發現真正承載這個邏輯思維的是神經網絡,神經生物學家PeterMilner的工作激發了後來人工神經網絡的發展,也正因為此他被邀請參加了這個
 演算法在 58 畫像平台建置中的應用
May 09, 2024 am 09:01 AM
演算法在 58 畫像平台建置中的應用
May 09, 2024 am 09:01 AM
一、58畫像平台建置背景首先和大家分享下58畫像平台的建造背景。 1.傳統的畫像平台傳統的想法已經不夠,建立用戶畫像平台依賴數據倉儲建模能力,整合多業務線數據,建構準確的用戶畫像;還需要數據挖掘,理解用戶行為、興趣和需求,提供演算法側的能力;最後,還需要具備數據平台能力,有效率地儲存、查詢和共享用戶畫像數據,提供畫像服務。業務自建畫像平台和中台類型畫像平台主要區別在於,業務自建畫像平台服務單條業務線,按需定制;中台平台服務多條業務線,建模複雜,提供更為通用的能力。 2.58中台畫像建構的背景58的使用者畫像
 即時加SOTA一飛沖天! FastOcc:推理更快、部署友善Occ演算法來啦!
Mar 14, 2024 pm 11:50 PM
即時加SOTA一飛沖天! FastOcc:推理更快、部署友善Occ演算法來啦!
Mar 14, 2024 pm 11:50 PM
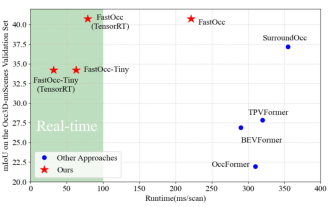
寫在前面&筆者的個人理解在自動駕駛系統當中,感知任務是整個自駕系統中至關重要的組成部分。感知任務的主要目標是使自動駕駛車輛能夠理解和感知周圍的環境元素,如行駛在路上的車輛、路旁的行人、行駛過程中遇到的障礙物、路上的交通標誌等,從而幫助下游模組做出正確合理的決策和行為。在一輛具備自動駕駛功能的車輛中,通常會配備不同類型的信息採集感測器,如環視相機感測器、雷射雷達感測器以及毫米波雷達感測器等等,從而確保自動駕駛車輛能夠準確感知和理解周圍環境要素,使自動駕駛車輛在自主行駛的過程中能夠做出正確的決斷。目






