貪心演算法(greedy algorithm)
經典的應用:例如霍夫曼編碼(Huffman Coding)、Prim 和 Kruskal 最小生成樹演算法、還有 Dijkstra 單源最短路徑演算法。
貪心演算法解決問題的步驟
第一步,當我們看到這類問題的時候,首先要聯想到貪心演算法:針對一組數據,我們定義了限制值和期望值,希望從中選出幾個數據,在滿足限制值的情況下,期望值最大。
類比到剛剛的例子,限制值就是重量不能超過 100kg,期望值就是物品的總價值。這組數據就是 5 種豆子。我們從中選出一部分,滿足重量不超過 100kg,且總價值最大。
第二步,我們試著看下這個問題是否可以用貪心演算法解決:每次選擇當前情況下,在對限制值同等貢獻量的情況下,對期望值貢獻最大的資料。
類比到剛剛的例子,我們每次都從剩下的豆子裡面,選擇單價最高的,也就是重量相同的情況下,對價值貢獻最大的豆子。
第三步,我們舉幾個例子看下貪心演算法產生的結果是否是最優的。大部分情況下,舉幾個例子來驗證一下就好了。嚴格地證明貪心演算法的正確性,是非常複雜的,需要涉及比較多的數學推理。
貪心演算法不工作的主要原因是,前面的選擇,會影響後面的選擇。
貪心演算法實戰分析
1. 分糖果
我們有 m 個糖果和 n 個孩子。我們現在要把糖果分給這些孩子吃,但是糖果少,孩子多(m 我們可以把這個問題抽象成,從 n 個孩子中,抽取一部分孩子分配糖果,讓滿足的孩子的個數(期望值)是最大的。這個問題的限制值就是糖果個數 m。
我們每次從剩下的孩子中,找出對糖果大小需求最小的,然後發給他剩下的糖果中能滿足他的最小的糖果,這樣得到的分配方案,也就是滿足的孩子個數最多的方案。
2. 錢幣找零
這個問題在我們的日常生活中更為普遍。假設我們有 1 元、2 元、5 元、10 元、20 元、50 元、100 元這些面額的紙幣,它們的張數分別是 c1、c2、c5、c10、c20、c50、c100。我們現在要用這些錢來支付 K 元,最少要用多少張紙鈔呢?
生活中,我們肯定是先用面值最大的來支付,如果不夠,就繼續用更小一點面值的,以此類推,最後剩下的用 1 元來補齊。在貢獻相同期望值(紙幣數目)的情況下,我們希望多貢獻點金額,這樣就可以讓紙幣數更少,這就是一種貪心演算法的解決思路。
3. 區間覆蓋
假設我們有 n 個區間,區間的起始端點和結束端點分別是 [l1, r1],[l2, r2],[l3, r3],…,[ln, rn]。我們從這 n 個區間中選出一部分區間,這部分區間滿足兩兩不相交(端點相交的情況不算相交),最多能選出多少個區間呢?
這個處理想法在許多貪心演算法問題中都有用到,例如任務調度、教師排課等等問題。
這個問題的解決想法是這樣的:我們假設這 n 個區間中最左端點是 lmin,最右端點是 rmax。這個問題就相當於,我們選擇幾個不相交的區間,從左到右將 [lmin, rmax] 覆蓋上。我們依照起始端點從小到大的順序對這 n 個區間排序。
我們每次選擇的時候,左端點跟前面的已經覆蓋的區間不重合的,右端點又盡量小的,這樣可以讓剩下的未覆蓋區間盡可能的大,就可以放置更多的區間。這其實就是一種貪心的選擇方法。
如何用貪心演算法實作霍夫曼編碼?
霍夫曼編碼用這種不等長的編碼方法,編碼字元。 要求各個字元的編碼之間,不會出現某個編碼是另一個編碼前綴的情況。 把出現頻率比較多的字符,用稍微短一些的編碼;出現頻率比較少的字符,用稍微長一些的編碼。
假設我有一個包含 1000 個字元的文件,每個字元佔 1 個 byte(1byte=8bits),儲存這 1000 個字元就一共需要 8000bits,那有沒有更節省空間的儲存方式呢?
假設我們透過統計分析發現,這 1000 個字符只包含 6 種不同字符,假設它們分別是 a、b、c、d、e、f。而 3 個二進位位元(bit)就可以表示 8 個不同的字符,所以,為了盡量減少儲存空間,每個字符我們用 3 個二進位位元來表示。那儲存這 1000 個字元只需要 3000bits 就可以了,比原來的儲存方式節省了很多空間。不過,還有沒有更節省空間的儲存方式呢?
a(000)、b(001)、c(010)、d(011)、e(100)、f(101)
霍夫曼編碼是一種非常有效的編碼方法,廣泛用於資料壓縮中,其壓縮率通常在 20%~90% 之間。
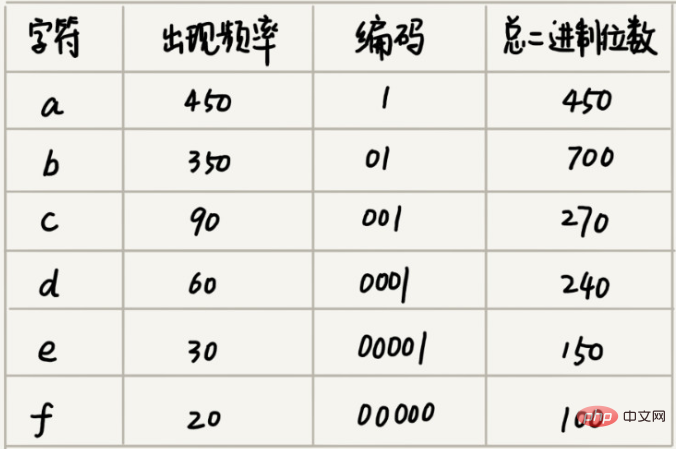
霍夫曼編碼不僅會檢視文本中有多少個不同字符,還會檢視每個字符出現的頻率,並根據頻率的不同,選擇不同長度的編碼。霍夫曼編碼試圖用這種不等長的編碼方法,進一步增加壓縮的效率。如何給不同頻率的字元選擇不同長度的編碼呢?根據貪心的思想,我們可以把出現頻率比較多的字符,用稍微短一些的編碼;出現頻率比較少的字符,用稍微長一些的編碼。
編碼不等長,如何唸出來解析?
對於等長的編碼來說,我們解壓縮起來很簡單。例如剛才那個例子中,我們用 3 個 bit 表示一個字元。在解壓縮的時候,我們每次從文字中讀取 3 位元二進位碼,然後翻譯成對應的字元。但是,霍夫曼編碼是不等長的,每次應該讀取 1 位元還是 2 位元、3 位元等等來解壓縮呢?這個問題就導致霍夫曼編碼解壓縮起來比較複雜。為了避免解壓縮過程中的歧義,霍夫曼編碼要求各個字元的編碼之間,不會出現某個編碼是另一個編碼前綴的情況。
假設這 6 個字元出現的頻率由高到低依序是 a、b、c、d、e、f。我們把它們編碼下面這個樣子,任何一個字符的編碼都不是另一個的前綴,在解壓縮的時候,我們每次會讀取盡可能長的可解壓的二進制串,所以在解壓縮的時候也不會歧義。經過這種編碼壓縮之後,這 1000 個字元只需要 2100bits 就可以了。
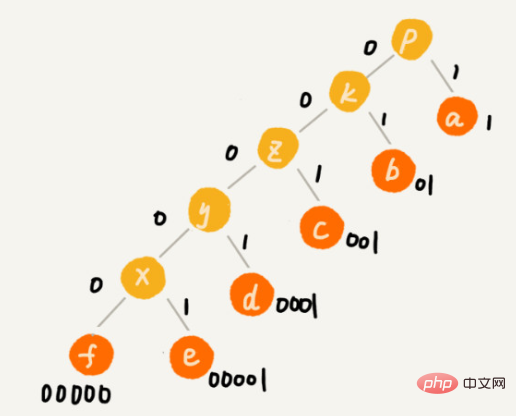
儘管霍夫曼編碼的想法並不難理解,但是如何根據字元出現頻率的不同,給不同的字元進行不同長度的編碼呢?
利用大頂堆,依照頻率放字元。
分治演算法
分治演算法(divide and conquer)的核心思想其實就是四個字,分而治之,也就是將原問題劃分成n 個規模較小,並且結構與原問題相似的子問題,遞歸地解決這些子問題,然後再合併其結果,就得到原問題的解。
分治演算法是一種處理問題的思想,遞迴是一種程式設計技巧。實際上,分治演算法一般都比較適合用遞歸來實現。分治演算法的遞歸實作中,每一層遞歸都會涉及這樣三個操作:
分解:將原始問題分解成一系列子問題; #解決:遞歸地求解各個子問題,若子問題夠小,則直接求解; 合併:將子問題的結果合併成原始問題。 分治演算法能解決的問題,一般需要滿足以下這幾個條件:
原問題與分解成的小問題具有相同的模式; #原問題分解成的子問題可以獨立求解,子問題之間沒有相關性 具有分解終止條件,也就是說,當問題足夠小時,可以直接求解; 可以將子問題合併成原問題,而這個合併操作的複雜度不能太高,否則就起不到減小演算法整體複雜度的效果了。 分治演算法應用舉例分析
如何程式求出一組資料的有序對個數或逆序對個數呢?
拿每個數字跟它後面的數字比較,看有幾個比它小的。我們把比它小的數字個數記作 k,透過這樣的方式,把每個數字都考察一遍之後,然後對每個數字對應的 k 值求和,最後得到的總和就是逆序對個數。不過,這樣操作的時間複雜度是 O(n^2)。
我們可以將陣列分成前後兩半 A1 和 A2,分別計算 A1 和 A2 的逆序對個數 K1 和 K2,然後再計算 A1 與 A2 之間的逆序對個數 K3。那數組 A 的逆序對個數就等於 K1 K2 K3。 借助歸併排序演算法
給 10GB 的訂單檔案依照金額排序這樣一個需求?
我們就可以先掃描一次訂單,依照訂單的金額,將 10GB 的檔案分成幾個金額區間。例如訂單金額為 1 到 100 元的放到一個小文件,101 到 200 之間的放到另一個文件,以此類推。這樣每個小檔案都可以單獨載入到記憶體排序,最後將這些有序的小檔案合併,就是最終有序的 10GB 訂單資料了。
回溯演算法
應用程式場景:深度優先搜索,正規表示式匹配、編譯原理中的語法分析。很多經典的數學問題都可以用回溯演算法解決,像是數獨、八皇后、0-1 背包、圖的著色、旅行商問題、全排列等等
回溯的處理思想,有點類似枚舉搜尋。我們列舉所有的解,找到滿足期望的解。為了規律地列舉所有可能的解,避免遺漏和重複,我們把問題求解的過程分成多個階段。每個階段,我們都會面對一個岔路口,我們先隨意選一條路走,當發現這條路走不通的時候(不符合期望的解),就回退到上一個岔路口,另選一種走法繼續走。
八皇后問題
我們有一個 8x8 的棋盤,希望往裡面放 8 個棋子(皇后),每個棋子所在的行、列、對角線都不能有另一個棋子。
1.0-1 背包
很多場景都可以抽象化成這個問題模型。這個問題的經典解法是動態規劃,不過還有一個簡單但沒有那麼有效率的解法,那就是今天講的回溯演算法。
我們有一個背包,背包總的承載重量是 Wkg。現在我們有 n 個物品,每個物品的重量不等,而且不可分割。我們現在期望選擇幾件物品,裝載到背包中。在不超過背包所能裝載重量的前提下,如何讓背包中物品的總重量最大?
對於每個物品來說,有兩個選擇,裝進背包或不裝進背包。對於 n 個物品來說,總的裝法就有 2^n 種,去掉總重量超過 Wkg 的,從剩下的裝法中選擇總重量最接近 Wkg 的。不過,我們要如何不重複地窮舉出這 2^n 種裝法呢?
回溯方法:我們可以把物品依序排列,整個問題就分解為了 n 個階段,每個階段對應一個物品怎麼選擇。先對第一個物品進行處理,選擇裝進去或不裝進去,再遞歸地處理剩下的物品。
動態規劃
動態規劃比較適合用來解最佳問題,例如求最大值、最小值等等。它可以非常顯著地降低時間複雜度,提高程式碼的執行效率。
0-1 背包問題
對於一組不同重量、不可分割的物品,我們需要選擇一些裝入背包,在滿足背包最大重量限制的前提下,背包中物品總重量的最大值是多少呢?
想法:
(1)把整個解題過程分成 n 個階段,每個階段會決策物品是否放到背包裡。每個物品決策(放入或不放入背包)完畢之後,背包中的物品的重量會有多種情況,也就是說,會達到多種不同的狀態,對應到遞歸樹中,就是有很多不同的節點。
(2)我們把每一層重複的狀態(節點)合併,只記錄不同的狀態,然後基於上一層的狀態集合,來推導下一層的狀態集合。我們可以透過合併每一層重複的狀態,這樣就保證每一層不同狀態的個數都不會超過 w 個(w 表示背包的承載重量),也就是例子中的 9。
分割n個階段,每一個階段都基於上一個階段推導,動態地往前推進,就避免了重複計算。
用回溯演算法解決這個問題的時間複雜度 O(2^n),是指數級的。那動態規劃解決方案的時間複雜度是多少呢?
耗時最多的部分就是程式碼中的兩層 for 循環,所以時間複雜度是 O(n*w)。 n 表示物品個數,w 表示背包可以承載的總重量。我們需要額外申請一個 n 乘以 w 1 的二維數組,對空間的消耗比較多。所以,有時候,我們會說,動態規劃是一種空間換時間的解決點子。
0-1 背包問題升級版
對於一組不同重量、不同價值、不可分割的物品,我們選擇將某些物品裝入背包,在滿足背包最大重量限制的前提下,背包中可裝入物品的總價值最大是多少呢?
什麼樣的問題適合用動態規劃來解決呢?
一個模型三個特徵
一個模型:多階段決策最佳解模型
三個特徵:
最優子結構,問題的最優解包含子問題的最優解 無後效性,第一層意義是,在推導後面階段的狀態的時候,我們只關心前面階段的狀態值,不關心這個狀態是怎麼一步一步推導出來的。第二層意義是,某階段狀態一旦確定,就不受之後階段的決策影響。 (後面的不影響前面的。) 重複子問題,不同的決策序列,到達某個相同的階段時,可能會產生重複的狀態。 兩種動態規劃解題思路總結
1. 狀態轉移表格法
一般能用動態規劃解決的問題,都可以使用回溯演算法的暴力搜尋來解決。畫出遞歸樹。從遞歸樹中,我們很容易可以看出來,是否有重複子問題,以及重複子問題是如何產生的
找到重複子問題之後,接下來,我們有兩種處理思路,第一種是直接用回溯加上「備忘錄」的方法,來避免重複子問題。從執行效率上來講,這跟動態規劃的解決思路沒有差異。第二種是使用動態規劃的解法,狀態轉移表法。
我們先畫出一個狀態表。狀態表通常都是二維的,所以你可以把它想像成二維數組。其中,每個狀態包含三個變量,行、列、數組值。我們根據決策的先後過程,從前往後,根據遞推關係,分階段填入狀態表中的每個狀態。最後,我們將這個遞推填表的過程,翻譯成程式碼,就是動態規劃程式碼了。
需要很多變數來表示,那對應的狀態表可能就是高維度的,例如三維、四維。那這個時候,我們就不適合用狀態轉移表法來解決了。一方面是因為高維度狀態轉移表不好畫圖表示,另一方面是因為人腦確實很不擅長思考高維度的東西。
2. 狀態轉移方程式法
我們需要分析,某個問題如何透過子問題來遞迴求解,也就是所謂的最佳子結構。根據最優子結構,寫出遞歸公式,也就是所謂的狀態轉移方程式。有了狀態轉移方程,程式碼實作就非常簡單了。一般情況下,我們有兩種程式碼實作方法,一種是遞迴加上「備忘錄」,另一種是迭代遞推。
min_dist(i, j) = w[i][j] min(min_dist(i, j-1), min_dist(i-1, j))
我要強調一點,不是每個問題都同時適合這兩種解題想法。有的問題可能用第一種思路比較清晰,而有的問題可能用第二種思路比較清晰,所以,你要結合具體的題目來看,到底選擇用哪種解題思路。 狀態轉移表法解題思路大致可以概括為,回溯演算法實現- 定義狀態- 畫遞歸樹- 找重複子問題- 畫狀態轉移表- 根據遞推關係填表- 將填表過程翻譯成代碼。 狀態轉移方程法的大致思路可以概括為,找最優子結構 - 寫入狀態轉移方程式 - 將狀態轉移方程式翻譯成程式碼。
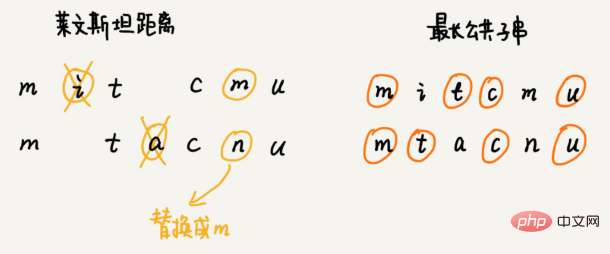
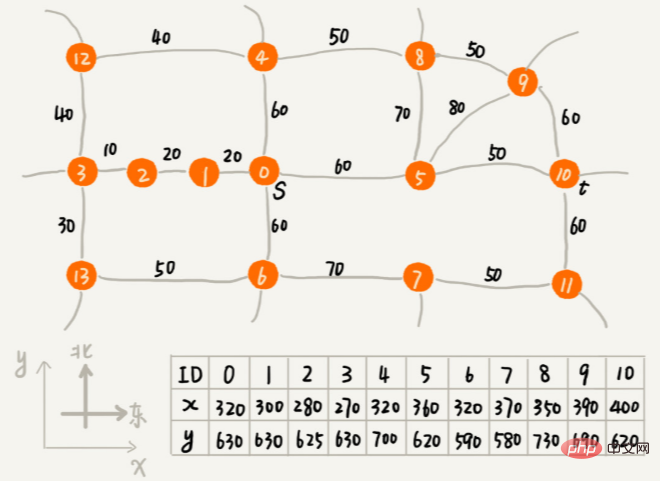
如何量化兩個字串的相似度? 編輯距離指的就是,將字串轉換成另一個字串,所需的最少編輯操作次數(例如增加一個字元、刪除一個字元、替換一個字元)。編輯距離越大,表示兩個字串的相似程度越小;相反,編輯距離就越小,表示兩個字串的相似程度越大。對於兩個完全相同的字串來說,編輯距離就是 0。 編輯距離有多種不同的計算方式,比較著名的有萊文斯坦距離(Levenshtein distance)和最長公共子字串長度(Longest common substring length) 。其中,萊文斯坦距離允許增加、刪除、替換字元這三個編輯操作,最長公共子字串長度只允許增加、刪除字元這兩個編輯操作。 萊文斯坦距離和最長公共子字串長度,從兩個截然相反的角度,分析字串的相似程度。萊文斯坦距離的大小,表示兩個字串差異的大小;而最長公共子字串的大小,表示兩個字串相似程度的大小。 兩個字串 mitcmu 和 mtacnu 的萊文斯坦距離是 3,最長公共子字串長度是 4。 如何程式計算萊文斯坦距離? 這個問題是求把一個字串變成另一個字串,需要的最少編輯次數。整個求解過程,涉及多個決策階段,我們需要依次考察一個字符串中的每個字符,跟另一個字符串中的字符是否匹配,匹配的話如何處理,不匹配的話又如何處理。所以,這個問題符合多階段決策最佳解模型。 推薦演算法 利用向量的距離,求相似成度。 搜尋:如何用A*搜尋演算法實現遊戲中的尋路功能? 那要如何快速找出一條接近最短路線的次優路線呢? 這個快速的路徑規劃演算法,就是我們今天要學習的A* 演算法。實際上,A* 演算法是對 Dijkstra 演算法的最佳化和改造。 透過這個頂點跟終點之間的直線距離,也就是歐幾里德距離來近似地估計這個頂點跟終點的路徑長度(注意:路徑長度跟直線距離是兩個概念) 這個距離記作h(i)(i 表示這個頂點的編號),專業的叫法是啟發函數(heuristic function) 因為歐幾里德距離的計算公式,會涉及比較耗時的開根號計算,所以,我們一般通過另一個更簡單的距離計算公式,那就是曼哈頓距離(Manhattan distance) 曼哈頓距離是兩點之間橫縱座標的距離總和。計算的過程只涉及加減法、符號位反轉,所以比歐幾里德距離更有效率。 int hManhattan(Vertex v1, Vertex v2) { // Vertex 表示頂點,後面有定義
return Math.abs(v1.x - v2.x) Math.abs(v1.y - v2.y);
}
f(i)=g(i) h(i),頂點與起點之間的路徑長度g(i),頂點到終點的路徑長度估計值h(i). f(i)的專業叫法是估價函數(evaluation function)。 A* 演算法就是 Dijkstra 演算法的簡單改造, f(i) 最小的先出列。 它跟 Dijkstra 演算法的程式碼實現,主要有 3 點差異: 優先權佇列建構的方式不同。 A* 演算法是根據f 值(也就是剛剛講到的f(i)=g(i) h(i))來建構優先權隊列,而Dijkstra 演算法是根據dist 值(也就是剛剛講到的g( i))來建構優先權佇列; A* 演算法在更新頂點dist 值的時候,會同步更新f 值; 循環結束的條件也不一樣。 Dijkstra 演算法是在終點出佇列的時候才結束,A* 演算法是一旦遍歷到終點就結束。 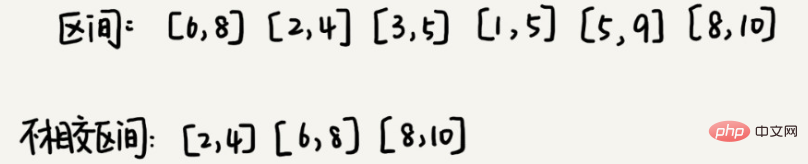
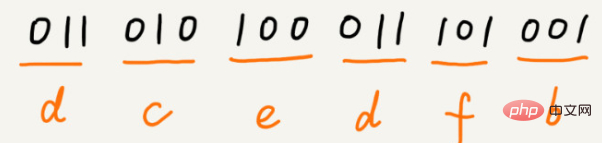
 #
#
 #
#
#
以上是有哪些常見的演算法是Java開發中常用的呢?的詳細內容。更多資訊請關注PHP中文網其他相關文章!




