怎麼用Python求矩陣的範數和行列式
在scipy.linalg的函數中,往往會提供兩種參數,其一是check_finite,當為True時將進行有限檢查,另一類是overwrite_xxxx,表示xxxx在計算過程中是否可以被覆寫。簡潔起見,後文說a提供覆寫開關,就表示存在一個參數overwrite_a,當其為True時,a允許計算過程中被覆寫;若說提供有限檢查開關,則代表提供check_finite參數。
範數
在scipy.linalg中提供了函數norm用來求範數,其定義為
norm(a, ord=None, axis=None, keepdims=False, check_finite=True)
其中ord用來宣告範數的階
| ord | 矩陣範數 | 向量範數 |
|---|---|---|
| None | 弗羅貝尼烏斯範數 | |
| 'fro' | 弗羅貝尼烏斯範數 |
| 'nuc' | #核範數 |
inf | #max(sum(abs(a), axis=1)) | |
#-inf | min(sum(abs(a), axis=1)) | |
| #0 | ##- | #sum(a!= 0)|
1 | max(sum(abs(a), axis=0))||
-1 | min(sum(abs(a), axis=0))||
| 2 | 2-範數(最大奇異值) | |
| -2 | 最小奇異值 |
# 若a為向量,若
為非零整數,記作n nn,設a i a_iai為矩陣a aa中的元素,則矩陣的n nn範數為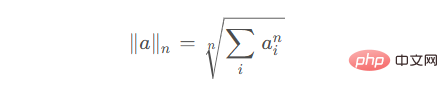
#數又稱「跡範數」 (trace norm),表示矩陣的所有奇異值總和。
Frobenius範數可定義為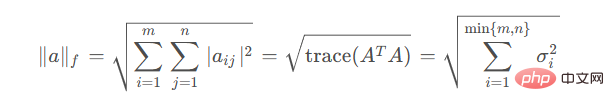
其實質是向量的2-範數在矩陣中的自然推廣。 除了scipy.linalg之外,numpy.linalg中也提供了
,其參數為<div class="code" style="position:relative; padding:0px; margin:0px;"><pre class='brush:php;toolbar:false;'>norm(x, ord=None, axis=None, keepdims=False)</pre><div class="contentsignin">登入後複製</div></div>其中order的可選參數與scipy.linalg中的
函數相同。
行列式在scipy.linalg中,行列式函數為det,其定義非常簡單,除了待求矩陣 a之外,就只有
的覆寫開關和有限檢查。
範例如下
import numpy as np from scipy import linalg a = np.array([[1,2,3], [4,5,6], [7,8,9]]) linalg.det(a) # 0.0 a = np.array([[0,2,3], [4,5,6], [7,8,9]]) linalg.det(a) # 3.0
跡scipy.linalg不提供trace函數,但
提供,其定義為
umpy.trace(a, offset=0, axis1=0, axis2=1, dtype=None, out=None)
- 其中
offset 為偏移量,表示相對於主對角線的偏移-
axis1, axis2 表示座標軸
dtype 用於調整輸出值的資料類型
>>> x = np.random.rand(3,3) >>> print(x) [[0.26832187 0.64615363 0.09006217] [0.63106319 0.65573765 0.35842304] [0.66629322 0.16999836 0.92357658]] >>> np.trace(x) 1.8476361016546932
以上是怎麼用Python求矩陣的範數和行列式的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

熱門話題
 mysql 是否要付費
Apr 08, 2025 pm 05:36 PM
mysql 是否要付費
Apr 08, 2025 pm 05:36 PM
MySQL 有免費的社區版和收費的企業版。社區版可免費使用和修改,但支持有限,適合穩定性要求不高、技術能力強的應用。企業版提供全面商業支持,適合需要穩定可靠、高性能數據庫且願意為支持買單的應用。選擇版本時考慮的因素包括應用關鍵性、預算和技術技能。沒有完美的選項,只有最合適的方案,需根據具體情況謹慎選擇。
 PS羽化如何控製過渡的柔和度?
Apr 06, 2025 pm 07:33 PM
PS羽化如何控製過渡的柔和度?
Apr 06, 2025 pm 07:33 PM
羽化控制的關鍵在於理解其漸變本質。 PS本身不提供直接控制漸變曲線的選項,但你可以通過多次羽化、配合蒙版、精細選區,靈活調整半徑和漸變柔和度,實現自然過渡效果。
 mysql安裝後怎麼使用
Apr 08, 2025 am 11:48 AM
mysql安裝後怎麼使用
Apr 08, 2025 am 11:48 AM
文章介紹了MySQL數據庫的上手操作。首先,需安裝MySQL客戶端,如MySQLWorkbench或命令行客戶端。 1.使用mysql-uroot-p命令連接服務器,並使用root賬戶密碼登錄;2.使用CREATEDATABASE創建數據庫,USE選擇數據庫;3.使用CREATETABLE創建表,定義字段及數據類型;4.使用INSERTINTO插入數據,SELECT查詢數據,UPDATE更新數據,DELETE刪除數據。熟練掌握這些步驟,並學習處理常見問題和優化數據庫性能,才能高效使用MySQL。
 PS羽化怎麼設置?
Apr 06, 2025 pm 07:36 PM
PS羽化怎麼設置?
Apr 06, 2025 pm 07:36 PM
PS羽化是一種圖像邊緣模糊效果,通過在邊緣區域對像素加權平均實現。設置羽化半徑可以控制模糊程度,數值越大越模糊。靈活調整半徑可根據圖像和需求優化效果,如處理人物照片時使用較小半徑保持細節,處理藝術作品時使用較大半徑營造朦朧感。但需注意,半徑過大易丟失邊緣細節,過小則效果不明顯。羽化效果受圖像分辨率影響,且需要根據圖像理解和效果把握進行調整。
 mysql下載文件損壞無法安裝的修復方案
Apr 08, 2025 am 11:21 AM
mysql下載文件損壞無法安裝的修復方案
Apr 08, 2025 am 11:21 AM
MySQL下載文件損壞,咋整?哎,下載個MySQL都能遇到文件損壞,這年頭真是不容易啊!這篇文章就來聊聊怎麼解決這個問題,讓大家少走彎路。讀完之後,你不僅能修復損壞的MySQL安裝包,還能對下載和安裝過程有更深入的理解,避免以後再踩坑。先說說為啥下載文件會損壞這原因可多了去了,網絡問題是罪魁禍首,下載過程中斷、網絡不穩定都可能導致文件損壞。還有就是下載源本身的問題,服務器文件本身就壞了,你下載下來當然也是壞的。另外,一些殺毒軟件過度“熱情”的掃描也可能造成文件損壞。診斷問題:確定文件是否真的損壞
 mySQL下載完安裝不了
Apr 08, 2025 am 11:24 AM
mySQL下載完安裝不了
Apr 08, 2025 am 11:24 AM
MySQL安裝失敗的原因主要有:1.權限問題,需以管理員身份運行或使用sudo命令;2.依賴項缺失,需安裝相關開發包;3.端口衝突,需關閉佔用3306端口的程序或修改配置文件;4.安裝包損壞,需重新下載並驗證完整性;5.環境變量配置錯誤,需根據操作系統正確配置環境變量。解決這些問題,仔細檢查每個步驟,就能順利安裝MySQL。
 mysql安裝後怎麼優化數據庫性能
Apr 08, 2025 am 11:36 AM
mysql安裝後怎麼優化數據庫性能
Apr 08, 2025 am 11:36 AM
MySQL性能優化需從安裝配置、索引及查詢優化、監控與調優三個方面入手。 1.安裝後需根據服務器配置調整my.cnf文件,例如innodb_buffer_pool_size參數,並關閉query_cache_size;2.創建合適的索引,避免索引過多,並優化查詢語句,例如使用EXPLAIN命令分析執行計劃;3.利用MySQL自帶監控工具(SHOWPROCESSLIST,SHOWSTATUS)監控數據庫運行狀況,定期備份和整理數據庫。通過這些步驟,持續優化,才能提升MySQL數據庫性能。
 如何針對高負載應用程序優化 MySQL 性能?
Apr 08, 2025 pm 06:03 PM
如何針對高負載應用程序優化 MySQL 性能?
Apr 08, 2025 pm 06:03 PM
MySQL數據庫性能優化指南在資源密集型應用中,MySQL數據庫扮演著至關重要的角色,負責管理海量事務。然而,隨著應用規模的擴大,數據庫性能瓶頸往往成為製約因素。本文將探討一系列行之有效的MySQL性能優化策略,確保您的應用在高負載下依然保持高效響應。我們將結合實際案例,深入講解索引、查詢優化、數據庫設計以及緩存等關鍵技術。 1.數據庫架構設計優化合理的數據庫架構是MySQL性能優化的基石。以下是一些核心原則:選擇合適的數據類型選擇最小的、符合需求的數據類型,既能節省存儲空間,又能提升數據處理速度






