(1) 單位矩陣
#即主對角線上的元素皆為1,其餘元素皆為0的正方形矩陣。
在NumPy中可以用eye函數建立一個這樣的二維數組,我們只需要給定一個參數,用於指定矩陣中1的元素個數。
例如,建立3×3的陣列:
import numpy as np I2 = np.eye(3) print(I2) [[1. 0. 0.] [0. 1. 0.] [0. 0. 1.]]
(2) 使用savetxt函數將資料儲存到檔案中,當然我們需要指定檔案名稱以及要儲存的陣列。
np.savetxt('eye.txt', I2)#创建一个eye.txt文件,用于保存I2的数据
CSV(Comma-Separated Value,逗號分隔值)格式是常見的檔案格式;通常,資料庫的轉存文件就是CSV格式的,文件中的各個欄位對應資料庫表中的欄位;電子表格軟體(如Microsoft Excel)可以處理CSV文件。
note: ,NumPy中的loadtxt函數可以方便地讀取CSV文件,自動切分字段,並將資料載入NumPy數組
data.csv的資料內容:
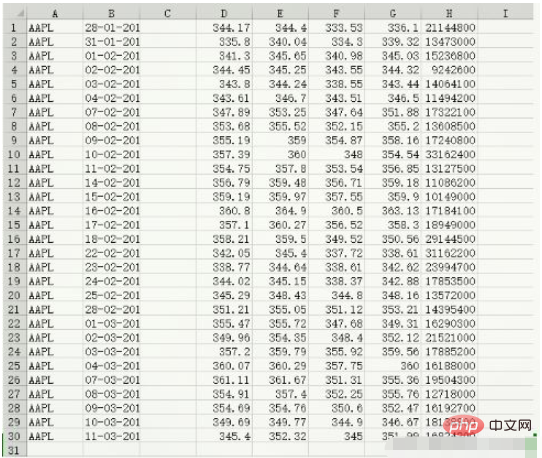
c, v = np.loadtxt('data.csv', delimiter=',', usecols=(6,7), unpack=True) # usecols的参数为一个元组,以获取第7字段至第8字段的数据 # unpack参数设置为True,意思是分拆存储不同列的数据,即分别将收盘价和成交量的数组赋值给变量c和v print(c) [336.1 339.32 345.03 344.32 343.44 346.5 351.88 355.2 358.16 354.54 356.85 359.18 359.9 363.13 358.3 350.56 338.61 342.62 342.88 348.16 353.21 349.31 352.12 359.56 360. 355.36 355.76 352.47 346.67 351.99] print(v) [21144800. 13473000. 15236800. 9242600. 14064100. 11494200. 17322100. 13608500. 17240800. 33162400. 13127500. 11086200. 10149000. 17184100. 18949000. 29144500. 31162200. 23994700. 17853500. 13572000. 14395400. 16290300. 21521000. 17885200. 16188000. 19504300. 12718000. 16192700. 18138800. 16824200.] print(type(c)) print(type(v)) <class 'numpy.ndarray'> <class 'numpy.ndarray'>
VWAP概述:VWAP(Volume- Weighted Average Price,成交量加權平均價格)是一個非常重要的經濟學量,它代表金融資產的「平均」價格。
某個價格的成交量越高,該價格所佔的權重就越大。
VWAP就是以成交量為權重計算出來的加權平均值,常用於演算法交易。
vwap = np.average(c,weights=v) print('成交量加权平均价格vwap =', vwap) 成交量加权平均价格vwap = 350.5895493532009
NumPy中的mean函數可以計算陣列元素的算術平均值
print('c数组中元素的算数平均值为: {}'.format(np.mean(c)))
c数组中元素的算数平均值为: 351.0376666666667TWAP概述:
在經濟學中,TWAP(Time-Weighted Average Price,時間加權平均價格)是另一種“平均”價格的指標。既然我們已經計算了VWAP,那也來計算一下TWAP吧。其實TWAP只是一個變種而已,基本的想法就是最近的價格重要性大一些,所以我們應該對近期的價格給予較高的權重。最簡單的方法就是用arange函數建立一個從0開始依序成長的自然數序列,自然數的數量即為收盤價的數目。當然,這不一定是正確的計算TWAP的方式。
t = np.arange(len(c)) print('时间加权平均价格twap=', np.average(c, weights=t)) 时间加权平均价格twap= 352.4283218390804
h, l = np.loadtxt('data.csv', delimiter=',', usecols=(4,5), unpack=True)
print('h数据为: \n{}'.format(h))
print('-'*10)
print('l数据为: \n{}'.format(l))
h数据为:
[344.4 340.04 345.65 345.25 344.24 346.7 353.25 355.52 359. 360.
357.8 359.48 359.97 364.9 360.27 359.5 345.4 344.64 345.15 348.43
355.05 355.72 354.35 359.79 360.29 361.67 357.4 354.76 349.77 352.32]
----------
l数据为:
[333.53 334.3 340.98 343.55 338.55 343.51 347.64 352.15 354.87 348.
353.54 356.71 357.55 360.5 356.52 349.52 337.72 338.61 338.37 344.8
351.12 347.68 348.4 355.92 357.75 351.31 352.25 350.6 344.9 345. ]
print('h数据的最大值为: {}'.format(np.max(h)))
print('l数据的最小值为: {}'.format(np.min(l)))
h数据的最大值为: 364.9
l数据的最小值为: 333.53
NumPy中有一个ptp函数可以计算数组的取值范围
该函数返回的是数组元素的最大值和最小值之间的差值
也就是说,返回值等于max(array) - min(array)
print('h数据的最大值-最小值的差值为: \n{}'.format(np.ptp(h)))
print('l数据的最大值-最小值的差值为: \n{}'.format(np.ptp(l)))
h数据的最大值-最小值的差值为:
24.859999999999957
l数据的最大值-最小值的差值为:
26.970000000000027中位數:我們可以用有些閾值來除去異常值,但其實有更好的方法,那就是中位數。
將各個變數值依大小順序排列起來,形成一個數列,居於數列中間位置的那個數即為中位數。
例如,我們有1、2、3、4、5這5個數值,那麼中位數就是中間的數字3。
m = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
print('m数据中的中位数为: {}'.format(np.median(m)))
m数据中的中位数为: 352.055
# 数组排序后,查找中位数
sorted_m = np.msort(m)
print('m数据排序: \n{}'.format(sorted_m))
N = len(c)
print('m数据中的中位数为: {}'.format((sorted_m[N//2]+sorted_m[(N-1)//2])/2))
m数据排序:
[336.1 338.61 339.32 342.62 342.88 343.44 344.32 345.03 346.5 346.67
348.16 349.31 350.56 351.88 351.99 352.12 352.47 353.21 354.54 355.2
355.36 355.76 356.85 358.16 358.3 359.18 359.56 359.9 360. 363.13]
m数据中的中位数为: 352.055
方差:
方差是指各个数据与所有数据算术平均数的离差平方和除以数据个数所得到的值。
print('variance =', np.var(m))
variance = 50.126517888888884
var_hand = np.mean((m-m.mean())**2)
print('var =', var_hand)
var = 50.126517888888884注意:樣本變異數和總體變異數在計算上的差異。總體變異數是用資料個數去除離差平方和,而樣本變異數則是用樣本資料個數減1去除離差平方和,其中樣本資料個數減1(即n-1)稱為自由度。之所以有這樣的差別,是為了確保樣本變異數是無偏估計量。
在學術文獻中,收盤價的分析常常是基於股票報酬率和對數報酬率的。
簡單收益率是指相鄰兩個價格之間的變化率,而對數收益率是指所有價格取對數後兩兩之間的差值。
我們在高中學過對數的知識,「a」的對數減去「b」的對數就等於「a除以b」的對數。因此,對數收益率也可以用來衡量價格的變化率。
注意,由於收益率是一個比值,例如我們用美元除以美元(也可以是其他貨幣單位),因此它是無量綱的。
總之,投資人最感興趣的是收益率的變異數或標準差,因為這代表著投資風險的大小。
(1) 首先,我們來計算簡單報酬率。 NumPy中的diff函數可以傳回由相鄰陣列元素的差值所構成的陣列。這有點類似微積分中的微分。為了計算收益率,我們還需要用差值來除以前一天的價格。不過這裡要注意,diff傳回的陣列比收盤價數組少一個元素。 returns = np.diff(arr)/arr[:-1]
注意,我們沒有用收盤價數組中的最後一個值做除數。接下來,用std函數計算標準差:
print ("Standard deviation =", np.std(returns))(2) 對數收益率計算起來甚至更簡單一些。我們先用log函數得到每一個收盤價的對數,再對結果使用diff函數即可。
logreturns = np.diff( np.log(c) )
一般情況下,我們應檢查輸入陣列以確保其不含有零和負數。否則,將得到一個錯誤提示。不過在我們的例子中,股價總為正值,所以可以將檢查省略掉。
(3) 我們很可能對哪些交易日的收益率為正值非常感興趣。
在完成了前面的步驟之後,我們只需要用where函數就可以做到這一點。 where函數可以根據指定的條件傳回所有滿足條件的陣列元素的索引值。
輸入如下程式碼:
posretindices = np.where(returns > 0) print "Indices with positive returns", posretindices 即可输出该数组中所有正值元素的索引。 Indices with positive returns (array([ 0, 1, 4, 5, 6, 7, 9, 10, 11, 12, 16, 17, 18, 19, 21, 22, 23, 25, 28]),)
(4) 在投资学中,波动率(volatility)是对价格变动的一种度量。历史波动率可以根据历史价格数据计算得出。计算历史波动率(如年波动率或月波动率)时,需要用到对数收益率。年波动率等于对数收益率的标准差除以其均值,再除以交易日倒数的平方根,通常交易日取252天。用std和mean函数来计算
代码如下所示:
annual_volatility = np.std(logreturns)/np.mean(logreturns) annual_volatility = annual_volatility / np.sqrt(1./252.)
(5) sqrt函数中的除法运算。在Python中,整数的除法和浮点数的除法运算机制不同(python3已修改该功能),我们必须使用浮点数才能得到正确的结果。与计算年波动率的方法类似,计算月波动率如下:
annual_volatility * np.sqrt(1./12.)
c = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
returns = np.diff(c)/c[:-1]
print('returns的标准差: {}'.format(np.std(returns)))
logreturns = np.diff(np.log(c))
posretindices = np.where(returns>0)
print('retruns中元素为正数的位置: \n{}'.format(posretindices))
annual_volatility = np.std(logreturns)/np.mean(logreturns)
annual_volatility = annual_volatility/np.sqrt(1/252)
print('每年波动率: {}'.format(annual_volatility))
print('每月波动率:{}'.format(annual_volatility*np.sqrt(1/12)))
returns的标准差: 0.012922134436826306
retruns中元素为正数的位置:
(array([ 0, 1, 4, 5, 6, 7, 9, 10, 11, 12, 16, 17, 18, 19, 21, 22, 23,
25, 28], dtype=int64),)
每年波动率: 129.27478991115132
每月波动率:37.318417377317765以上是Python常用函數中的NumPy怎麼使用的詳細內容。更多資訊請關注PHP中文網其他相關文章!




