1. 算術運算表達式求值
#要解析這類文本，需要另外一種特定的語法規則。我們在這裡介紹可以表示上下文無關文法（context free grammer）的語法規則巴科斯範式(BNF)和擴展巴科斯範式(EBNF)。從小到一個算術運算表達式，到大到幾乎所有程式設計語言，都是利用上下文無關文法來定義的。
對於簡單的算術運算表達式，假定我們已經用分詞技術將其轉換為輸入的tokens流，如NUM NUM*NUM（分詞方法參見上一篇博文）。
在此基礎上，我們定義BNF規則定義如下：
expr ::= expr + term
| expr - term
| term
term ::= term * factor
| term / factor
| factor
factor ::= (expr)
| NUM登入後複製
當然，這種計法還不夠簡潔明了，我們實際採用的為EBNF形式：
expr ::= term { (+|-) term }*
term ::= factor { (*|/) factor }*
factor ::= (expr)
| NUM登入後複製
BNF和EBNF每一條規則(形如::=的式子)都可以看做是一種替換，即左側的符號可以被右側的符號所替換。我們在解析過程中嘗試使用BNF/EBNF將輸入文字與語法規則進行匹配，以完成各種替換和擴展。在EBNF中，被放置在{...}*內的規則是可選的，而*則表示可以重複零次或多次（類比於正規表示式）。
下圖形像地展示了遞歸下降解析器(parser)中「遞歸」和「下降」部分和ENBF的關係：
##在實際的解析過程中，我們對tokens流從左到右進行掃描，在掃描的過程中處理token，如果卡住就產生一個語法錯誤。每個語法規則都被轉換為一個函數或方法，例如上面的ENBF規則被轉換成下述方法：
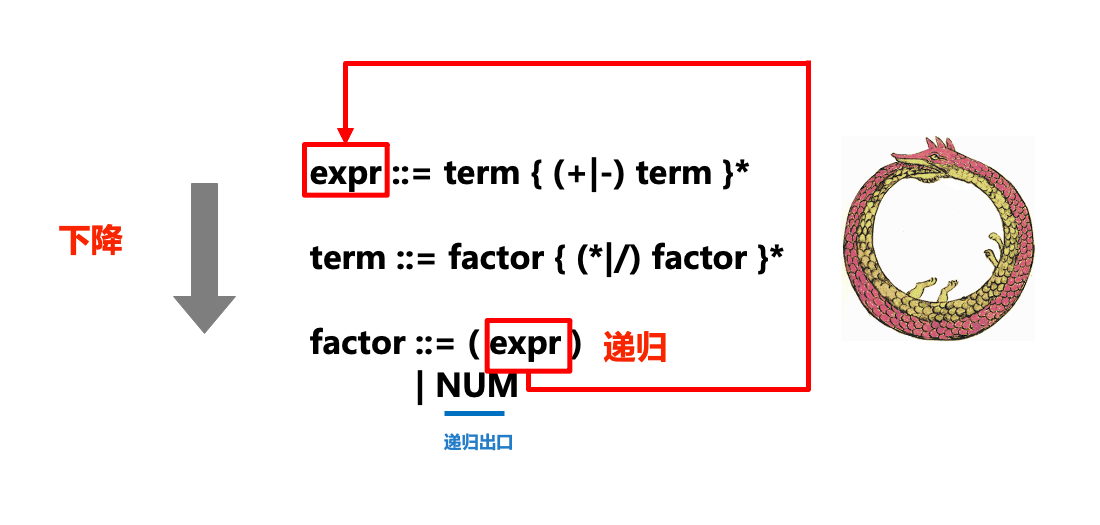
class ExpressionEvaluator():
...
def expr(self):
...
def term(self):
...
def factor(self):
...登入後複製
在呼叫某個規則對應方法的過程中，如果我們發現接下來的符號需要採用另一個規則來匹配，則我們就會「下降」到另一個規則方法（如在expr中呼叫term，term中呼叫factor），則也就是遞迴下降中「下降」的部分。
有時也會呼叫已經在執行的方法（例如在expr中呼叫term，term中呼叫factor後，又在factor中呼叫expr，相當於一條銜尾蛇），這也就是遞歸下降中“遞迴”的部分。
對於語法中出現的重複部分（例如
expr ::= term { ( |-) term }*），我們則透過while循環來實現。
下面我們來看具體的程式碼實作。首先是分詞部分，我們參考上一篇介紹分詞部落格的程式碼。
import re
import collections
# 定义匹配token的模式
NUM = r'(?P<NUM>\d+)' # \d表示匹配数字，+表示任意长度
PLUS = r'(?P<PLUS>\+)' # 注意转义
MINUS = r'(?P<MINUS>-)'
TIMES = r'(?P<TIMES>\*)' # 注意转义
DIVIDE = r'(?P<DIVIDE>/)'
LPAREN = r'(?P<LPAREN>\()' # 注意转义
RPAREN = r'(?P<RPAREN>\))' # 注意转义
WS = r'(?P<WS>\s+)' # 别忘记空格，\s表示空格，+表示任意长度
master_pat = re.compile(
'|'.join([NUM, PLUS, MINUS, TIMES, DIVIDE, LPAREN, RPAREN, WS]))
# Tokenizer
Token = collections.namedtuple('Token', ['type', 'value'])
def generate_tokens(text):
scanner = master_pat.scanner(text)
for m in iter(scanner.match, None):
tok = Token(m.lastgroup, m.group())
if tok.type != 'WS': # 过滤掉空格符
yield tok登入後複製
以下是表達式求值器的具體實作：
class ExpressionEvaluator():
""" 递归下降的Parser实现，每个语法规则都对应一个方法，
使用 ._accept()方法来测试并接受当前处理的token，不匹配不报错，
使用 ._except()方法来测试当前处理的token，并在不匹配的时候抛出语法错误
"""
def parse(self, text):
""" 对外调用的接口 """
self.tokens = generate_tokens(text)
self.tok, self.next_tok = None, None # 已匹配的最后一个token，下一个即将匹配的token
self._next() # 转到下一个token
return self.expr() # 开始递归
def _next(self):
""" 转到下一个token """
self.tok, self.next_tok = self.next_tok, next(self.tokens, None)
def _accept(self, tok_type):
""" 如果下一个token与tok_type匹配，则转到下一个token """
if self.next_tok and self.next_tok.type == tok_type:
self._next()
return True
else:
return False
def _except(self, tok_type):
""" 检查是否匹配，如果不匹配则抛出异常 """
if not self._accept(tok_type):
raise SyntaxError("Excepted"+tok_type)
# 接下来是语法规则，每个语法规则对应一个方法
def expr(self):
""" 对应规则： expression ::= term { ('+'|'-') term }* """
exprval = self.term() # 取第一项
while self._accept("PLUS") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.term()
if op == "PLUS":
exprval += right
elif op == "MINUS":
exprval -= right
return exprval
def term(self):
""" 对应规则： term ::= factor { ('*'|'/') factor }* """
termval = self.factor() # 取第一项
while self._accept("TIMES") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.factor()
if op == "TIMES":
termval *= right
elif op == "DIVIDE":
termval /= right
return termval
def factor(self):
""" 对应规则： factor ::= NUM | ( expr ) """
if self._accept("NUM"): # 递归出口
return int(self.tok.value)
elif self._accept("LPAREN"):
exprval = self.expr() # 继续递归下去求表达式值
self._except("RPAREN") # 别忘记检查是否有右括号，没有则抛出异常
return exprval
else:
raise SyntaxError("Expected NUMBER or LPAREN")登入後複製
我們輸入以下表達式進行測試：
e = ExpressionEvaluator()
print(e.parse("2"))
print(e.parse("2+3"))
print(e.parse("2+3*4"))
print(e.parse("2+(3+4)*5"))登入後複製
求值結果如下：
25
14
37
如果我們輸入的文字不符合語法規則：
print(e.parse("2 + (3 + * 4)"))登入後複製
則會拋出SyntaxError例外：
Expected NUMBER or LPAREN。 綜上，可見我們的表達式求值演算法運行正確。
2. 產生表達式樹
上面我們是得到表達式的結果，但是如果我們想要分析表達式的結構，產生一棵簡單的表達式解析樹呢？那我們需要對上述類別的方法做一定修改：
class ExpressionTreeBuilder(ExpressionEvaluator):
def expr(self):
""" 对应规则： expression ::= term { ('+'|'-') term }* """
exprval = self.term() # 取第一项
while self._accept("PLUS") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.term()
if op == "PLUS":
exprval = ('+', exprval, right)
elif op == "MINUS":
exprval -= ('-', exprval, right)
return exprval
def term(self):
""" 对应规则： term ::= factor { ('*'|'/') factor }* """
termval = self.factor() # 取第一项
while self._accept("TIMES") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.factor()
if op == "TIMES":
termval = ('*', termval, right)
elif op == "DIVIDE":
termval = ('/', termval, right)
return termval
def factor(self):
""" 对应规则： factor ::= NUM | ( expr ) """
if self._accept("NUM"): # 递归出口
return int(self.tok.value) # 字符串转整形
elif self._accept("LPAREN"):
exprval = self.expr() # 继续递归下去求表达式值
self._except("RPAREN") # 别忘记检查是否有右括号，没有则抛出异常
return exprval
else:
raise SyntaxError("Expected NUMBER or LPAREN")登入後複製
輸入下列表達式測試一下：
print(e.parse("2+3"))
print(e.parse("2+3*4"))
print(e.parse("2+(3+4)*5"))
print(e.parse('2+3+4'))登入後複製
以下是產生結果：
(' ' , 2, 3)(' ', 2, ('*', 3, 4))
(' ', 2, ('*', (' ', 3, 4), 5))
(' ', (' ', 2, 3), 4)
可以看到表達式樹產生正確。
我們上面的這個例子非常簡單，但遞歸下降的解析器也可以用來實現相當複雜的解析器，例如Python程式碼就是透過一個遞歸下降解析器解析的。您要是對此跟感興趣可以檢查Python原始碼中的
Grammar檔案來一探究竟。然而，下面我們接著會看到，自己動手寫一個解析器會面對各種陷阱和挑戰。
左遞歸和運算子優先級陷阱
任何涉及
左遞歸形式的語法規則，都沒法用遞歸下降parser來解決。所謂左遞歸，即規則式子右側最左邊的符號是規則頭，例如對於以下規則：
items ::= items ',' item
| item登入後複製
完成該解析你可能會定義以下方法：
def items(self):
itemsval = self.items() # 取第一项，然而此处会无穷递归！
if itemsval and self._accept(','):
itemsval.append(self.item())
else:
itemsval = [self.item()]登入後複製
這樣做會在第一行就無窮地呼叫
self.items()從而產生無窮遞歸錯誤。
還有一種是語法規則本身的錯誤，例如運算子優先權。我們如果忽略運算子優先權直接將表達式簡化如下：
expr ::= factor { ('+'|'-'|'*'|'/') factor }*
factor ::= '(' expr ')'
| NUM登入後複製
PYTHON 複製全螢幕
這個語法從技術上可以實現，但是沒有遵守計算順序約定，導致"3 4* 5"的運算結果為35，而非預期的23。因此，需要使用單獨的expr和term規則來確保計算結果的正確性。
以上是Python遞歸下降Parser怎麼實現的詳細內容。更多資訊請關注PHP中文網其他相關文章！
