儘管 DNN 在各種實際應用中取得了廣泛的成功,但其過程通常被視為黑盒子,因為我們很難解釋 DNN 如何做出決定。缺乏可解釋性損害了 DNN 的可靠性,從而阻礙了它們在高風險任務中的廣泛應用,例如自動駕駛和 AI 醫療。因此,可以解釋 DNN 引起了越來越多的關注。
作為解釋 DNN 的典型視角,歸因方法旨在計算每個輸入變數對網路輸出的歸因 / 重要性 / 貢獻分數。例如,給定一個用於影像分類的預訓練 DNN 和一個輸入影像,每個輸入變數的屬性得分是指每個像素對分類置信度得分的數值影響。
儘管近年來研究者提出了許多歸因方法,但大多數都建立在不同的啟發式方法之上。目前還缺乏統一的理論觀點來檢驗這些歸因方法的正確性,或至少在數學上闡明其核心機制。
研究者曾試圖統一不同的歸因方法,但這些研究只涵蓋了幾種方法。
本文中,我們提出了「統一解釋 14 種輸入單元重要性歸因演算法的內在機制」。

論文網址:https://arxiv.org/pdf/2303.01506.pdf
#其實無論是「12 種提升對抗遷移性的演算法」,或是「14 種輸入單元重要性歸因演算法」,都是工程演算法的重災區。在這兩大領域內,大部分演算法都是經驗性的,人們根據實驗經驗或直覺認識,設計出一些似是而非的工程演算法。大部分研究並沒有對 「究竟什麼是輸入單元重要性」 做出嚴謹定義和理論論證,少數研究有一定的論證,但往往也很不完善。當然,「缺乏嚴謹的定義和論證」 的問題充滿了整個人工智慧領域,只是在這兩個方向上格外突出。
當然,我們的理論分析不只適用於 14 種歸因演算法,理論上可以統一更多類似的研究。因為人力有限,這篇論文裡我們只討論 14 種演算法。
研究的真正難點在於,不同的經驗性歸因演算法往往都是搭建在不同的直覺之上的,每篇論文都僅僅努力從各自的角度「自圓其說」 ,分別基於不同的直覺或角度來設計歸因演算法,而缺少一套規範的數學語言來統一描述各種演算法的本質。
在講數學以前,本文先從直覺層面簡單回顧先前的演算法。
1. 基於梯度的歸因演算法。 這一類演算法普遍認為,神經網路的輸出對每個輸入單元的梯度可以反映輸入單元的重要性。例如,Gradient*Input 演算法將輸入單元的重要性建模為梯度與輸入單元值的逐元素乘積。考慮到梯度僅能反映輸入單元的局部重要性,Smooth Gradients 和Integrated Gradients 演算法將重要性建模為平均梯度與輸入單元值的逐元素乘積,其中這兩種方法中的平均梯度分別指輸入樣本鄰域內梯度的平均值或輸入樣本到基準點(baseline point)間線性內插點的梯度平均值。類似地,Grad-CAM 演算法採用網路輸出對每個 channel 中所有特徵梯度的平均值,來計算重要性分數。進一步,Expected Gradients 演算法認為,選擇單一基準點往往會導致有偏的歸因結果,從而提出將重要性建模為不同基準點下 Integrated Gradients 歸因結果的期望。
2. 基於逐層反向傳播的歸因演算法。 深度神經網路往往極為複雜,而每一層神經網路的結構相對簡單(例如深層特徵通常是淺層特徵的線性加和非線性活化函數),便於分析淺層特徵對深層特徵的重要性。因此,這類演算法透過估計中層特徵的重要性,並將這些重要性逐層傳播直到輸入層,得到輸入單元的重要性。這一類演算法包括 LRP-epsilon, LRP-alphabeta, Deep Taylor, DeepLIFT Rescale, DeepLIFT RevealCancel, DeepShap 等。不同反向傳播演算法間的根本差異在於,他們採用了不同的重要性逐層傳播規則。
3. 基於遮蔽的歸因演算法。 這類演算法根據遮蔽某一輸入單元對模型輸出的影響,來推論此輸入單元的重要性。例如,Occlusion-1(Occlusion-patch)演算法將第 i 個像素(像素區塊)的重要性建模為其它像素未被遮蔽時,像素 i 未遮蔽和遮蔽兩種情況下的輸出改變量。 Shapley value 演算法則綜合考慮了其它像素的所有可能遮擋情況,並將重要性建模為不同遮擋情況下像素 i 對應輸出改變量的平均值。研究已證明,Shapley value 是唯一滿足 linearity, dummy, symmetry, efficiency 公理的歸因演算法。
#在深入研究多種經驗歸因演算法後,我們不禁思考一個問題:在數學層面上,神經網路的歸因究竟在解決什麼問題?在眾多經驗歸因演算法的背後,是否蘊含某種統一的數學建模與典範?為此,我們嘗試從歸因的定義出發,並著眼於上述問題。歸因,是指每個輸入單元對神經網路輸出的重要性分數 / 貢獻。那麼,解決上述問題的關鍵在於,(1)在數學層面上建模「輸入單元對網路輸出的影響機制」,(2)解釋眾多經驗性歸因演算法是如何利用該影響機制,來設計重要性歸因公式。
針對第一個關鍵點,我們研究發現:每個輸入單元往往透過兩種方式影響神經網路的輸出。一方面,某一個輸入單元無需依賴其他輸入單元,可獨立作用並影響網路輸出,這類影響稱為 「獨立效應」。另一方面,一個輸入單元需要透過與其他輸入單元共同協作,形成某種模式,進而對網路輸出產生影響,這類影響稱為 「交互效應」。我們理論證明了,神經網路的輸出可以嚴謹解構為不同輸入變數的獨立效應,以及不同集合內輸入變數間的交互效應。
其中, 表示第i 個輸入單元的獨立效應,
表示第i 個輸入單元的獨立效應, ##表示集合S 內多個輸入單元間的交互效應。 針對第二個關鍵點,我們探究發現,所有14 種現有經驗性歸因演算法的內在機理,都可以表示對上述獨立效用和交互效用的一種分配,而不同歸因演算法以不同的比例來分配神經網路輸入單元的獨立效用和交互效用。具體地,令
##表示集合S 內多個輸入單元間的交互效應。 針對第二個關鍵點,我們探究發現,所有14 種現有經驗性歸因演算法的內在機理,都可以表示對上述獨立效用和交互效用的一種分配,而不同歸因演算法以不同的比例來分配神經網路輸入單元的獨立效用和交互效用。具體地,令 #表示第i 個輸入單元的歸因分數。我們嚴格證明了,所有14 種經驗性歸因演算法得到的,都可以統一表示為下列數學範式(即獨立效用和交互效用的加權和):
#表示第i 個輸入單元的歸因分數。我們嚴格證明了,所有14 種經驗性歸因演算法得到的,都可以統一表示為下列數學範式(即獨立效用和交互效用的加權和):

#其中, 反映了將第j 個輸入單元的獨立效果分配給第i 個輸入單元的比例,
反映了將第j 個輸入單元的獨立效果分配給第i 個輸入單元的比例, #表示將集合S 內多個輸入單元間的交互效應分配給第i 個輸入單元的比例。眾多歸因演算法的 「根本差異」 在於,不同歸因演算法對應著不同的分配比例
#表示將集合S 內多個輸入單元間的交互效應分配給第i 個輸入單元的比例。眾多歸因演算法的 「根本差異」 在於,不同歸因演算法對應著不同的分配比例  #。
#。
表 1 展示了十四種不同的歸因演算法分別是如何分配獨立效應與交互效應。

#圖表1. 十四種歸因演算法皆可寫成獨立效應與交互效應加權和的數學範式。其中 分別表示泰勒獨立效應與泰勒互動效應,滿足#
分別表示泰勒獨立效應與泰勒互動效應,滿足#
 ,是獨立效應
,是獨立效應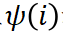 和
和 交互作用的細化。
交互作用的細化。















##########評估歸因演算法可靠度的三大準則### ######在歸因解釋研究中,由於無從獲得/ 標註神經網路歸因解釋的真實值,人們無法從實證角度評估某一個歸因解釋演算法的可靠性。 「缺乏對歸因解釋演算法可靠性的客觀評價標準」 這個根本缺陷,引發了學界對歸因解釋研究領域的廣泛批評與質疑。 ############而本研究中對歸因演算法公共機制的揭示,使我們能在同一理論架構下,公平地評估和比較不同歸因演算法的可靠性。具體地,我們提出了以下三個評估準則,以評估某一個歸因演算法是否公平合理地分配獨立效應和交互效應。 ######
(1)準則一:分配過程中涵蓋所有獨立效應與交互效應。當我們將神經網路輸出解構為獨立效應與交互效應後,可靠的歸因演算法在分配過程中應盡可能涵蓋所有的獨立效應與交互效應。例如,對I'm not happy 句子的歸因中,應涵蓋三個單字I'm, not, happy 的所有獨立效應,同時涵蓋J (I'm, not), J (I'm, happy) , J (not, happy), J (I'm, not, happy) 等所有可能的交互效應。
(2)準則二:避免將獨立效應與交互作用分配給無關的輸入單元。第 i 個輸入單元的獨立效應,只應分配給第 i 個輸入單元,而不應分配給其它輸入單元。類似地,集合 S 內輸入單元間的交互效應,只應分配給集合 S 內的輸入單元,而不應分配給集合 S 以外的輸入單元(未參與交互)。例如,not 和 happy 之間的交互效應,不應分配給單字 I’m。
(3)準則三:完全指派。每個獨立效應(交互效應)應完全分配給對應的輸入單元。換句話說,某一個獨立效應(交互效應)分配給所有對應輸入單元的歸因值,加起來應恰好等於該獨立效應(交互效應)的值。例如,交互效應J (not, happy) 會分配一部分效應 (not, happy) 給單字not,同時分配一部分效應
(not, happy) 給單字not,同時分配一部分效應  (not, happy)給單字happy。那麼,分配比例應滿足
(not, happy)給單字happy。那麼,分配比例應滿足 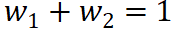 。
。
接著,我們採用這三個評估準則,評估了上述 14 種不同歸因演算法(如表 2 所示)。我們發現,Integrated Gradients, Expected Gradients, Shapley value, Deep Shap, DeepLIFT Rescale, DeepLIFT RevealCancel 這些演算法符合所有的可靠性準則。

表2. 總結14 個不同歸因演算法是否滿足三個可靠性評估準則。
本文作者鄧輝琦,是中山大學應用數學專業的博士,博士期間曾在香港浸會大學和德州農工大學計算機系訪問學習,現於張拳石老師團隊進行博士後研究。研究方向主要為可信 / 可解釋機器學習,包括解釋深度神經網路的歸因重要性、解釋神經網路的表達能力等。
鄧輝琦前期做了很多工作。張老師只是在初期工作結束以後,幫她重新整理了一遍理論,讓證明方式和體系更順暢一些。鄧輝琦畢業前論文不是很多,21 年末來張老師這邊以後,在博弈交互的體系下,一年多做了三個工作,包括(1)發現並理論解釋了神經網絡普遍存在的表徵瓶頸,即證明神經網路較不善於建模中等複雜度的交互表徵。這項工作有幸被選為 ICLR 2022 oral 論文,審稿得分排名前五(得分 8 8 8 10)。 (2)理論證明了貝葉斯網路的概念表徵趨勢,為解釋貝葉斯網路的分類效能、泛化能力和對抗穩健性提供了新的視角。 (3)從理論層面解釋了神經網路在訓練過程中對不同複雜度互動概念的學習能力。
以上是理解並統一14種歸因演算法,讓神經網路具有可解釋性的詳細內容。更多資訊請關注PHP中文網其他相關文章!




