Python怎麼呼叫實作最小平方法-Python教學-PHP中文網

所謂線性最小平方法，可以理解為是解方程式的延續，差異在於，當未知量遠小於方程式數的時候，將會得到一個無解的問題。最小平方法的實質，是保證誤差最小的情況下對未知數進行賦值。

最小平方法是非常經典的演算法，而且這個名字我們在高中的時候就已經接觸了，屬於極為常用的演算法。先前曾經寫過線性最小平方法的原理，並用Python實現：最小二乘法及其Python實現；以及scipy中非線性最小二乘法的調用方式：非線性最小二乘法（文末補充內容）；還有稀疏矩陣的最小平方法：稀疏矩陣最小平方法。

下面講對numpy和scipy中實現的線性最小平方法進行說明，並比較二者的速度。

numpy實作

numpy中便實現了最小二乘法，即lstsq(a,b)用於求解類似於a@x=b中的x，其中，a為M× N的矩陣；則當b為M行的向量時，剛好相當於解線性方程組。對於Ax=b這樣的方程組，如果A是滿秩仿真，那麼可以表示為x=A⁻¹b，否則可以表示為x=(A^TA)⁻¹A^Tb。

當b為M×K的矩陣時，則對每一列，都會計算一組x。

其回傳值共有4個，分別是擬合得到的x、擬合誤差、矩陣a的秩、以及矩陣a的單值形式。

import numpy as np
np.random.seed(42)
M = np.random.rand(4,4)
x = np.arange(4)
y = M@x
xhat = np.linalg.lstsq(M,y)
print(xhat[0])
#[0. 1. 2. 3.]

登入後複製

scipy封裝

scipy.linalg同樣提供了最小平方法函數，函數名稱同樣是lstsq，其參數列表為

lstsq(a, b, cond=None, overwrite_a=False, overwrite_b=False, check_finite=True, lapack_driver=None)

登入後複製

其中a, b即Ax= b，二者皆提供可覆寫開關，設為True可以節省運行時間，此外，函數也支援有限性檢查，這是linalg中許多函數都具備的選項。其傳回值與numpy中的最小平方法函數相同。

cond為浮點型參數，表示奇異值閾值，當奇異值小於cond時將捨棄。

lapack_driver為字串選項，表示選用何種LAPACK中的演算法引擎，可選'gelsd', 'gelsy', 'gelss'。

import scipy.linalg as sl
xhat1 = sl.lstsq(M, y)
print(xhat1[0])
# [0. 1. 2. 3.]

登入後複製

速度對比

最後，對著兩組最小二乘函數做一個速度上的對比

from timeit import timeit
N = 100
A = np.random.rand(N,N)
b = np.arange(N)

timeit(lambda:np.linalg.lstsq(A, b), number=10)
# 0.015487500000745058
timeit(lambda:sl.lstsq(A, b), number=10)
# 0.011151800004881807

登入後複製

這一次，二者並沒有拉開太大的差距，即使將矩陣維度放大到500，二者也是半斤八兩。

N = 500
A = np.random.rand(N,N)
b = np.arange(N)

timeit(lambda:np.linalg.lstsq(A, b), number=10)
0.389679799991427
timeit(lambda:sl.lstsq(A, b), number=10)
0.35642060000100173

登入後複製

補充

Python呼叫非線性最小平方法

簡介與建構子

在在scipy中，非線性最小二乘法的目的是找到一組函數，使得誤差函數的平方和最小，可以表示為如下公式

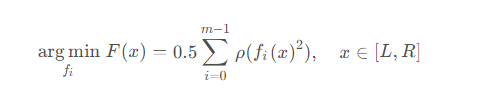
Python怎麼呼叫實作最小平方法

其中ρ表示損失函數，可以理解為對f_i(x)的一次預處理。

scipy.optimize中封裝了非線性最小二乘法函數least_squares，其定義為

least_squares(fun, x0, jac, bounds, method, ftol, xtol, gtol, x_scale, f_scale, loss, jac_sparsity, max_nfev, verbose, args, kwargs)

登入後複製

其中，func和x0為必選參數，func為待求解函數，x0為函數輸入的初值，這兩者無預設值，為必須輸入的參數。

bound為求解區間，預設(−∞,∞)，verbose為1時，會有終止輸出，為2時會print更多的運算過程中的資訊。另外下面幾個參數用來控制誤差，比較簡單。

##f_scale1.0殘差邊際值

loss为损失函数，就是上面公式中的ρ \rhoρ，默认为linear，可选值包括

Python怎麼呼叫實作最小平方法

迭代策略

上面的公式仅给出了算法的目的，但并未暴露其细节。关于如何找到最小值，则需要确定搜索最小值的方法，method为最小值搜索的方案，共有三种选项，默认为trf

trf：即Trust Region Reflective，信赖域反射算法
dogbox：信赖域狗腿算法
lm：Levenberg-Marquardt算法

这三种方法都是信赖域方法的延申，信赖域的优化思想其实就是从单点的迭代变成了区间的迭代，由于本文的目的是介绍scipy中所封装好的非线性最小二乘函数，故而仅对其原理做简略的介绍。

Python怎麼呼叫實作最小平方法

其中r为置信半径，假设在这个邻域内，目标函数可以近似为线性或二次函数，则可通过二次模型得到区间中的极小值点s_k。然后以这个极小值点为中心，继续优化信赖域所对应的区间。

Python怎麼呼叫實作最小平方法

雅可比矩阵

在了解了信赖域方法之后，就会明白雅可比矩阵在数值求解时的重要作用，而如何计算雅可比矩阵，则是接下来需要考虑的问题。jac参数为计算雅可比矩阵的方法，主要提供了三种方案，分别是基于两点的2-point；基于三点的3-point；以及基于复数步长的cs。一般来说，三点的精度高于两点，但速度也慢一倍。

此外，可以输入自定义函数来计算雅可比矩阵。

测试

最后，测试一下非线性最小二乘法

import numpy as np
from scipy.optimize import least_squares

def test(xs):
    _sum = 0.0
    for i in range(len(xs)):
        _sum = _sum + (1-np.cos((xs[i]*i)/5)*(i+1))
    return _sum

x0 = np.random.rand(5)
ret = least_squares(test, x0)
msg = f"最小值" + ", ".join([f"{x:.4f}" for x in ret.x])
msg += f"\nf(x)={ret.fun[0]:.4f}"
print(msg)
&#39;&#39;&#39;
最小值0.9557, 0.5371, 1.5714, 1.6931, 5.2294
f(x)=0.0000
&#39;&#39;&#39;

登入後複製

以上是Python怎麼呼叫實作最小平方法的詳細內容。更多資訊請關注PHP中文網其他相關文章！

相關標籤：

python

來源：yisu.com

上一篇：Python變數的定義和運算子如何使用下一篇：Python 實作堆疊的幾種方式及其優劣

本網站聲明

本文內容由網友自願投稿，版權歸原作者所有。本站不承擔相應的法律責任。如發現涉嫌抄襲或侵權的內容，請聯絡admin@php.cn

作者最新文章