python提供了多種卷積方案,相較之下,定義在ndimage中的捲積函數,在功能上比numpy和signal中的捲積要稍微複雜一些,這點僅從輸入參數的多少就可略窺一二
numpy.convolve(a, v, mode='full') scipy.ndimage.convolve1d(input, weights, axis=-1, output=None, mode='reflect', cval=0.0, origin=0) scipy.signal.convolve(in1, in2, mode='full', method='auto') scipy.ndimage.convolve(input, weights, output=None, mode='reflect', cval=0.0, origin=0)
前兩者為1維卷積函數,且ndimage可對多維數組沿著單一座標軸進行卷積操作,後兩者為多維卷積。
numpy和signal中的捲積函數,其mode都有三種,用以調節卷積後的邊緣特性,如果輸入的兩個卷積物件的維度分別是N NN和M MM,則這三種模式的輸出結果為
full: 輸出維度N M − 1 N M-1N M−1,其最後一點的訊號完全不交疊,故而邊緣效應明顯。
same:輸出維度max ( M , N ) \max(M,N)max(M,N),邊緣效應仍可見
valid:輸出維度∣ M − N ∣ |M-N|∣M−N∣,只回傳完全交疊的區域,相當於把存在邊緣效應的點都率除掉了
ndimage中的convolve針對邊緣效應,對影像進行擴展,而其mode決定的就是擴充之後的填滿格式,設待濾波陣列為a b c d,則在不同的模式下,對邊緣進行如下填入
| 資料 | #右側填充 | ||
|---|---|---|---|
reflect | d c b aa b c d | d c b a | |
constant | #k k k k a b c d | k k k k | |
#nearest | #a b c d | d d d d | |
| a b c d | ##c b a||
|
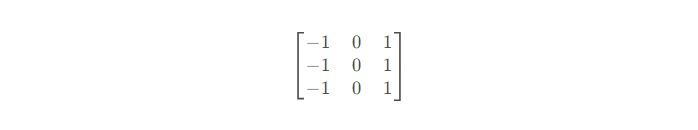
import numpy as np import scipy.signal as ss import scipy.ndimage as sn from timeit import timeit A = np.random.rand(1000,1000) B = np.random.rand(5,5) timeit(lambda : ss.convolve(A, B), number=10) # 0.418 timeit(lambda : sn.convolve(A, B), number=10) # 0.126
A = np.random.rand(10000) B = np.random.rand(15) timeit(lambda : np.convolve(A, B), number=1000) # 0.15256029999727616 timeit(lambda : ss.convolve(A, B), number=1000) # 0.1231262000001152 timeit(lambda : sn.convolve(A, B), number=1000) # 0.09218210000108229 timeit(lambda : sn.convolve1d(A, B), number=1000) # 0.03915820000111125
from scipy.misc import ascent import matplotlib.pyplot as plt img = ascent() temp = np.zeros([3,3]) temp[:,0] = -1 temp[:,2] = 1 edge = sn.convolve(img, temp) fig = plt.figure() ax = fig.add_subplot(121) ax.imshow(img) ax = fig.add_subplot(122) ax.imshow(edge) plt.show()
以上是Python卷積函數怎麼用的詳細內容。更多資訊請關注PHP中文網其他相關文章!




