Python基本形態學濾波怎麼實現

最基礎的形態學操作有四個，分別是腐蝕、膨脹、開計算和閉計算，`scipy.ndimage分別實現了二值數組和灰度數組的這四種運算

binary_closing##binary_closinggrey_closing閉(先膨脹後腐蝕)binary_openinggrey_opening

二值	灰階
#binary_erosion	grey_erosion	腐蝕
binary_dilation

開(先腐蝕後膨脹)

二值形態學

所謂腐蝕，用數學符號表示為

##其中B

ij

表示當B BB的原點在(i,j)處時，B中所有為1的值的集合。

這個式子的意思是，用結構B腐蝕A，當B的原點平移到圖像A的像元(i,j)時，若B完全被二者的重疊區域所包圍，則賦值為1，否則賦值為0。當B中某個元素為1時，若A中對應位置也是1，則(i,j)處的值為1，這是較直觀的例子。

膨脹則與之相反，可表示為

換言之，只要B和A的重疊區域不是空集，那麼(i,j)點就置為1。

舉例如下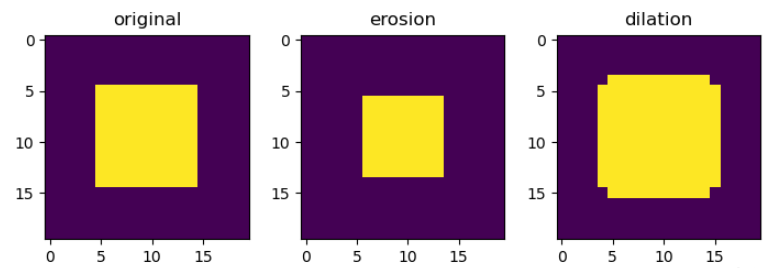

import numpy as np
import matplotlib.pyplot as plt
import scipy.ndimage as sn

x = np.zeros([20,20])
x[5:15, 5:15] = 1
x_ero = sn.binary_erosion(x)
x_dil = sn.binary_dilation(x)

fig = plt.figure()
ax = fig.add_subplot(1,3,1)
ax.imshow(x)
plt.title("original")
ax = fig.add_subplot(1,3,2)
ax.imshow(x_ero)
plt.title("erosion")
ax = fig.add_subplot(1,3,3)
ax.imshow(x_dil)
plt.title("dilation")
plt.show()

效果如下

#開運算是先腐蝕後膨脹；閉運算是先膨脹後腐蝕，範例如下

x = np.zeros([20,20])
x[5:15, 5:15] = 1
x[10:12,10:12] = 0
x[2:4, 2:4] = 1

x_open = sn.binary_opening(x)
x_close = sn.binary_closing(x)

fig = plt.figure()
ax = fig.add_subplot(1,3,1)
ax.imshow(x)
plt.title("original")
ax = fig.add_subplot(1,3,2)
ax.imshow(x_open)
plt.title("opening")
ax = fig.add_subplot(1,3,3)
ax.imshow(x_close)
plt.title("closing")
plt.show()

效果如下，可見開運算會移除孤立的1，閉運算會移除孤立的0。

灰階形態學

灰階影像的腐蝕、膨脹以及開閉運算，是其二值形勢下的一個擴展，採用了類似卷積的邏輯，下面直接從scipy中調取樓梯圖片，並依序做腐蝕、膨脹以及開閉操作。

from scipy.misc import ascent
img = ascent()

funcs = {
    "original": lambda x, tmp:x,
    "erosion" : sn.grey_erosion,
    "dilation" : sn.grey_dilation,
    "opening" : sn.grey_opening,
    "closing" : sn.grey_closing
}

fig = plt.figure()
for i, key in enumerate(funcs):
    ax = fig.add_subplot(2,3,i+1)
    plt.imshow(funcs[key](img, (10,10)), cmap=plt.cm.gray)
    plt.title(key)

plt.show()

參數列表

• 二值函數和灰階函數的參數並不相同，下面以closing運算為例，二值和灰階函數的所有參數，除了輸入input之外，二者共有的參數有

• structure 為數組類型，表示建構元素，可以理解為是卷積模板

• output 與輸入相同維度的數組，可以存下結果

orgin 過濾器設置，預設為0

##二值形態學濾波的其他參數如下

binary_closing(input, iterations=1, mask=None, border_value=0, brute_force=False)

• 其中

• iterations 執行次數

• mask 掩模數組，為bool類型的數組，對應False的位置將不會改變

• border_value 邊緣處的值

brute_force 如果為False，則只有上次迭代中發生變化的值才會更新

• grey_closing(input, size=None, footprint=None, mode='reflect', cval=0.0)

• size 為濾波模板

##mode 可選reflect,constant, nearest,mirror, wrap，邊緣填滿方式
cval 邊緣填滿值#######

以上是Python基本形態學濾波怎麼實現的詳細內容。更多資訊請關注PHP中文網其他相關文章！