python如何實作決策樹分類演算法-Python教學-PHP中文網

編號	#年齡				#信用評級
	#01		高	不穩定	較差
	#02		高	不穩定	好
	#03	30-40	高	不穩定	較差
	#04	>40	中	不穩定	較差
	#05	>40	低	穩定	較差
	06	#> 40	低	穩定	好
	#07	30- 40	低	穩定	好

					#
穩定	較差	#是		10	>40
穩定	較差	#是		11
穩定	好	#是		12	30-40
不穩定	好	#是		13	30-40
穩定	較差	是		14	>40

不穩定######好######否######################################

策樹分類演算法

1、建立資料集

為了方便處理，對類比資料依下列規則轉換為數值型清單資料：

年齡：< ;30賦值為0；30-40賦值為1；>40賦值為2

收入：低為0；中為1；高為2

工作性質：不穩定為0；穩定為1

信用評級：差為0；好為1

#创建数据集
def createdataset():
    dataSet=[[0,2,0,0,&#39;N&#39;],
            [0,2,0,1,&#39;N&#39;],
            [1,2,0,0,&#39;Y&#39;],
            [2,1,0,0,&#39;Y&#39;],
            [2,0,1,0,&#39;Y&#39;],
            [2,0,1,1,&#39;N&#39;],
            [1,0,1,1,&#39;Y&#39;],
            [0,1,0,0,&#39;N&#39;],
            [0,0,1,0,&#39;Y&#39;],
            [2,1,1,0,&#39;Y&#39;],
            [0,1,1,1,&#39;Y&#39;],
            [1,1,0,1,&#39;Y&#39;],
            [1,2,1,0,&#39;Y&#39;],
            [2,1,0,1,&#39;N&#39;],]
    labels=[&#39;age&#39;,&#39;income&#39;,&#39;job&#39;,&#39;credit&#39;]
    return dataSet,labels

登入後複製

呼叫函數，可取得資料：

ds1,lab = createdataset()
print(ds1)
print(lab)

登入後複製

[[0, 2 , 0, 0, ‘N’], [0, 2, 0, 1, ‘N’], [1, 2, 0, 0, ‘Y’], [2, 1, 0, 0, ‘Y’], [2, 0, 1, 0, ‘Y’], [2, 0, 1, 1, ‘N’], [1, 0, 1, 1, ‘Y’] , [0, 1, 0, 0, ‘N’], [0, 0, 1, 0, ‘Y’], [2, 1, 1, 0, ‘Y’], [0, 1 , 1, 1, ‘Y’], [1, 1, 0, 1, ‘Y’], [1, 2, 1, 0, ‘Y’], [2, 1, 0, 1, ‘N’]]
[‘age’, ‘income’, ‘job’, ‘credit’]

#2、資料集資訊熵

# #資訊熵也稱為香農熵，是隨機變數的期望。度量資訊的不確定程度。訊息的熵越大，訊息就越不容易搞清楚。處理資訊就是為了把資訊搞清楚，就是熵減少的過程。

def calcShannonEnt(dataSet):
    numEntries = len(dataSet)
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        
        labelCounts[currentLabel] += 1            
        
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob*log(prob,2)
    
    return shannonEnt

登入後複製

樣本資料資訊熵：

shan = calcShannonEnt(ds1)
print(shan)

登入後複製

0.9402859586706309

3、資訊增益

資訊增益：用於度量屬性A降低樣本集合X熵的貢獻大小。資訊增益越大，越適於對X分類。

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0])-1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0;bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntroy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prop = len(subDataSet)/float(len(dataSet))
            newEntroy += prop * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntroy
        if(infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i    
    return bestFeature

登入後複製

以上程式碼實現了基於資訊熵增益的ID3決策樹學習演算法。其核心邏輯原理為：依序選取屬性集中的每一個屬性，將樣本集依此屬性的取值分割為若干個子集；對這些子集計算資訊熵，其與樣本的資訊熵的差，即為依照此屬性分割的資訊熵增益；找出所有增益中最大的那一個對應的屬性，就是用來分割樣本集的屬性。

計算樣本最佳的分割樣本屬性，結果顯示為第0列，即age屬性：

col = chooseBestFeatureToSplit(ds1)
col

登入後複製

0

4、建構決策樹

def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys():classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classList.iteritems(),key=operator.itemgetter(1),reverse=True)#利用operator操作键值排序字典
    return sortedClassCount[0][0]

#创建树的函数    
def createTree(dataSet,labels):
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
        
    return myTree

登入後複製

majorityCnt函數用來處理情況：當最終的理想決策樹應該沿著決策分支到達最底端時，所有的樣本應該都是相同的分類結果。但真實樣本中難免會出現所有屬性一致但分類結果不一樣的情況，此時majorityCnt將這類樣本的分類標籤都調整為出現次數最多的那一個分類結果。

createTree是核心任務函數，它對所有的屬性依序呼叫ID3資訊熵增益演算法進行計算處理，最終產生決策樹。

5、實例化建構決策樹

利用樣本資料建構決策樹：

Tree = createTree(ds1, lab)
print("样本数据决策树：")
print(Tree)

登入後複製

樣本資料決策樹：
{‘age’: {0: {‘job’: {0: ‘N’, 1: ‘Y’}},
1: ‘Y’,
2: {‘credit’: {0: ‘Y’, 1: ‘N’}}}}

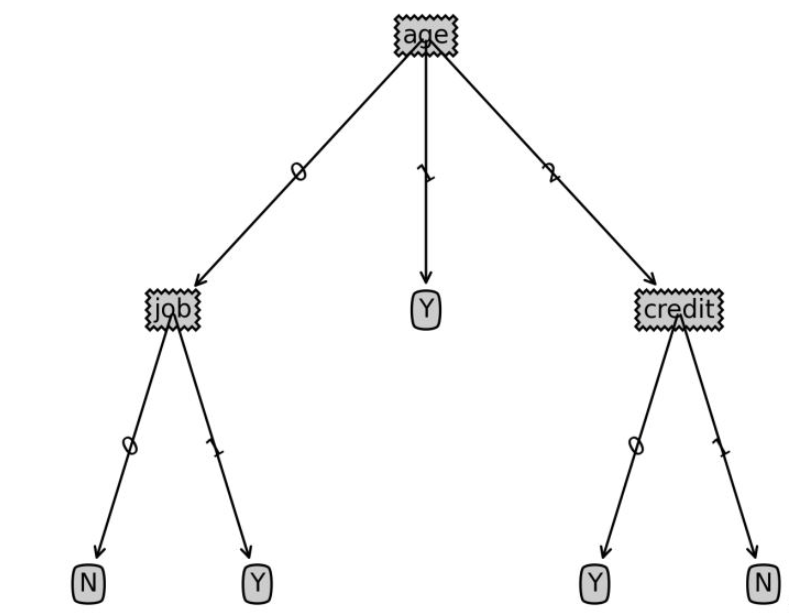
python如何實作決策樹分類演算法

#6、測試樣本分類

##給予一個新的用戶訊息，判斷ta是否購買某一產品：

年齡#收入範圍工作性質#信用評級<30低#穩定好<30高不穩定好

def classify(inputtree,featlabels,testvec):
    firststr = list(inputtree.keys())[0]
    seconddict = inputtree[firststr]
    featindex = featlabels.index(firststr)
    for key in seconddict.keys():
        if testvec[featindex]==key:
            if type(seconddict[key]).__name__==&#39;dict&#39;:
                classlabel=classify(seconddict[key],featlabels,testvec)
            else:
                classlabel=seconddict[key]
    return classlabel

登入後複製

labels=[&#39;age&#39;,&#39;income&#39;,&#39;job&#39;,&#39;credit&#39;]
tsvec=[0,0,1,1]
print(&#39;result:&#39;,classify(Tree,labels,tsvec))
tsvec1=[0,2,0,1]
print(&#39;result1:&#39;,classify(Tree,labels,tsvec1))

登入後複製

result: Y
result1: N

後置資訊：繪製決策樹程式碼

#以下程式碼用於繪製決策樹圖形，非決策樹演算法重點，有興趣可參考學習

import matplotlib.pyplot as plt

decisionNode = dict(box, fc="0.8")
leafNode = dict(box, fc="0.8")
arrow_args = dict(arrow)

#获取叶节点的数目
def getNumLeafs(myTree):
    numLeafs = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__==&#39;dict&#39;:#测试节点的数据是否为字典，以此判断是否为叶节点
            numLeafs += getNumLeafs(secondDict[key])
        else:   numLeafs +=1
    return numLeafs

#获取树的层数
def getTreeDepth(myTree):
    maxDepth = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__==&#39;dict&#39;:#测试节点的数据是否为字典，以此判断是否为叶节点
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:   thisDepth = 1
        if thisDepth > maxDepth: maxDepth = thisDepth
    return maxDepth

#绘制节点
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt, xy=parentPt,  xycoords=&#39;axes fraction&#39;,
             xytext=centerPt, textcoords=&#39;axes fraction&#39;,
             va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )

#绘制连接线  
def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
    yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)

#绘制树结构  
def plotTree(myTree, parentPt, nodeTxt):#if the first key tells you what feat was split on
    numLeafs = getNumLeafs(myTree)  #this determines the x width of this tree
    depth = getTreeDepth(myTree)
    firstStr = list(myTree.keys())[0]     #the text label for this node should be this
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
    plotMidText(cntrPt, parentPt, nodeTxt)
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[key]).__name__==&#39;dict&#39;:#test to see if the nodes are dictonaires, if not they are leaf nodes   
            plotTree(secondDict[key],cntrPt,str(key))        #recursion
        else:   #it&#39;s a leaf node print the leaf node
            plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD

#创建决策树图形    
def createPlot(inTree):
    fig = plt.figure(1, facecolor=&#39;white&#39;)
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)    #no ticks
    #createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses 
    plotTree.totalW = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;
    plotTree(inTree, (0.5,1.0), &#39;&#39;)
    plt.savefig(&#39;决策树.png&#39;,dpi=300,bbox_inches=&#39;tight&#39;)
    plt.show()

登入後複製

以上是python如何實作決策樹分類演算法的詳細內容。更多資訊請關注PHP中文網其他相關文章！

本網站聲明

本文內容由網友自願投稿，版權歸原作者所有。本站不承擔相應的法律責任。如發現涉嫌抄襲或侵權的內容，請聯絡admin@php.cn