再見 Go 面試官：GMP 模型，為什麼要有 P？

今天的主角，是Go 面試的萬能題GMP 模型的延伸題（疑問），那就是」GMP 模型，為什麼要有P ？出來，那麼麻煩，為的是什麼，是要解決什麼問題嗎

？ 「

這篇文章煎魚就帶你一同探索，GM、GMP 模型的變遷是因為什麼原因。

GM 模型

在 Go1.1 之前 Go 的調度模型其實就是 GM 模型，也就是沒有 P。

今天帶大家一起回顧過去的設計。

解密Go1.0 原始碼

#我們了解一個東西的方法之一就是看源碼，和煎魚一起看看Go1.0.1的調度器原始碼的核心關鍵步驟：

static void
schedule(G *gp)
{
 ...
 schedlock();
 if(gp != nil) {
  ...
  switch(gp->status){
  case Grunnable:
  case Gdead:
   // Shouldn't have been running!
   runtime·throw("bad gp->status in sched");
  case Grunning:
   gp->status = Grunnable;
   gput(gp);
   break;
  }

 gp = nextgandunlock();
 gp->readyonstop = 0;
 gp->status = Grunning;
 m->curg = gp;
 gp->m = m;
 ...
 runtime·gogo(&gp->sched, 0);
}

• 呼叫 schedlock 方法來取得全域鎖定。
• 取得全域鎖定成功後，將目前 Goroutine 狀態從 Running（正在被調度） 狀態修改為 Runnable（可以被排程）狀態。
• 呼叫 gput 方法來保存目前 Goroutine 的運行狀態等信息，以便於後續的使用。
• 呼叫 nextgandunlock 方法來尋找下一個可運行 Goroutine，並且釋放全域鎖定給其他調度使用。
• 取得到下一個待運行的 Goroutine 後，將其運行狀態修改為 Running。
• 呼叫 runtime·gogo 方法，將剛剛所取得的下一個待執行的 Goroutine 運行起來，進入下一輪調度。

思考GM 模型

透過對Go1.0.1 的調度器原始碼剖析，我們可以發現一個比較有趣的點。那就是調度器本身（schedule 方法），在正常流程下，是不會回傳的，也就是不會結束主流程。

G-M模型簡圖

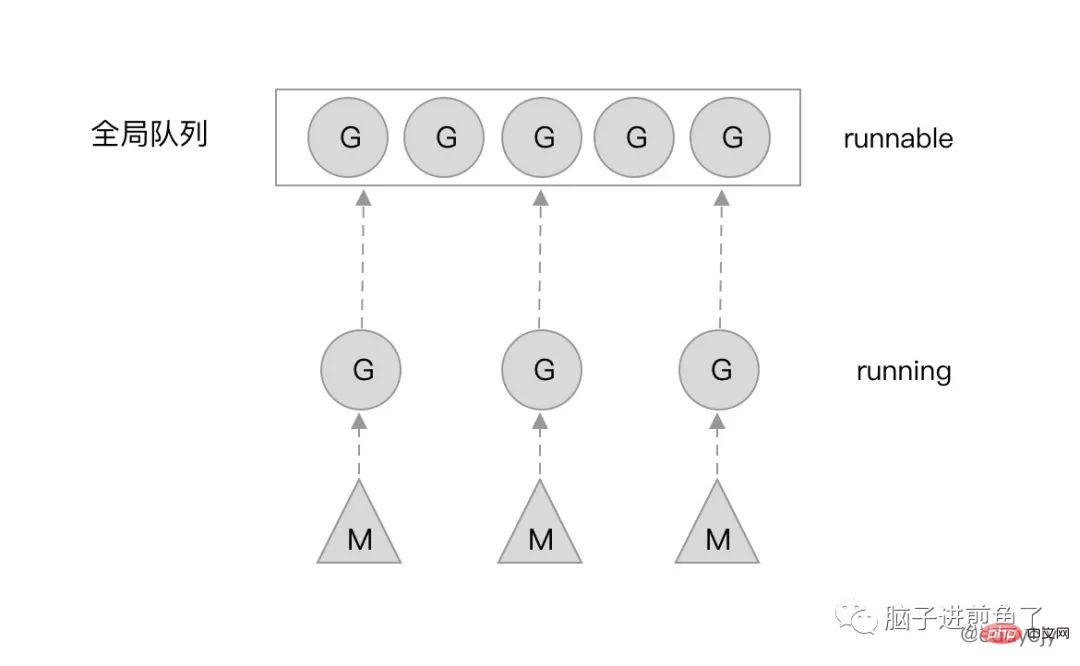
他會不斷地運行調度流程，GoroutineA 完成了，就開始尋找GoroutineB，尋找到B 了，就把已經完成的A 的調度權交給B，讓GoroutineB 開始被調度，也就是運作。

當然了，也有被正在阻塞（Blocked）的 G。假設 G 正在做一些系統、網路調用，那麼就會導致 G 停滯。這時候 M（系統執行緒）就會被會重新放入核心佇列中，等待新的一輪喚醒。

GM 模型的缺點

這麼表面的看起來，GM 模型似乎牢不可破，毫無缺陷。但為什麼要改呢？

在2012 年時Dmitry Vyukov 發表了文章《Scalable Go Scheduler Design Doc》，目前也依然是各大研究Go 調度器文章的主要對象，其在文章內講述了整體的原因和考慮，下述內容將引用該文章。

目前（代指 Go1.0 的 GM 模型）的 Goroutine 調度器限制了用 Go 編寫的並發程式的可擴展性，尤其是高吞吐量伺服器和平行計算程式。

實作有以下的問題：

• 存在單一的全域mutex（Sched.Lock）與集中狀態管理：
• mutex 需要保護所有與goroutine 相關的操作（創建、完成、重排等），導致鎖定競爭嚴重。
• Goroutine 傳遞的問題：
• #goroutine（G）交接（G.nextg）：工作者執行緒（ M's）之間會經常交接可運行的goroutine。
• 上述可能會導致延遲增加和額外的開銷。每個 M 必須能夠執行任何可運行的 G，特別是剛剛創建 G 的 M。
• 每個M 都需要做記憶體快取（M.mcache）：
• ##會導致資源消耗過大（每個mcache 可以吸收到2M 的記憶體快取和其他快取），資料局部性差。
• 頻繁的執行緒阻塞/解阻塞：
• 在存在syscalls 的情況下，執行緒經常被阻塞和解阻塞。這增加了很多額外的效能開銷。

GMP 模型

為了解決GM 模型的以上諸多問題，在Go1.1 時，Dmitry Vyukov 在GM 模型的基礎上，新增了一個P（Processor）元件。並且實作了 Work Stealing 演算法來解決一些新產生的問題。

GMP 模型，在上一篇文章《Go 群友提問：Goroutine 數量控制在多少合適，會影響 GC 和調度？ 》中已經講解過了。

覺得不錯的朋友可以關註一下，這裡就不再複述了。

帶來什麼改變

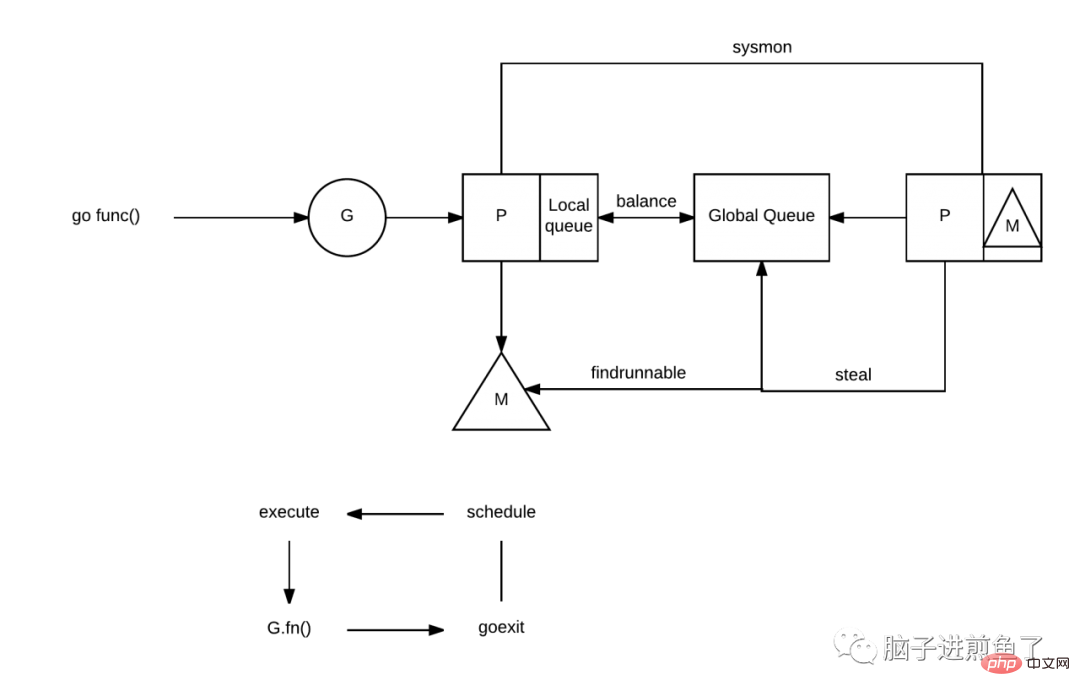
加上了 P 之後會帶來什麼改變呢？我們再更顯式的講一下。

• 每個 P 有自己的本地佇列，大幅度的減輕了對全域佇列的直接依賴，所帶來的效果就是鎖定競爭的減少。而 GM 模型的效能開銷大頭就是鎖定競爭。

• 每個P 相對的平衡上，在GMP 模型中也實作了Work Stealing 演算法，如果P 的本機佇列為空，則會從全域佇列或其他P 的本機佇列中竊取可運行的G 來運行，減少空轉，提高了資源利用率。

為什麼要有P

#這時候就有小夥伴會疑惑了，如果是想實作本地隊列、Work Stealing 演算法，那為什麼不直接在M 上加呢，M 也照樣可以實現類似的功能。

為什麼再加多一個 P 元件？

結合 M（系統執行緒） 的定位來看，若這麼做，有以下問題。

• 一般來講，M 的數量都會多於 P。像在 Go 中，M 的數量最大限制是 10000，P 的預設數量的 CPU 核數。另外由於 M 的屬性，也就是如果有系統阻塞調用，阻塞了 M，又不夠用的情況下，M 會不斷增加。

• M 不斷增加的話，如果本地佇列掛載在 M 上，那就意味著本地佇列也會隨之增加。這顯然是不合理的，因為本地佇列的管理會變得複雜，且 Work Stealing 效能會大幅下降。

• M 被系統呼叫阻塞後，我們是期望把他既有未執行的任務分配給其他繼續運行的，而不是一阻塞就導致全部停止。

因此使用 M 是不合理的，那麼引入新的元件 P，把本地佇列關聯到 P 上，就能很好的解決這個問題。

總結

今天這篇文章結合了整個 Go 語言調度器的一些歷史情況、原因分析以及解決方案說明。

」GMP 模型，為什麼要有 P「 這個問題就像是一道系統設計了解，因為現在很多人為了應對面試，會硬背 GMP 模型，或者是泡麵式過了一遍。而理解其中真正背後的原因，才是我們要去學習的去理解。

知其然知其所以然，才可破局。

#

以上是再見 Go 面試官：GMP 模型，為什麼要有 P？的詳細內容。更多資訊請關注PHP中文網其他相關文章！