在Java中的記憶化（1D，2D和3D）動態規劃

記憶化是一種基於動態規劃的技術，用於透過確保方法不會對相同的輸入集合運行多次來改進遞歸演算法的性能，透過記錄提供的輸入的結果（儲存在數組中）。可以透過實現遞歸方法的自頂向下的方法來實現記憶化。

讓我們透過基本的斐波那契數列範例來理解這種情況。

1-D記憶化

我們將考慮一個只有一個非常量參數（只有一個參數的值改變）的遞歸演算法，因此這個方法稱為1-D記憶化。以下程式碼是用來找出斐波那契數列中第N個（所有項直到N）的。

範例

public int fibonacci(int n) {
   if (n == 0)
      return 0;
   if (n == 1)
      return 1;
   System.out.println("Calculating fibonacci number for: " + n);
   return (fibonacci(n - 1) + fibonacci(n - 2));
}

輸出

如果我們使用n=5執行上述程式碼，將會產生以下輸出。

Calculating fibonacci number for: 5
Calculating fibonacci number for: 4
Calculating fibonacci number for: 3
Calculating fibonacci number for: 2
Calculating fibonacci number for: 2
Calculating fibonacci number for: 3
Calculating fibonacci number for: 2

n=5的斐波那契值為：5

注意到對於2和3的斐波那契數被計算了多次。讓我們透過繪製上述條件n=5的遞歸樹來更好地理解。

在節點的兩個子節點將表示它所做的遞歸呼叫。可以看到F(3)和F(2)被計算了多次，可以透過在每一步之後快取結果來避免。

我們將使用一個實例變數memoize Set來快取結果。首先檢查memoize Set中是否已經存在n，如果是，則傳回該值；如果不是，則計算該值並將其新增至集合。

範例

import java.util.HashMap;
import java.util.Map;
public class TutorialPoint {
   private Map<Integer, Integer> memoizeSet = new HashMap<>(); // O(1)
   public int fibMemoize(int input) {
      if (input == 0)
         return 0;
      if (input == 1)
         return 1;
      if (this.memoizeSet.containsKey(input)) {
         System.out.println("Getting value from computed result for " + input);
         return this.memoizeSet.get(input);
      }
      int result = fibMemoize(input - 1) + fibMemoize(input - 2);
      System.out.println("Putting result in cache for " + input);
      this.memoizeSet.put(input, result);
      return result;
   }
   public int fibonacci(int n) {
      if (n == 0)
         return 0;
      if (n == 1)
         return 1;
      System.out.println("Calculating fibonacci number for: " + n);
      return (fibonacci(n - 1) + fibonacci(n - 2));
   }
   public static void main(String[] args) {
      TutorialPoint tutorialPoint = new TutorialPoint();
      System.out.println("Fibonacci value for n=5: " + tutorialPoint.fibMemoize(5));
   }
}

輸出

如果我們執行上述程式碼，將會產生以下輸出

Adding result in memoizeSet for 2
Adding result in memoizeSet for 3
Getting value from computed result for 2
Adding result in memoizeSet for 4
Getting value from computed result for 3
Adding result in memoizeSet for 5

n=5時的斐波那契值為：5

從上面可以看出，2和3的斐波那契數不會再計算。在這裡，我們引入了一個HashMap memorizes來儲存已經計算過的值，在每次斐波那契計算之前，檢查集合中是否已經計算了輸入的值，如果沒有，則將特定輸入的值加到集合中。

2-D Memorization

在上面的程式中，我們只有一個非常數參數。在下面的程式中，我們將以遞歸程式為例，該程式具有兩個參數，在每次遞歸呼叫後更改其值，並且我們將在兩個非常數參數上實現記憶化以進行最佳化。這被稱為2-D記憶化。

例如：我們將實作標準的最長公共子序列(LCS)。如果給定一組序列，則最長公共子序列問題是找到所有序列的共同子序列，該子序列的長度最大。可能的組合將有2^n個。

範例

class TP {
   static int computeMax(int a, int b) {
      return (a > b) ? a : b;
   }
   static int longestComSs(String X, String Y, int m, int n) {
      if (m == 0 || n == 0)
         return 0;
      if (X.charAt(m - 1) == Y.charAt(n - 1))
         return 1 + longestComSs(X, Y, m - 1, n - 1);
      else
         return computeMax(longestComSs(X, Y, m, n - 1), longestComSs(X, Y, m - 1, n));
   }
   public static void main(String[] args) {
      String word_1 = "AGGTAB";
      String word_2 = "GXTXAYB";
      System.out.print("Length of LCS is " + longestComSs(word_1, word_2, word_1.length(),word_2.length()));
   }
}

輸出

如果我們執行上述程式碼，將會產生以下輸出

Length of LCS is 4

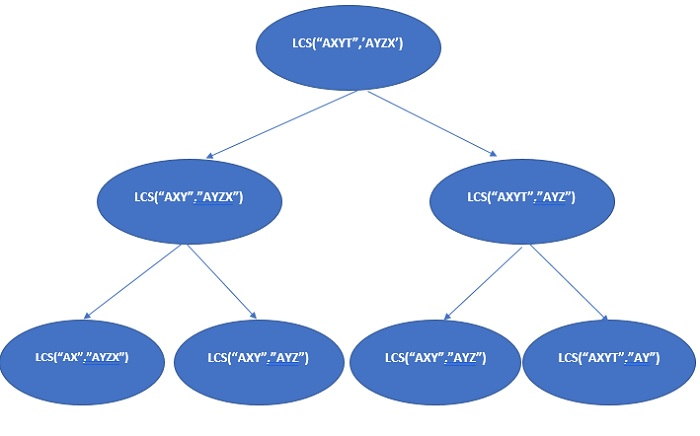
在上述的遞歸樹中，lcs("AXY", "AYZ") 解決了多次。

由於這個問題具有重疊子結構的特性，可以透過使用記憶化或表格化來避免對相同子問題的重複計算。

遞歸程式碼的記憶化方法實作如下。

範例

import java.io.*;
import java.lang.*;
class testClass {
   final static int maxSize = 1000;
   public static int arr[][] = new int[maxSize][maxSize];
   public static int calculatelcs(String str_1, String str_2, int m, int n) {
      if (m == 0 || n == 0)
         return 0;
      if (arr[m - 1][n - 1] != -1)
         return arr[m - 1][n - 1];
      if (str_1.charAt(m - 1) == str_2.charAt(n - 1)) {
         arr[m - 1][n - 1] = 1 + calculatelcs(str_1, str_2, m - 1, n - 1);
         return arr[m - 1][n - 1];
      }
      else {
         int a = calculatelcs(str_1, str_2, m, n - 1);
         int b = calculatelcs(str_1, str_2, m - 1, n);
         int max = (a > b) ? a : b;
         arr[m - 1][n - 1] = max;
         return arr[m - 1][n - 1];
      }
   }
   public static void main(String[] args) {
      for (int i = 0; i < 1000; i++) {
         for (int j = 0; j < 1000; j++) {
            arr[i][j] = -1;
         }
      }
      String str_1 = "AGGTAB";
      String str_2 = "GXTXAYB";
      System.out.println("Length of LCS is " + calculatelcs(str_1, str_2, str_1.length(),str_2.length()));
   }
}

輸出

如果我們執行上述程式碼，將會產生以下輸出

Length of LCS is 4

方法

觀察到在方法(calculatelcs)中有4個參數，其中有2個常數（不影響記憶化），還有2個非常數參數(m和n)，在每次遞歸呼叫方法時會改變其值。為了實現記憶化，我們引入一個二維數組來儲存計算過的lcs(m,n)的值，儲存在arr[m-1][n-1]中。當再次調用具有相同參數m和n的函數時，我們不再執行遞歸調用，而是直接返回arr[m-1][n-1]，因為先前計算的lcs(m, n)已經儲存在arr [m-1][n-1]中，因而減少了遞迴呼叫的次數。

三維記憶化

這是一種用於具有3個非常數參數的遞歸程式的記憶化方法。在這裡，我們以計算三個字串的LCS長度為例。

這裡的方法是產生給定字串的所有可能子序列（總共可能的子序列有3ⁿ個），並在其中匹配最長的公共子序列。

我們將引入一個三維表來儲存計算過的值。考慮到子序列。

• A1[1...i] i < N

• #A2[1...j] j < M

• A3[1...k] k < K

#如果我們找到一個公用字元(X[i]==Y[j ]==Z[k])，我們需要遞歸處理剩餘的字元。否則，我們將計算下列情況的最大值

• 保留X[i]遞歸處理其他字元

• 保留Y[j]遞歸處理其他字元

• 保留Z[k]遞歸處理其他字元

因此，如果我們將上述想法轉換為遞歸函數，則

f(N,M,K)={1 f(N-1,M-1,K-1)if (X[N]==Y[M]==Z[K]maximum(f (N-1,M,K),f(N,M-1,K),f(N,M,K-1))}

• f(N-1 ,M,K) = 保留X[i]遞歸處理其他字元

• f(N,M-1,K) = 保留Y[j]遞歸處理其他字元

• f(N,M,K-1) = 保留Z[k]遞歸處理其他字元

##範例

import java.io.IOException;
import java.io.InputStream;
import java.util.*;
class testClass {
   public static int[][][] arr = new int[100][100][100];
   static int calculatelcs(String str_1, String str_2, String str_3, int m, int n, int o) {
         for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= n; j++) {
               arr[i][j][0] = 0;
            }
         }
         for (int i = 0; i <= n; i++) {
            for (int j = 0; j <= o; j++) {
               arr[0][i][j] = 0;
            }
         }
         for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= o; j++) {
               arr[i][0][j] = 0;
            }
         }
         for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
               for (int k = 1; k <= o; k++) {
                  if (str_1.charAt(i - 1) == str_2.charAt(j-1) && str_2.charAt(j1) == str_3.charAt(k-1)) {
                     arr[i][j][k] = 1 + arr[i - 1][j - 1][k - 1];
                  }
                  else {
                     arr[i][j][k] = calculateMax(arr[i - 1][j][k], arr[i][j - 1][k], arr[i][j][k - 1]);
                  }
               }
            }
         }
         return arr[m][n][o];
   }
   static int calculateMax(int a, int b, int c) {
      if (a > b && a > c)
         return a;
         if (b > c)
         return b;
         return c;
   }
   public static void main(String[] args) {
      String str_1 = "clued";
      String str_2 = "clueless";
      String str_3 = "xcxclueing";
      int m = str_1.length();
      int n = str_2.length();
      int o = str_3.length();
      System.out.print("Length of LCS is " + calculatelcs(str_1, str_2, str_3, m, n, o));
   }
}

輸出

如果我們執行上述程式碼，將會產生以下輸出

Length of LCS is 4

以上是在Java中的記憶化（1D，2D和3D）動態規劃的詳細內容。更多資訊請關注PHP中文網其他相關文章！