美團面試：請手寫一個快排，被我懟了！

今天，這個主題是當時面試官叫我現場手寫快排，場景如下：

面試官：我們繼續來聊聊關於資料結構與演算法，你能寫一個快速排序？ （說話的同時，把我履歷反過來，遞給我一支筆，意思就是叫我在自己的履歷背後寫）

菜鳥我：什麼意思？這裡寫嗎？ （指著履歷）

面試官：嗯

菜鳥我：不會

面試官：好吧，今天面試就到這裡

菜鳥我：（心裡很火，勞資的簡歷，想在勞資簡歷上寫代碼？）沙雕

面試官：（回頭看了一眼，一臉懵逼）

想想自己還是太年輕了，換著是現在就不是這樣了。寫就寫嘛，反正不就是一張紙而已。

其實，快排說簡單嘛，估計很多人也手寫不出來，說難嗎也有很多人你能現場手寫幾種方式。

菜鳥我，當年還是能​​手寫一種，畢竟面試前我剛好刻意的準備過「默寫快排」。

下面，我們就來分析分析----快速排序。

背景

#來自百科全書：

快速排序由C. A. R. Hoare在1962年提出。它的基本想法是:透過一趟排序將要排序的資料分割成獨立的兩部分，其中一部分的所有資料都比另外一部分的所有資料都要小，然後再按此方法對這兩部分資料分別進行快速排序，整個排序過程可以[遞歸]進行，以此達到整個資料變成有序序列。

這概念理解起來 還是蠻費勁兒的。

可以這麼理解：

快速排序是冒泡排序的改良版，整個過程就在拆拆補補，東拆西補或西拆東補，一邊拆一邊補，直到所有元素達到有序狀態。

核心思想：

先從數列中取出一個數字作為基準數，然後進行大小分區；

分區過程，將比這個數大的數全放到它的右邊，小於或等於它的數全放到它的左邊；

再對左右區間重複第二步，直到各區間只有一個數，排序完成。

實作案例

#下面先透過圖文形式一步一步拆解。

拿[4,1,6,2,9,3]這個陣列舉例。

第一遍遍歷：

• First split [4,1,6,2,9,3] and select element 4 as the pivot point
• Check whether 1 < 4 (pivot point)
• Check if 6 < 4 (pivot point)
• Check if 2 < 4 (pivot point) Point)
• ##2 < 4 (pivot point) is true, exchange index 2 and stored index 6
• Check if 9 < 4 (pivot point)
##Check if 3 < 4 (pivot point)
• ##3 < 4 (axis center point) is true, exchange index 3 and storage index 6
• Exchange pivot point 4 and storage index 3
• At this time, the left side of pivot point 4 is less than 4, and the right side is greater than 4

The current array sequence is [3, 1, 2, 4, 9, 6].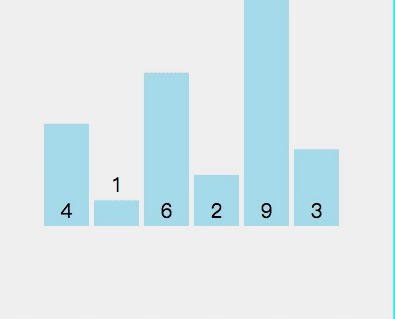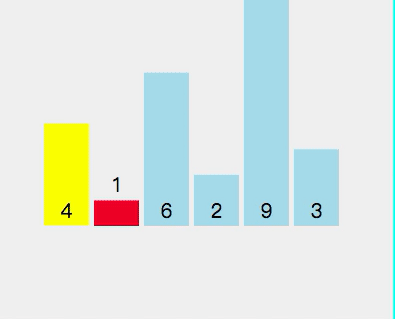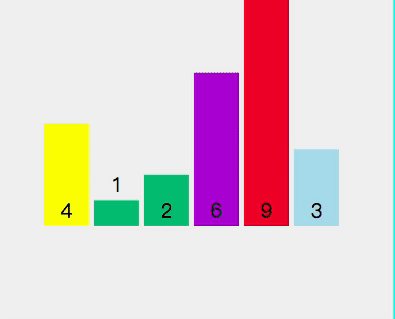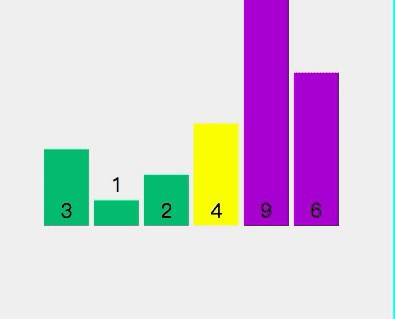

Next step:

Sort the left side first

• ##Select element 3 as the pivot point
• Check if 1 < 3 (pivot point)
• Check if 2 < 3 (pivot point)
• Exchange pivot point 3 and storage index value 2
• The pivot point is now at the sorted position
• Split [2,1] and select 2 as the pivot point
• Check whether 1 < 2 (pivot point)
• ## The traversal on the left is completed, and the pivot point 2 and the storage index 1 are exchanged.
• The same is true for the right... I will not describe them one by one to avoid visual fatigue. You can see the dynamic demonstration picture below.

2. The whole process of quick sorting

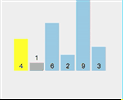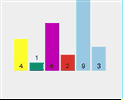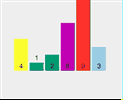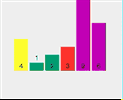
3. Code implementation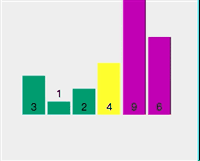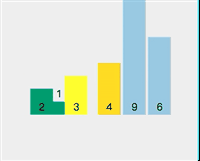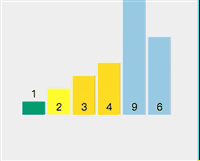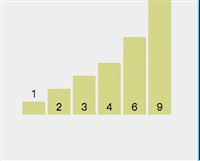

Below, we use Java language to implement the previous quick sort case:

import java.util.Arrays;

public class QuickSortDemo {
    //四个步骤：
    //1.比较startIndex和endIndex，更喜欢理解为校验
    //2.找出基准
    //3.左边部分排序
    //4.右边排序
    public static void quickSort(int[] arr, int startIndex, int endIndex) {
        if (startIndex < endIndex) {
            //找出基准
            int partition = partition(arr, startIndex, endIndex);
            //分成两边递归进行
            quickSort(arr, startIndex, partition - 1);
            quickSort(arr, partition + 1, endIndex);
        }
    }

    //找基准
    private static int partition(int[] arr, int startIndex, int endIndex) {
        int pivot = arr[startIndex];
        
        int left = startIndex;
        int right = endIndex;
        
        //等于就没有必要排序
        while (left != right) {
            
            while (left < right && arr[right] > pivot) {
                right--;
            }
          
            while (left < right && arr[left] <= pivot) {
                left++;
            }
            //找到left比基准大，right比基准小，进行交换
            if (left < right) {
                swap(arr, left, right);
            }
        }
        //第一轮完成，让left和right重合的位置和基准交换，返回基准的位置
        swap(arr, startIndex, left);
        return left;
    }

    //两数交换
    public static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

    public static void main(String[] args) {
        int[] a = {3, 1, 2, 4, 9, 6};
        quickSort(a, 0, a.length - 1);
        //输出结果
        System.out.println(Arrays.toString(a));
    }
}

Output result:

[1, 2, 3, 4, 6, 9]

Code implementation, it is recommended to combine it with the previous animation to make it easier to understand.

There are several ways to write quick sort. If you are interested, you can look it up yourself. You can also look at how quick sort is introduced in Wikipedia.

4. Complexity analysis

Time complexity:

Worst The situation is that the element taken each time is the smallest/largest in the array. This situation is actually bubble sorting (the order of one element is arranged every time)

The time complexity in this case is good Calculated, it is the time complexity of bubble sort: T[n] = n * (n-1) = n^2 n;

The best case is O(nlog2n), derivation The process is as follows:

(Time complexity formula of recursive algorithm: T[n] = aT[n/b] f(n) )

https://img2018.cnblogs.com/blog/1258817/201903/1258817-20190326191158640-601403776.png

So The average time complexity is O(nlog2n)

Space complexity:

The space used by quick sort is O(1), which is a constant level; and what really consumes space is the recursive call. Because some data must be maintained for each recursion:

The space complexity in the optimal case is: O(log2n); when the group is divided equally every time

The worst case space complexity is: O(n); it degenerates into bubble sorting

So the average space complexity is O(log2n)

5. Summary of quick sorting method

• The first element is taken as the pivot point by default (pivot point The confirmation distinguishes two algorithms: "quick sorting method" and "random sorting method"), and random sorting randomly rands an element as the pivot point;
• If the two are not consistent Neighbor element exchange can eliminate multiple reverse orders in one exchange and speed up the sorting process.

Postscript

Finally, do you think quick sort is useful at work? ? I have never used it after working for nearly ten years, but I know the idea of ​​​​quick queue. If I don’t prepare before the interview, I definitely won’t be able to write it anyway. What about you?

以上是美團面試：請手寫一個快排，被我懟了！的詳細內容。更多資訊請關注PHP中文網其他相關文章！