查詢從節點X開始,距離最多為D的子樹中的最小權重

在進行電腦程式設計時,有時需要求出源自特定節點的子樹的最小權重,條件是該子樹不能包含距離指定節點超過D個單位的節點。這個問題出現在各個領域和應用中,包括圖論、基於樹的演算法和網路最佳化。
子樹是較大樹結構的子集,指定的節點作為子樹的根節點。子樹包含根節點的所有後代及其連接邊。節點的權重是指分配給該節點的特定值,可以表示其重要性、重要性或其他相關指標。在這個問題中,目標是找到子樹中所有節點中的最小權重,同時將子樹限制在距離根節點最多D個單位的節點。
在下面的文章中,我們將深入研究從子樹中挖掘最小權重的複雜性,該子樹的邊界不超過來自節點 X 的 D 距離節點。
方法
方法1 - 深度優先搜尋(DFS),解決此問題的最常見和最直接的方法之一是使用子樹的深度優先搜尋(DFS) 遍歷.
方法2 − 解決這個問題的另一種方法是使用廣度優先搜尋(BFS)遍歷子樹。
文法
下面的語法宣告了一個名為findMinimumWeight的函數,它接受兩個參數。第一個參數Node* x是指向二元樹中一個節點的指針,第二個參數int d是表示距離的整數。該函數傳回一個整數minWeight。在給定的程式碼片段中沒有指定從節點x開始的子樹中找到最小權重的演算法的實作。
int findMinimumWeight(Node* x, int d) {
// Implementation of the algorithm
// ...
return minWeight;
}
哪裡 -
Node* x 表示指向樹的根節點的指標。
int d 表示子樹中節點與根節點之間的最大距離的限制。
演算法
電腦科學中一個複雜的挑戰是確定從給定節點X開始,跨越不超過D個節點的子樹的最小權重。有幾種演算法可以解決這個問題。在這裡,我們提供了一個高級概述的方法−
步驟 1 - 從節點 X 作為子樹的根開始。
步驟 2 - 以深度優先的方式遍歷子樹,仔細記錄每個節點與根節點的距離。
第 3 步 - 維護一個變數來追蹤迄今為止遇到的最小重量。
步驟4 - 在每個節點上,評估從根節點到該節點的距離是否在D限制範圍內。如果是,則使用目前節點的權重更新最小權重變數。
步驟 5 - 對子樹中的所有節點重複步驟 3 和 4。
第6步 - 最終,傳回從子樹獲得的最小權重。
方法 1
應對這項挑戰的最簡單且最普遍的解決方案之一是利用子樹的深度優先搜尋 (DFS) 探索。在這種方法中,我們以深度優先的方式遍歷給定節點的子樹,在進入下一個兄弟節點之前訪問每個節點及其後代。在每個節點,我們評估其與根節點的距離,如果它落在指定的限制內,我們將修改迄今為止發現的最小權重。此方法的運行時間複雜度為 O(n),其中 n 表示子樹中的節點數,因為每個節點僅被存取一次。
範例
所提供的程式碼構成了一個程序,旨在確定子樹中距離二元樹中的節點「X」至多「d」距離的節點的最小權重。二元樹由稱為「節點」的結構表示,該結構包含權重、對其左子節點的引用以及對其右子節點的引用。
主函數「findMinimumWeightDFS」以節點「x」和整數「d」作為輸入,並傳回距「x」最多「d」距離的節點的最小權重。該函數使用輔助函數“findMinimumWeightDFS”,該函數在二元樹上執行深度優先搜尋(DFS)並更新迄今為止發現的最小權重。
最小權重被初始化為一個較大的值,並在DFS探索過程中進行修改,如果當前節點距離根節點最多為'd'距離。函數在DFS探索後傳回找到的最終最小權重。
#include <iostream>
#include <climits>
using namespace std;
// Definition of Node structure
struct Node {
int weight;
Node* left;
Node* right;
Node(int w) : weight(w), left(nullptr), right(nullptr) {}
};
// Function to perform DFS traversal and find minimum weight
void findMinimumWeightDFS(Node* x, int d, int distance, int& minWeight) {
// Base case: if the current node is null or distance exceeds D, return
if (x == nullptr || distance > d) {
return;
}
// If the current node is at most D-distant from the root node, update minWeight
if (distance <= d) {
minWeight = min(minWeight, x->weight);
}
// Recursively perform DFS on the left and right children of the current node
findMinimumWeightDFS(x->left, d, distance + 1, minWeight);
findMinimumWeightDFS(x->right, d, distance + 1, minWeight);
}
// Function to find minimum weight from subtree of at most D-distant nodes from node X using DFS
int findMinimumWeightDFS(Node* x, int d) {
int minWeight = INT_MAX; // Initialize minWeight to a large value
findMinimumWeightDFS(x, d, 0, minWeight); // Perform DFS traversal
return minWeight; // Return the minimum weight obtained
}
// Driver code
int main() {
// Create a sample binary tree
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
root->right->left = new Node(6);
root->right->right = new Node(7);
// Test the findMinimumWeightDFS function
int d = 2;
int minWeight = findMinimumWeightDFS(root, d);
cout << "Minimum weight from subtree of at most " << d << "-distant nodes from node X: " << minWeight << endl;
return 0;
}
輸出
Minimum weight from subtree of at most 2-distant nodes from node X: 1
方法2
解決這個挑戰的另一個策略是採用廣度優先搜尋(BFS)對子樹進行探索。在這種方法中,我們以廣度優先的方式遍歷給定節點的子樹,在繼續到下一層之前訪問所有節點的子節點。在每個節點,我們評估它與根節點的距離,如果它在指定的限制範圍內,我們修改迄今為止發現的最小權重。此方法的時間複雜度為O(n),其中n表示子樹中的節點數,因為每個節點只造訪一次。然而,這種方法的空間複雜度比深度優先搜尋(DFS)方法更大,因為它需要一個佇列來追蹤要探索的節點。
示例
该代码构成了一个程序,旨在确定二叉树中节点的最小权重,给定距根节点的最大距离“d”。该策略涉及对二叉树进行广度优先搜索 (BFS) 探索,并将每个节点及其与根节点的距离存储在队列中。该函数以根节点及其距离为 0 启动,并将其添加到队列中。
然后,它迭代地从队列的前面检索节点,如果节点的距离至多为“d”,则更新最小权重。如果该节点拥有左或右后代,它会将孩子添加到具有更新距离的队列中。该函数将继续执行,直到队列为空。最后,函数返回BFS探索得到的最小权重。
#include <iostream>
#include <queue>
#include <climits>
using namespace std;
// Definition of Node structure
struct Node {
int weight;
Node* left;
Node* right;
Node(int w) : weight(w), left(nullptr), right(nullptr) {}
};
// Function to perform BFS traversal and find minimum weight
int findMinimumWeightBFS(Node* x, int d) {
queue<pair<Node*, int>>q; // Create a queue to store nodes and their distances
q.push({x, 0}); // Push the root node and its distance (0) to the queue
int minWeight = INT_MAX; // Initialize minWeight to a large value
while (!q.empty()) {
Node* curr = q.front().first; // Get the current node from the front of the queue
int distance = q.front().second; // Get the distance of the current node from the root
q.pop(); // Pop the current node from the queue
// If the current node is at most D-distant from the root node, update minWeight
if (distance <= d) {
minWeight = min(minWeight, curr->weight);
}
// If the current node has left child, push it to the queue with updated distance
if (curr->left) {
q.push({curr->left, distance + 1});
}
// If the current node has right child, push it to the queue with updated distance
if (curr->right) {
q.push({curr->right, distance + 1});
}
}
return minWeight; // Return the minimum weight obtained
}
// Driver code
int main() {
// Create a sample binary tree
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
root->right->left = new Node(6);
root->right->right = new Node(7);
// Test the findMinimumWeightBFS function
int d = 2;
int minWeight = findMinimumWeightBFS(root, d);
cout << "Minimum weight from subtree of at most " << d << "-distant nodes from node X: " << minWeight << endl;
return 0;
}
输出
Minimum weight from subtree of at most 2-distant nodes from node X: 1
结论
本文介绍了如何使用 C++ 从二叉树中与特定节点 X 相距最多 D 距离的节点子树中获取最小权重。我们研究了深度优先搜索 (DFS) 和广度优先搜索 (BFS) 方法,并提供了每种方法的实现代码和示例结果。
以上是查詢從節點X開始,距離最多為D的子樹中的最小權重的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

熱門話題
 12306怎麼查詢歷史購票紀錄 查看歷史購票紀錄的方法
Mar 28, 2024 pm 03:11 PM
12306怎麼查詢歷史購票紀錄 查看歷史購票紀錄的方法
Mar 28, 2024 pm 03:11 PM
12306訂票app下載最新版是一款大家非常滿意的出行購票軟體,想去哪裡就去那裡非常方便,軟體內提供的票源非常多,只需要通過實名認證就能在線購票,所有用戶的出行車票機票都可以輕鬆買到,享受不同的優惠折扣。還能提前開啟預約搶票,預約飯店、專車接送都是可以的,有了它想去哪裡就去那裡一鍵購票,出行更加簡單方便,讓大家的出行體驗更舒服,現在小編在線詳細為12306用戶帶來查看歷史購票記錄的方法。 1.打開鐵路12306,點擊右下角我的,點擊我的訂單 2.在訂單頁面點擊已支付。 3.在已支付頁
 學信網如何查詢自己的學歷
Mar 28, 2024 pm 04:31 PM
學信網如何查詢自己的學歷
Mar 28, 2024 pm 04:31 PM
學信網如何查詢自己的學歷?在學信網中是可以查詢到自己的學歷,很多用戶都不知道如何在學信網中查詢到自己的學歷,接下來就是小編為用戶帶來的學信網查詢自己學歷方法圖文教程,感興趣的用戶快來一起看看吧!學信網使用教程學信網如何查詢自己的學歷一、學信網入口:https://www.chsi.com.cn/二、網站查詢:第一步:點選上方學信網位址,進入首頁點選【學歷查詢】;第二步:在最新的網頁中點選如下圖箭頭所示的【查詢】;第三步:之後在新頁面點選【的登陸學信檔案】;第四步:在登陸頁面輸入資料點選【登陸】;
 MySQL與PL/SQL的異同比較
Mar 16, 2024 am 11:15 AM
MySQL與PL/SQL的異同比較
Mar 16, 2024 am 11:15 AM
MySQL與PL/SQL是兩種不同的資料庫管理系統,分別代表了關係型資料庫和過程化語言的特性。本文將比較MySQL和PL/SQL的異同點,並附帶具體的程式碼範例進行說明。 MySQL是一種流行的關聯式資料庫管理系統,採用結構化查詢語言(SQL)來管理和操作資料庫。而PL/SQL是Oracle資料庫特有的過程化語言,用於編寫預存程序、觸發器和函數等資料庫物件。相同
 蘋果手機怎麼查詢啟動日期
Mar 08, 2024 pm 04:07 PM
蘋果手機怎麼查詢啟動日期
Mar 08, 2024 pm 04:07 PM
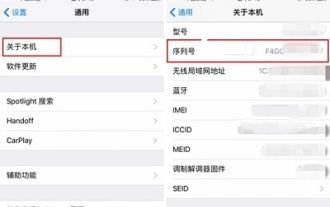
使用蘋果手機想要查詢啟動日期,最好的方法是透過手機中的序號來查詢,也可以透過存取蘋果的官網來進行查詢,透過連接電腦查詢,下載第三方軟體查詢。蘋果手機怎麼查詢啟動日期答:序號查詢,蘋果官網查詢,電腦查詢,第三方軟體查詢1、用戶最好的方式就是知道自己手機的序號,開啟設定通用關於本機就可以看到序號。 2.使用序號不僅可以知道自己手機的啟動日期,還可以查看手機版本,手機產地,手機出廠日期等。 3.用戶訪問蘋果的官網找到技術支持,找到頁面底部的服務和維修欄目,裡面查看iPhone的激活信息。 4.用戶
 如何使用Oracle 查詢表是否被鎖?
Mar 06, 2024 am 11:54 AM
如何使用Oracle 查詢表是否被鎖?
Mar 06, 2024 am 11:54 AM
標題:如何使用Oracle查詢表格是否被鎖定?在Oracle資料庫中,表鎖是指當一個事務正在對錶執行寫入操作時,其他事務想要對該表執行寫入操作或對表進行結構改變(如增加列、刪除行等)時會被阻塞。在實際開發過程中,我們經常需要查詢表格是否被鎖,以便更好地排除和處理相關問題。本文將介紹如何使用Oracle語句查詢表格是否被鎖,並給出具體的程式碼範例。要查詢表是否被鎖,我們
 Discuz資料庫位置查詢技巧分享
Mar 10, 2024 pm 01:36 PM
Discuz資料庫位置查詢技巧分享
Mar 10, 2024 pm 01:36 PM
論壇是網路上非常常見的網站形式之一,它為使用者提供了一個分享資訊、交流討論的平台。而Discuz是一款常用的論壇程序,相信很多站長都已經非常熟悉了。在進行Discuz論壇的開發和管理過程中,經常需要查詢資料庫中的資料來進行分析或處理。在這篇文章中,我們將分享一些查詢Discuz資料庫位置的技巧,並提供具體的程式碼範例。首先,我們需要了解Discuz的資料庫結構
 如何查詢BitTorrent幣最新價格?
Mar 06, 2024 pm 02:13 PM
如何查詢BitTorrent幣最新價格?
Mar 06, 2024 pm 02:13 PM
查詢BitTorrent幣(BTT)最新價格BTT是TRON區塊鏈上的加密貨幣,用於獎勵BitTorrent網路用戶分享和下載檔案。尋找BTT最新價格的方法如下:選擇一個可靠的價格查詢網站或應用程式。一些常用的價格查詢網站包括:CoinMarketCap:https://coinmarketcap.com/Coindesk:https://www.coindesk.com/幣安:https://www.binance.com/在網站或應用程式中搜尋BTT。查看BTT的最新價格。注意:加密貨幣價格
 如何查詢通神幣最新價格?
Mar 21, 2024 pm 02:46 PM
如何查詢通神幣最新價格?
Mar 21, 2024 pm 02:46 PM
如何查詢通神幣最新價格?通神幣是一種數位貨幣,可用於購買遊戲內物品、服務和資產。它是去中心化的,意味著它不受政府或金融機構的控制。通神幣的交易在區塊鏈上進行,這是一個分散式帳本,記錄了所有通神幣交易的資訊。要查詢通神幣的最新價格,您可以使用以下步驟:選擇一個可靠的價格來查詢網站或應用程式。一些常用的價格查詢網站包括:CoinMarketCap:https://coinmarketcap.com/Coindesk:https://www.coindesk.com/幣安:https://www.bin






