具有最多M個連續節點且值為K的從根到葉子的路徑數量
簡介
二元樹是一種令人著迷的資料結構,在電腦科學和程式設計中有著廣泛的應用。一個有趣的問題是從給定的由父節點及其子節點組成的樹中尋找計數。二元樹由節點組成,根節點決定,根節點可以根據使用者需求給出子節點。 K值決定,移動方式由M值選擇。
根到葉路徑的計數
該圖是使用各種節點創建的,這些節點保存整數形式的值。本文主要關注從起始節點或根節點到葉節點或子節點的計數。
範例
該圖是從具有各種節點的二元樹創建的。
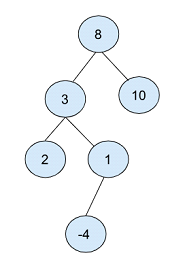
#在上面的二元樹中,根節點選擇為「8」。
接著建立兩個節點,一個值為 3,另一個值為 10,佔據根節點的左右位置。
以值為 2 的節點為根,建立另一個子節點,其值分別為 2 和 1 作為左節點和右節點。
最後,值為 1 的子節點建立值為 -4 的子節點。
方法 1:使用遞迴函數計算由最多 M 個具有 K 值的連續節點組成的根到葉路徑的 C 程式碼
為了有效地解決這個問題,我們將利用樹遍歷演算法和遞歸等基本概念。
演算法
第 1 步:建立一個用於表示樹節點的結構,其中包括兩個指標(左子節點和右子節點)以及用於儲存節點值的整數欄位。
第2 步:設計一個遞歸函數,從根開始遍歷二元樹,同時追蹤當前路徑長度(初始化為0)、連續出現次數(初始設定為0)、目標值K,允許的最大連續出現次數M。
第 3 步:在每個左子樹和右子樹上遞歸呼叫函數,並傳遞更新的參數,例如遞增的路徑長度和連續出現次數(如果適用)。
第4步:對於遍歷過程中每個訪問過的非空節點:
a) 如果其值等於 K,則將兩個變數都加一。
b) 如果其值與 K 不符或超過迄今為止在路徑中已遇到的 M 連續出現次數,則將變數重設為零。
第5步:在遍歷樹時,如果子節點在左和右兩種情況下的值都為零 - 我們可以用兩種方式處理,即
a) 檢查變數是否不超過M。
b) 如果是,則將滿足條件的路徑總數增加 1。
範例
//including the all in one header
#include<bits/stdc++.h>
using namespace std;
//creating structure with two pointers as up and down
struct Vertex {
int data;
struct Vertex* up;
struct Vertex* down;
};
//countPaths function declared with five arguments ; with root = end; Node= vertex; left = up; right = down
int countPaths(Vertex* end, int K, int M, int currCount, int
consCount) {
//To check the condition when the root is equal to 1 and greater than the maximum value, the values is incremented
if (end == NULL || consCount > M) {
return 0;
}
//To check when the root is equal to the K value, increment by 1
if (end->data == K) {
currCount++;
consCount++;
} else {
//If it is not equal, it will return 0
currCount = 0;
}
if (end->up == NULL && end->down == NULL) {
if (currCount <= M) {
return 1;
} else {
return 0;
}
}
return countPaths(end->up, K, M, currCount, consCount) + countPaths(end->down, K, M, currCount, consCount);
}
//Main function to test the implementation
int main() {
Vertex* end = new Vertex();
end->data = 8;
end->up = new Vertex();
end->up->data = 3;
end->down = new Vertex();
end->down->data = 10;
end->up->up = new Vertex();
end->up->up->data = 2;
end->up->down = new Vertex();
end->up->down->data = 1;
end->up->down->up = new Vertex();
end->up->down->up->data = -4;
int K = 1; // Value of node
int M = 2; // Maximum consecutive nodes
int currCount = -1; // Current count
int consCount = -1; // Consecutive count
cout << "The number of paths obtained from the given graph of" << M << "nodes with a value of " << K << " is " << countPaths(end, K, M, currCount, consCount) << endl;
return 0;
}
輸出
The number of paths obtained from the given graph of 2 nodes with a value of 1 is 3
結論
在本文中,我們探討了計算從頂部(即葉)到末端或根的路徑數的問題。透過使用 C 中的樹遍歷演算法和遞歸技術,可以有效地解決此類問題。遍歷二元樹的過程看起來很困難,但透過範例就變得簡單了。
以上是具有最多M個連續節點且值為K的從根到葉子的路徑數量的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

熱門話題
 什麼是MD5哈希值?
Feb 18, 2024 pm 08:50 PM
什麼是MD5哈希值?
Feb 18, 2024 pm 08:50 PM
MD5值是什麼?在電腦科學中,MD5(MessageDigestAlgorithm5)是一種常用的雜湊函數,用於對訊息進行摘要或加密。它產生一個固定長度的128位二進位數字,通常以32位的十六進位表示。 MD5演算法由RonaldRivest於1991年設計。儘管在密碼學領域中,MD5演算法被認為不再安全,但它仍廣泛應用於資料完整性驗證和檔案校驗等方
 PHP值解析:詳解PHP中位數的概念及應用
Mar 21, 2024 pm 09:06 PM
PHP值解析:詳解PHP中位數的概念及應用
Mar 21, 2024 pm 09:06 PM
PHP值解析:詳解PHP中值的概念及應用在PHP程式中,值是一個非常基礎且重要的概念。在本文中,我們將深入探討PHP中位數的概念及其在實際編程中的應用。我們將從基本值類型,變量,數組,物件和常數等方面進行詳細解析,並提供具體的程式碼範例,幫助讀者更好地理解和運用PHP中的值。基本值型別在PHP中,最常見的基本值型別包括整數型,浮點型,字串,布林型和空值。這些基本
 探討Go語言中不可尋址的值
Mar 25, 2024 am 09:33 AM
探討Go語言中不可尋址的值
Mar 25, 2024 am 09:33 AM
在Go語言中,有一些值是不可尋址的,即無法取得它們的記憶體位址。這些值包括常數、字面量和不能被取位址的表達式。在本文中,我們將探討這些不可尋址的值,並透過具體的程式碼範例來理解它們的特性。首先,我們來看一些常數的例子。在Go語言中,常數是不可尋址的,因為常數是在編譯時就確定其值的,不存在運行時的記憶體位址可供存取。下面是一個範例程式碼:packagemaini
 使用C++編程,找到在網格中從一個點到另一個點的路徑數
Aug 29, 2023 pm 10:25 PM
使用C++編程,找到在網格中從一個點到另一個點的路徑數
Aug 29, 2023 pm 10:25 PM
在本文中,我們給了一個問題,我們需要找到從點A到點B的總路徑數,其中A和B是固定點,即A是網格中的左上角點,B是網格中的右下角點,例如−Input:N=5Output:252Input:N=4Output:70Input:N=3Output:20在給定的問題中,我們可以透過簡單的觀察來形式化答案並得出結果。尋找解決方案的方法在這種方法中,我們透過觀察得出一個公式,即從A到B穿過網格時,我們需要向右行進n次,向下行進n次,這意味著我們需要找到所有可能的路徑組合,因此我們得到了
 Java 8中的Optional類別:如何使用filter()方法過濾可能為空的值
Aug 01, 2023 pm 05:27 PM
Java 8中的Optional類別:如何使用filter()方法過濾可能為空的值
Aug 01, 2023 pm 05:27 PM
Java8中的Optional類別:如何使用filter()方法過濾可能為空的值在Java8中,Optional類別是一個非常有用的工具,它允許我們更好地處理可能為空的值,避免了NullPointerException的發生。 Optional類別提供了許多方法來操作潛在的空值,其中一個重要的方法是filter()。 filter()方法的作用是,如果Option
 使用C++找到K叉樹中權重為W的路徑數
Sep 16, 2023 pm 06:09 PM
使用C++找到K叉樹中權重為W的路徑數
Sep 16, 2023 pm 06:09 PM
在本文中,我們將使用C++來計算K叉樹中權重為W的路徑數。我們已經給了一個K叉樹,它是一棵每個節點有K個子節點且每條邊都有一個權重的樹,權重從1到K遞減從一個節點到其所有子節點。我們需要計算從根節點開始的累積路徑數,這些路徑具有權重為W且至少有一條邊的權重為M。所以,這是一個例子:Input:W=4,K=3,M=2Output:6在給定的問題中,我們將使用dp來減少時間和空間複雜度。透過使用記憶化,我們可以使我們的程序更快,並使其適用於更大的約束。方法在這個方法中,我們將遍歷樹,並追蹤使用
 探索Java Map的魅力,破解資料處理的難題
Feb 19, 2024 pm 07:03 PM
探索Java Map的魅力,破解資料處理的難題
Feb 19, 2024 pm 07:03 PM
Map的講解Map是一種資料結構,允許你儲存鍵值對,鍵是唯一的,值可以是任何類型的物件。 Map介面提供了儲存和檢索鍵值對的方法,以及允許你遍歷Map中的鍵值對。 Map的類型Java中Map有幾種不同的實現,最常見的是HashMap、TreeMap和LinkedHashMap。 HashMap:一個基於散列表的Map實現,具有快速查找、插入和刪除的特點,但它不是有序的,這意味著鍵值對的順序在Map中是任意決定的。 TreeMap:一個基於紅黑樹的Map實現,具有快速查找、插入和刪除的特點,並且它是帶有
 當在JavaScript中將某個值轉換為布林值時會發生什麼?
Sep 02, 2023 am 09:21 AM
當在JavaScript中將某個值轉換為布林值時會發生什麼?
Sep 02, 2023 am 09:21 AM
使用JavaScript中的Boolean()方法轉換為布林值。您可以嘗試執行以下程式碼來了解如何在JavaScript中將[50,100]轉換為布林值。範例即時示範<!DOCTYPEhtml><html> <body> <p>Convert[50,100]toBoolean</p> &






