在C編程中,將序列2、6、12、20、30的前N項求和

要求這個級數的總和,我們先分析這個級數。
此級數是:2,6,12,20,30…
範例
For n = 6 Sum = 112 On analysis, (1+1),(2+4),(3+9),(4+16)... (1+1<sup>2</sup>), (2+2<sup>2</sup>), (3+3<sup>2</sup>), (4+4<sup>2</sup>), can be divided into two series i.e. s1:1,2,3,4,5… andS2: 1<sup>2</sup>,<sup>2</sup>,3<sup>2</sup>,....
使用數學公式求出第一個和第二個總和
Sum1 = 1+2+3+4… , sum1 = n*(n+1)/2 Sum2 = 12+2<sup>2</sup>+3<sup>2</sup>+4<sup>2</sup>… , sum1 = n*(n+1)*(2*n +1)/6
範例
#include <stdio.h>
int main() {
int n = 3;
int sum = ((n*(n+1))/2)+((n*(n+1)*(2*n+1))/6);
printf("the sum series till %d is %d", n,sum);
return 0;
}輸出
The sum of series till 3 is 20
以上是在C編程中,將序列2、6、12、20、30的前N項求和的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

熱門話題
 使用C++編寫程式碼,找到第N個非平方數
Aug 30, 2023 pm 10:41 PM
使用C++編寫程式碼,找到第N個非平方數
Aug 30, 2023 pm 10:41 PM
我們都知道不是任何數字的平方的數字,如2、3、5、7、8等。非平方數有N個,不可能知道每個數字。因此,在本文中,我們將解釋有關無平方數或非平方數的所有內容,以及在C++中尋找第N個非平方數的方法。第N個非平方數如果一個數是整數的平方,則該數稱為完全平方數。完全平方數的一些例子是-1issquareof14issquareof29issquareof316issquareof425issquareof5如果一個數不是任何整數的平方,則該數稱為非平方數。例如,前15個非平方數是-2,3,5,6,
 使用C++編寫的陣列右旋轉的反轉演算法
Sep 08, 2023 pm 08:17 PM
使用C++編寫的陣列右旋轉的反轉演算法
Sep 08, 2023 pm 08:17 PM
在本文中,我們將了解逆轉演算法,將給定的陣列向右旋轉k個元素,例如−Input:arr[]={4,6,2,6,43,7,3,7},k= 4Output:{43,7,3,7,4,6,2,6}Explanation:Rotatingeachelementofarrayby4-elementtotherightgives{43,7,3,7,4,6,2,6}.Input:arr[]={8 ,5,8,2,1,4,9,3},k=3Output:{4,9,3,8,5,8,2,1}尋找解的方
 在C編程中,求圓的面積
Aug 25, 2023 pm 10:57 PM
在C編程中,求圓的面積
Aug 25, 2023 pm 10:57 PM
圓是封閉圖形。圓上的所有點到圓內一點的距離都相等。中心點稱為圓心。點到圓心的距離稱為半徑。面積是封閉圖形尺寸跨距的定量表示。圓的面積是圓的尺寸內所包圍的面積。計算圓面積的公式,Area=π*r*r為了計算面積,我們給出了圓的半徑作為輸入,我們將使用公式來計算面積,算法STEP1:Takeradiusasinputfromtheuserusingstdinput.STEP2:Calculatetheareaofcircleusing, area=(
 使用C++找到數組中唯一配對的數量
Sep 07, 2023 am 11:53 AM
使用C++找到數組中唯一配對的數量
Sep 07, 2023 am 11:53 AM
我們需要適當的知識才能在C++的數組語法中創建幾個唯一的對。在尋找唯一對的數量時,我們計算給定數組中的所有唯一對,即可以形成所有可能的對,其中每個對應該是唯一的。例如-Input:array[]={5,5,9}Output:4Explanation:Thenumberofalluniquepairsare(5,5),(5,9),(9,5)and(9,9).Input:array[]= {5,4,3,2,2}Output:16尋找解法的方法有兩種方法可以解決這個問題,它們是−
 使用C++編寫程式碼,找到具有相同最小值和最大值的子數組的數量
Aug 25, 2023 pm 11:33 PM
使用C++編寫程式碼,找到具有相同最小值和最大值的子數組的數量
Aug 25, 2023 pm 11:33 PM
在本文中,我們將使用C++解決尋找最大值和最小值相同的子數組數量的問題。以下是該問題的範例−Input:array={2,3,6,6,2,4,4,4}Output:12Explanation:{2},{3},{6},{6},{2 },{4},{4},{4},{6,6},{4,4},{4,4}and{4,4,4}arethesubarrayswhichcanbeformedwithmaximumandminimumelementsame.Input:array={3,3, 1,5,
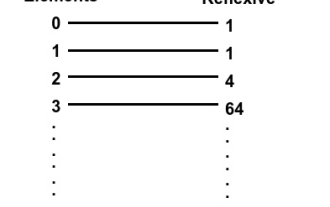 使用C++編寫,找出一個集合上的自反關係的數量
Aug 26, 2023 pm 08:17 PM
使用C++編寫,找出一個集合上的自反關係的數量
Aug 26, 2023 pm 08:17 PM
在本文中,我們將解釋在一個集合上找到反身關係的方法。在這個問題中,我們給出一個數字n,以及一個由n個自然數組成的集合,我們必須確定反身關係的數量。反身關係-如果對集合A中的每個'a',(a,a)屬於關係R,則稱關係R是集合A上的反身關係。例如-Input:x=1Output:1Explanation:set={1},reflexiverelationsonA*A:{{1}}Input:x=2Output:4Explanation:set={1,2},reflexiverelationsonA*
 使用C++按給定大小將雙向鍊錶分組反轉
Sep 04, 2023 am 09:49 AM
使用C++按給定大小將雙向鍊錶分組反轉
Sep 04, 2023 am 09:49 AM
在這個問題中,我們得到一個指向鍊錶頭部的指標和一個整數k。在大小為k的群組中,我們需要反轉鍊錶。例如-Input:1<->2<->3<->4<->5(doublylinkedlist),k=3Output:3<->2<->1<->5<->4尋找解決方案的方法在這個問題中,我們將制定一個遞歸演算法來解決這個問題。在這種方法中,我們將使用遞歸並使用遞歸來解決問題。範例#include<iostream&
 使用C++編寫,找出前三個項為等差數列,後三個項為等比數列的四元組數量
Aug 30, 2023 pm 02:09 PM
使用C++編寫,找出前三個項為等差數列,後三個項為等比數列的四元組數量
Aug 30, 2023 pm 02:09 PM
在本文中,我們將描述找出四元數的所有可能方法,其中前3項採用A.P.,後3項採用G.P.。首先,我們將解釋算術級數(A.P.)和幾何級數(G.P.)的基本定義。算術級數(A.P.)-它是一個數字序列,其中公差(d)相同或恆定,表示兩個連續數字的差是恆定的。例如:1,3,5,7,9|d=2幾何級數(G.P.)-這是一個數字序列,其中公共比率(r)相同,這意味著我們可以透過乘以前一個號碼與固定號碼。例如:3、6、12、24、....|r=2在這個問題中,我們需要確定N個整數的陣列arr[]中有多少個






