使用C++找出在第L個與第R個索引之間只有設定位的數字

在給定的問題中,我們需要找到一個數字的值,該數字在給定的範圍L、R之間具有所有的設定位。例如 −
Input: L = 1, R = 5 Output: 62 Explanation: representation of given L and R in binary form is 0..0111110 Input: L = 1, R = 4 Output: 30 Explanation: representation of given L and R in binary form is 0..11110
找到解決方案的方法
在給定的問題中,我們將討論兩種方法,暴力法和高效方法。
暴力法
在這種方法中,我們只需遍歷給定的範圍,並將給定範圍內的所有2的冪相加,這將是我們的答案。
範例
#include<bits/stdc++.h>
using namespace std;
int main() {
int L = 1, R = 3; // the given range
int ans = 0; // our answer
for(int i = L; i <= R; i++) // traversing through the whole range
ans += pow(2, i); // adding values to the answer.
cout << ans << "\n";
}輸出
14
在這個方法中,我們只是遍歷範圍並簡單地將範圍內的數字的2的冪相加。這個程式的時間複雜度為O(N),其中N是我們範圍的大小。但是我們可以透過應用給定問題中的位知識來進一步改進時間複雜度。
高效的方法
在這個方法中,我們將簡單地建構一個公式來計算我們的答案。
範例
#include<bits/stdc++.h>
using namespace std;
int main() {
int L = 1, R = 3; // the given range
int ans = 0; // our answer
for(int i = L; i <= R; i++) // traversing through the whole range
ans += pow(2, i); // adding values to the answer.
cout << ans << "\n";
}輸出
14
在這個方法中,我們制定了一個計算答案的公式。
上述程式碼的解釋
如您所知,我們需要計算給定範圍內具有設定位的數字,因此在這種方法中,我們找到一個從0到R的所有位都設定的數字。然後我們需要從1到(L-1)中減去一個所有位元都設定的數字,因此我們制定了這個觀察結果。給定程式碼的總體時間複雜度為O(1),即常數時間複雜度,這意味著我們可以在常數時間內計算任何答案。
結論
本文將為「僅在L-th和R-th索引之間具有設定位的數字」編寫一個程式。我們也學習了解決此問題的C 程序和完整的方法(普通和高效)。我們可以使用其他語言(如C、Java、Python和其他語言)編寫相同的程式。希望您會發現本文有幫助。
以上是使用C++找出在第L個與第R個索引之間只有設定位的數字的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

熱門話題
 淺析Golang中的的位元操作(位元運算子)
Feb 24, 2023 pm 07:42 PM
淺析Golang中的的位元操作(位元運算子)
Feb 24, 2023 pm 07:42 PM
在電腦記憶體昂貴,處理能力有限的美好舊時光裡,用比較黑客範的位元運算方式去處理資訊是首選方式(某些情況下只能如此)。時至今日,直接使用位元運算仍然是許多計算領域中不可或缺的部分,例如底層系統編程,圖形處理,密碼學等。
 使用C++編寫程式碼,找到第N個非平方數
Aug 30, 2023 pm 10:41 PM
使用C++編寫程式碼,找到第N個非平方數
Aug 30, 2023 pm 10:41 PM
我們都知道不是任何數字的平方的數字,如2、3、5、7、8等。非平方數有N個,不可能知道每個數字。因此,在本文中,我們將解釋有關無平方數或非平方數的所有內容,以及在C++中尋找第N個非平方數的方法。第N個非平方數如果一個數是整數的平方,則該數稱為完全平方數。完全平方數的一些例子是-1issquareof14issquareof29issquareof316issquareof425issquareof5如果一個數不是任何整數的平方,則該數稱為非平方數。例如,前15個非平方數是-2,3,5,6,
 在C編程中,求圓的面積
Aug 25, 2023 pm 10:57 PM
在C編程中,求圓的面積
Aug 25, 2023 pm 10:57 PM
圓是封閉圖形。圓上的所有點到圓內一點的距離都相等。中心點稱為圓心。點到圓心的距離稱為半徑。面積是封閉圖形尺寸跨距的定量表示。圓的面積是圓的尺寸內所包圍的面積。計算圓面積的公式,Area=π*r*r為了計算面積,我們給出了圓的半徑作為輸入,我們將使用公式來計算面積,算法STEP1:Takeradiusasinputfromtheuserusingstdinput.STEP2:Calculatetheareaofcircleusing, area=(
 使用C++編寫的陣列右旋轉的反轉演算法
Sep 08, 2023 pm 08:17 PM
使用C++編寫的陣列右旋轉的反轉演算法
Sep 08, 2023 pm 08:17 PM
在本文中,我們將了解逆轉演算法,將給定的陣列向右旋轉k個元素,例如−Input:arr[]={4,6,2,6,43,7,3,7},k= 4Output:{43,7,3,7,4,6,2,6}Explanation:Rotatingeachelementofarrayby4-elementtotherightgives{43,7,3,7,4,6,2,6}.Input:arr[]={8 ,5,8,2,1,4,9,3},k=3Output:{4,9,3,8,5,8,2,1}尋找解的方
 使用C++找到數組中唯一配對的數量
Sep 07, 2023 am 11:53 AM
使用C++找到數組中唯一配對的數量
Sep 07, 2023 am 11:53 AM
我們需要適當的知識才能在C++的數組語法中創建幾個唯一的對。在尋找唯一對的數量時,我們計算給定數組中的所有唯一對,即可以形成所有可能的對,其中每個對應該是唯一的。例如-Input:array[]={5,5,9}Output:4Explanation:Thenumberofalluniquepairsare(5,5),(5,9),(9,5)and(9,9).Input:array[]= {5,4,3,2,2}Output:16尋找解法的方法有兩種方法可以解決這個問題,它們是−
 如何使用Java中的BitSet函數進行位元操作
Jun 26, 2023 pm 06:11 PM
如何使用Java中的BitSet函數進行位元操作
Jun 26, 2023 pm 06:11 PM
BitSet是Java的一個類,用於進行位元操作。可以將BitSet看作一個由二進位位元構成的數組,每一個二進位位元只能是0或1。 BitSet提供了一系列方法來進行位元操作,包括設定、清除、翻轉、取得等等。在Java中使用BitSet進行位元操作很簡單,以下我們來介紹一下具體操作步驟。一、建立一個BitSet物件BitSet物件可以透過兩種方式來建立:1.使用預設值創
 使用C++編寫程式碼,找到具有相同最小值和最大值的子數組的數量
Aug 25, 2023 pm 11:33 PM
使用C++編寫程式碼,找到具有相同最小值和最大值的子數組的數量
Aug 25, 2023 pm 11:33 PM
在本文中,我們將使用C++解決尋找最大值和最小值相同的子數組數量的問題。以下是該問題的範例−Input:array={2,3,6,6,2,4,4,4}Output:12Explanation:{2},{3},{6},{6},{2 },{4},{4},{4},{6,6},{4,4},{4,4}and{4,4,4}arethesubarrayswhichcanbeformedwithmaximumandminimumelementsame.Input:array={3,3, 1,5,
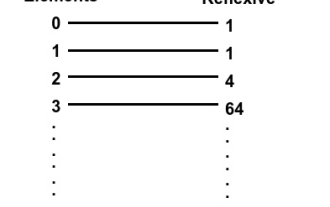 使用C++編寫,找出一個集合上的自反關係的數量
Aug 26, 2023 pm 08:17 PM
使用C++編寫,找出一個集合上的自反關係的數量
Aug 26, 2023 pm 08:17 PM
在本文中,我們將解釋在一個集合上找到反身關係的方法。在這個問題中,我們給出一個數字n,以及一個由n個自然數組成的集合,我們必須確定反身關係的數量。反身關係-如果對集合A中的每個'a',(a,a)屬於關係R,則稱關係R是集合A上的反身關係。例如-Input:x=1Output:1Explanation:set={1},reflexiverelationsonA*A:{{1}}Input:x=2Output:4Explanation:set={1,2},reflexiverelationsonA*






