樹中所有對最短路徑總和

在樹中,「所有節點對最短路徑總和」的術語指的是計算所有節點對的個別最短路徑的總和。一個有效的方法是使用雙重DFS(深度優先搜尋)演算法。在第一次DFS遍歷期間確定所選節點與每個其他節點之間的距離。在第二次DFS遍歷期間再次遍歷樹,將每個節點視為潛在的LCA(最低公共祖先),併計算所選LCA的後代節點對之間的距離總和。使用此方法可以計算出樹中所有節點對最短路徑總和,並確保得到理想的解決方案
使用的方法
雙重 DFS(深度優先搜尋)方法
動態規劃方法
雙重 DFS(深度優先搜尋)方法
對於樹中所有對最短路徑的總和,我們使用雙重 DFS(深度優先搜尋)方法,該方法涉及兩次 DFS 遍歷。首先,我們計算從任何節點開始到所有其他節點的距離。然後,在第二次 DFS 遍歷期間,我們導航樹,同時將每個節點視為潛在的 LCA。我們在遍歷時計算並求和作為所選 LCA 後代的節點對之間的距離。透過對所有節點重複此過程,我們獲得所有對最短路徑的總和。這個策略對於這個問題非常引人注目,因為它有效地計算了樹中所有節點集之間的距離總和。
演算法
樹中的任何節點都可以作為起始節點
為了確定從所選的起始節點到所有其他節點的距離,從該節點開始執行深度優先搜尋(DFS)。這些距離應該保存在一個陣列或資料結構中。
接下來,在樹上執行第二次深度優先搜尋(DFS),將每個節點視為可能的最近公共祖先(LCA)
在第二次 DFS 期間遍歷樹時,計算作為所選 LCA 後代的節點對之間的距離。對於每個 LCA,將這些距離加在一起。
對樹中的每個節點重複此過程
樹中最有限方式的所有符合的總和由步驟 4 中所有計算距離的總和表示。
Example
的中文翻譯為:範例
#include <iostream>
#include <vector>
using namespace std;
const int MAXN = 10005;
vector<int> graph[MAXN];
int ancestor[MAXN];
int dfs(int node, int lca, int distance) {
int sum = 0;
for (int neighbor : graph[node]) {
if (neighbor != lca) {
sum += dfs(neighbor, lca, distance + 1);
}
}
return sum + distance;
}
int main() {
int lca_node = 0;
int total_sum = 0;
for (int node = 0; node < MAXN; ++node) {
if (node != lca_node) {
total_sum += dfs(node, lca_node, 0);
}
}
cout << "Total sum of distances between descendants of the LCA: " << total_sum << endl;
return 0;
}
輸出
Total sum of distances between descendants of the LCA: 0
動態規劃方法:
我們首先選擇任一個節點作為根節點,並在動態規劃方法中將樹轉換為有根樹,用於計算樹中所有節點間最短路徑總和。我們利用動態規劃計算每個節點與根節點之間的分割,並將結果儲存在一個陣列中。然後,對於每個節點,我們將其子節點與根節點的分離(已計算)相加,以確定所有其他節點的整體分離。透過這種方式,我們能夠快速計算出所有節點間最短路徑的總數。作為解決此問題的有效方法,此演算法的時間複雜度為O(N),其中N是樹中節點的數量。
演算法
將樹中的任何節點作為根並以樹為根(例如,使用根節點的深度搜尋)以建立有根樹。
動態規劃可用來決定每個節點與根的距離。這些距離應該儲存在數組或資料結構中。
計算樹中每個節點到所有其他節點的距離的總和:
樹中所有對最短路徑的總和就是最終結果。
a.遍歷目前節點的子節點。
b.要考慮通過目前節點的路徑,請將每個子樹的子樹中的節點數以及先前為每個子樹計算的到根的距離相加。
c. 對於活動節點的每個子節點,將這些金額加總
d.將目前節點的總和加入最終結果。
#include <iostream>
#include <vector>
using namespace std;
struct TreeNode {
int val;
vector<TreeNode*> children;
};
int dfs(TreeNode* node, vector<int>& distances) {
int subtree_size = 1;
for (TreeNode* child : node->children) {
subtree_size += dfs(child, distances);
distances[node->val] += distances[child->val] + subtree_size;
}
return subtree_size;
}
int sumOfAllPairShortestPaths(TreeNode* root) {
vector<int> distances(root->val + 1, 0);
dfs(root, distances);
int total_sum = 0;
for (int distance : distances) {
total_sum += distance;
}
return total_sum;
}
int main() {
TreeNode* root = new TreeNode{0};
int result = sumOfAllPairShortestPaths(root);
cout << "Sum of all pair shortest paths in the tree: " << result << endl;
return 0;
}
輸出
Sum of all pair shortest paths in the tree: 0
結論
樹中所有對最短路徑的總和可以使用 Double DFS(深度優先搜尋)方法或動態規劃來計算。 Double DFS 方法由兩遍組成,首先計算從選定節點到所有其他節點的距離,然後再次遍歷樹,同時將每個節點視為潛在的最低公共祖先(LCA),以將之間的距離相加後代節點對。動態規劃方法需要遞歸地使用 DFS 來建立樹的根併計算從根到每個其他節點的距離。兩種方法的結果是相同的,並且由樹中所有成對最短路徑的總和組成。兩種演算法之間的決策可能基於特定的實現偏好或樹狀結構,但兩種演算法都提供了有效的解決方案。
以上是樹中所有對最短路徑總和的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 樹中所有對最短路徑總和
Aug 28, 2023 pm 03:17 PM
樹中所有對最短路徑總和
Aug 28, 2023 pm 03:17 PM
在樹中,「所有節點對最短路徑總和」的術語指的是計算所有節點對的個別最短路徑的總和。一個有效的方法是使用雙重DFS(深度優先搜尋)演算法。在第一次DFS遍歷期間確定所選節點與每個其他節點之間的距離。在第二次DFS遍歷期間再次遍歷樹,將每個節點視為潛在的LCA(最低公共祖先),併計算所選LCA的後代節點對之間的距離總和。使用這種方法可以計算出樹中所有節點對最短路徑總和,並確保得到一個理想的解決方案使用的方法雙重DFS(深度優先搜尋)方法動態規劃方法雙重DFS(深度優先搜尋)方法對於樹中所有對最短路徑的
 如何使用java實作最短路徑演算法
Sep 19, 2023 am 08:18 AM
如何使用java實作最短路徑演算法
Sep 19, 2023 am 08:18 AM
如何使用Java實現最短路徑演算法概述:最短路徑演算法是圖論中一個重要的應用,在網路路由、地圖導航等領域都有廣泛的應用。在這篇文章中,我們將學習如何使用Java實作最短路徑演算法,並提供具體的程式碼範例。演算法思維:最短路徑演算法有多種實作方式,其中最著名的兩種演算法是Dijkstra演算法和A*演算法。在這裡我們將重點放在Dijkstra演算法的實作。 Dijkstra演算法的基
 遞歸在 C++ 資料結構中的妙用:棧和樹的實現
May 04, 2024 pm 01:54 PM
遞歸在 C++ 資料結構中的妙用:棧和樹的實現
May 04, 2024 pm 01:54 PM
遞歸在C++資料結構中的應用:棧:透過後進先出(LIFO)結構遞歸實作棧。樹:透過分層結構遞歸實現樹,支援插入和深度計算等操作。遞歸為處理巢狀結構提供了簡潔且有效率的解決方案,使資料結構的實作更加直覺且易於維護。
 深入探索Java中樹和圖的非線性資料結構應用和實作方法
Dec 26, 2023 am 10:22 AM
深入探索Java中樹和圖的非線性資料結構應用和實作方法
Dec 26, 2023 am 10:22 AM
理解Java中的樹和圖:探索非線性資料結構的應用與實作引言在電腦科學中,資料結構是電腦中儲存、組織和管理資料的方式。資料結構可分為線性資料結構和非線性資料結構。樹和圖是非線性資料結構中最常用的兩種類型。本文將重點放在Java中樹和圖的概念、應用和實現,並給出具體的程式碼範例。樹的概念與應用樹是一種抽象資料類型,由節點和邊組成的集合。樹的每個節點包含一個數
 使用佛洛伊德-沃沙爾演算法找到任兩個節點之間的最短路徑
Sep 20, 2023 pm 02:21 PM
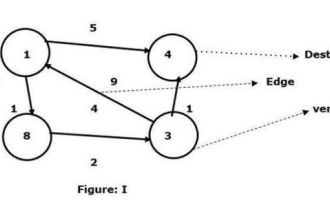
使用佛洛伊德-沃沙爾演算法找到任兩個節點之間的最短路徑
Sep 20, 2023 pm 02:21 PM
C++有一個宏,它被定義為一段程式碼或期望的值,並且每當使用者需要時,它將被重複使用。佛洛伊德-沃爾夏爾演算法是在給定的加權圖中找到所有頂點對之間最短路徑的過程。該演算法遵循動態規劃的方法來找到最小權重圖。讓我們透過圖表來理解佛洛伊德-沃爾夏爾演算法的意義-以頂點1為來源,頂點4為目的地,求它們之間的最短路徑。我們已經看到有兩條路徑可以連接到目標頂點4。1->4–邊的權重為51->8->3->4–邊權重(1+2+1)為4。在給定的圖I中,我們看到兩個頂點之間連接的最小邊。所以這裡頂點
 PHP演算法設計想法:如何實現圖的最短路徑問題的高效解決方案?
Sep 19, 2023 pm 03:43 PM
PHP演算法設計想法:如何實現圖的最短路徑問題的高效解決方案?
Sep 19, 2023 pm 03:43 PM
PHP演算法設計想法:如何實現圖的最短路徑問題的高效解決方案?在實際開發中,我們經常需要解決最短路徑問題,例如在地圖導航、網路路由、物流配送等領域。而圖的最短路徑演算法是解決這類問題的關鍵。圖由一組頂點和一組邊組成。頂點表示節點,邊表示節點之間的關係。最短路徑問題就是要找到連接兩個節點的最短路徑。在PHP中,我們可以使用多種演算法來解決最短路徑問題,其中最著名的演算法
 使用C++實作刪除所有不在任何路徑上且路徑和小於k的節點
Sep 04, 2023 am 10:17 AM
使用C++實作刪除所有不在任何路徑上且路徑和小於k的節點
Sep 04, 2023 am 10:17 AM
在這個問題中,我們有一個二元樹,其從根節點到葉節點的路徑是完全定義的。從根節點到葉子節點的所有節點總和必須大於或等於k。所以我們需要刪除路徑中總和小於k的所有節點。這裡要記住的重要一點是,一個節點可能是許多路徑的一部分,因此只有當所有路徑的總和left的總和為10+20+5,即25,小於150,我們需要對其進行修剪並刪除5 。之後,讓我們評估10->30->40。它小於150,所以刪除40。現在我們看到另一條路徑10->20->35->50,總和115小於150,所以
 C++程式以移除不滿足路徑和大於等於k的節點
Sep 14, 2023 am 11:25 AM
C++程式以移除不滿足路徑和大於等於k的節點
Sep 14, 2023 am 11:25 AM
在這個問題中,我們有一個二元樹,其從根節點到葉節點的路徑是完全定義的。從根節點到葉節點的所有節點的總和必須大於或等於常數值k。因此,我們需要刪除那些總和小於k的路徑中的所有節點,這樣樹中剩餘的路徑將大於k。這裡要記住的重要一點是,一個節點可能是許多路徑的一部分,因此只有當通往該節點的所有路徑的總和left的總和為10+20+5,即25,小於150,我們需要對其進行修剪並刪除5。之後,讓我們評估10->30->40。它小於150,因此刪除40。現在我們看到另一條路徑10->20-






