一個矩陣機率問題?

這裡我們將會看到一個矩陣機率問題。我們有一個矩形矩陣。我們可以以相同的機率從當前單元格移動四個方向。這四個方向是左、右、上、下。我們要計算從位置M[i,j]開始N次移動後的機率。
這裡我們要做一些與DFS相關的事情。我們將從目前房間開始遞歸遍歷四個可能的房間。然後我們就計算少走一步的機率。由於四個方向的機率相等,因此每個方向將貢獻總機率的 0.25。如果跨越矩陣邊界,我們將返回0,當N次移動完成時,將返回1。讓我們看看演算法來獲得這個想法。
演算法
matProb(m, n, x, y, N)
Begin if x,y is not in matrix boundary m, n, then return 0 if N is 0 , then return 1 prob := 0 prob := prob + matProb(m, n, x-1, y, N-1) * 0.25 prob := prob + matProb(m, n, x+1, y, N-1) * 0.25 prob := prob + matProb(m, n, x, y+1, N-1) * 0.25 prob := prob + matProb(m, n, x, y-1, N-1) * 0.25 return prob End
範例
#include<iostream>
using namespace std;
bool isSafe(int x, int y, int m, int n) { //function to check whether (x,y)
is in matrix or not
if(x >= 0 && x < m && y >= 0 && y < n){
return true;
}
return false;
}
double matProb(int m, int n, int x, int y, int N) {
if (!isSafe(x, y, m, n)) //if coundary is crossed
return 0.0;
if (N == 0) //when N is 0, or N is completed, return 1
return 1.0;
double probability = 0.0;
probability += matProb(m, n, x - 1, y, N - 1) * 0.25; //move left
probability += matProb(m, n, x, y + 1, N - 1) * 0.25; //move up
probability += matProb(m, n, x + 1, y, N - 1) * 0.25; //move right
probability += matProb(m, n, x, y - 1, N - 1) * 0.25; //move down
return probability;
}
int main() {
int m = 7, n = 8;
int x = 1, y = 1;
int N = 4;
cout << "Matrix Probability is " << matProb(m, n, x, y, N);
}輸出
Matrix Probability is 0.664062
以上是一個矩陣機率問題?的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
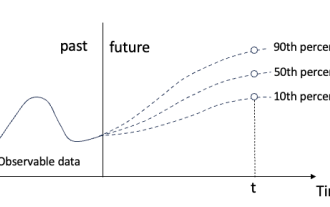 用於時間序列機率預測的分位數迴歸
May 07, 2024 pm 05:04 PM
用於時間序列機率預測的分位數迴歸
May 07, 2024 pm 05:04 PM
不要改變原內容的意思,微調內容,重寫內容,不要續寫。 「分位數迴歸滿足此需求,提供具有量化機會的預測區間。它是一種統計技術,用於模擬預測變數與反應變數之間的關係,特別是當反應變數的條件分佈命令人感興趣時。 ⼀組迴歸變數X與被解釋變數Y的分位數之間線性關係的建模⽅法。現有的迴歸模型其實是研究被解釋變數與解釋變數之間關係的一種方法。他們關註解釋變數與被解釋變數之間的關
 探索人工智慧歷史與矩陣:人工智慧教學(二)
Nov 20, 2023 pm 05:25 PM
探索人工智慧歷史與矩陣:人工智慧教學(二)
Nov 20, 2023 pm 05:25 PM
在本系列的第一篇文章中,我們討論了人工智慧、機器學習、深度學習、資料科學等領域的關聯和差異。我們也為整個系列將使用的程式語言、工具等做出了一些艱難的選擇。最後,我們也介紹了一點矩陣的知識。在本文中,我們將深入討論人工智慧的核心——矩陣。不過在此之前,我們先來了解一下人工智慧的歷史我們為什麼需要了解人工智慧的歷史呢?歷史上曾出現過多次人工智慧熱潮,但在許多情況下,對人工智慧潛力的巨大期望都未能達成。了解人工智慧的歷史,有助於讓我們看清這次人工智浪潮是會創造奇蹟,抑或只是另一個即將破滅的泡沫。我們
 聚類演算法中的聚類效果評估問題
Oct 10, 2023 pm 01:12 PM
聚類演算法中的聚類效果評估問題
Oct 10, 2023 pm 01:12 PM
聚類演算法中的聚類效果評估問題,需要具體程式碼範例聚類是一種無監督學習方法,透過對資料進行聚類,將相似的樣本歸為一類。在聚類演算法中,如何評估聚類的效果是一個重要的問題。本文將介紹幾種常用的聚類效果評估指標,並給出對應的程式碼範例。一、聚類效果評估指標輪廓係數(SilhouetteCoefficient)輪廓係數是透過計算樣本的緊密度和與其他簇的分離度來評估聚類效
 教你如何診斷常見問題的iPhone故障
Dec 03, 2023 am 08:15 AM
教你如何診斷常見問題的iPhone故障
Dec 03, 2023 am 08:15 AM
iPhone以其強大的性能和多方面的功能而聞名,它不能倖免於偶爾的打嗝或技術困難,這是複雜電子設備的共同特徵。遇到iPhone問題可能會讓人感到沮喪,但通常不需要警報。在這份綜合指南中,我們旨在揭開與iPhone使用相關的一些最常遇到的挑戰的神秘面紗。我們的逐步方法旨在幫助您解決這些常見問題,提供實用的解決方案和故障排除技巧,讓您的裝置恢復到最佳工作狀態。無論您是面對一個小故障還是更複雜的問題,本文都可以幫助您有效地解決這些問題。一般故障排除提示在深入研究具體的故障排除步驟之前,以下是一些有助於
 解決jQuery無法取得表單元素值的方法
Feb 19, 2024 pm 02:01 PM
解決jQuery無法取得表單元素值的方法
Feb 19, 2024 pm 02:01 PM
解決jQuery.val()無法使用的問題,需要具體程式碼範例對於前端開發者,使用jQuery是常見的操作之一。其中,使用.val()方法來取得或設定表單元素的值是非常常見的操作。然而,在一些特定的情況下,可能會出現無法使用.val()方法的問題。本文將介紹一些常見的情況以及解決方案,並提供具體的程式碼範例。問題描述在使用jQuery開發前端頁面時,有時候會碰
 弱監督學習中的標籤獲取問題
Oct 08, 2023 am 09:18 AM
弱監督學習中的標籤獲取問題
Oct 08, 2023 am 09:18 AM
弱監督學習中的標籤獲取問題,需要具體程式碼範例引言:弱監督學習是一種利用弱標籤進行訓練的機器學習方法。與傳統的監督學習不同,弱監督學習只需利用較少的標籤來訓練模型,而不是每個樣本都需要有準確的標籤。然而,在弱監督學習中,如何從弱標籤中準確地獲取有用的信息是一個關鍵問題。本文將介紹弱監督學習中的標籤獲取問題,並給出具體的程式碼範例。弱監督學習中的標籤獲取問題簡介:
 Python程式使用多維數組相乘兩個矩陣
Sep 11, 2023 pm 05:09 PM
Python程式使用多維數組相乘兩個矩陣
Sep 11, 2023 pm 05:09 PM
矩陣是按行和列排列的一組數字。 m行n列的矩陣稱為mXn矩陣,m和n稱為其維度。矩陣是一個二維數組,在Python中使用列表或NumPy數組創建。一般來說,矩陣乘法可以透過將第一個矩陣的行乘以第二個矩陣的列來完成。這裡,第一矩陣的列數應等於第二矩陣的行數。輸入輸出場景假設我們有兩個矩陣A和B,這兩個矩陣的維度分別為2X3和3X2。相乘後得到的矩陣將有2行1列。 [b1,b2][a1,a2,a3]*[b3,b4]=[a1*b1+a2*b2+a3*a3][a4,a5,a6][b5,b6][a4*b2+a
 機器學習模型的泛化能力問題
Oct 08, 2023 am 10:46 AM
機器學習模型的泛化能力問題
Oct 08, 2023 am 10:46 AM
機器學習模型的泛化能力問題,需要具體程式碼範例隨著機器學習的發展和應用越來越廣泛,人們越來越關注機器學習模型的泛化能力問題。泛化能力指的是機器學習模型對未標記資料的預測能力,也可以理解為模型在真實世界中的適應能力。一個好的機器學習模型應該具有較高的泛化能力,能夠對新的數據做出準確的預測。然而,在實際應用中,我們經常會遇到模型在訓練集上表現良好,但在測試集或真實






