在圖論中，弄清楚由陣列建立並滿足某些條件的圖是否有環是一項非常重要的任務。圖表是一種顯示事物如何連結在一起的想像方式。它被用在很多地方，例如電腦網路和社交網路。本文討論了圖構造的條件、BFS 和 DFS 演算法，並逐步指導如何識別無向圖中的循環。
圖論中基於數組的方法將頂點和邊存儲在數組中，這使得它們易於在演算法中使用和使用。從空圖開始，根據數組中的信息一次添加一個頂點和邊，這是進一步探索的基礎，例如循環檢測，這對於理解圖如何連結以及是否存在循環非常重要。
圖是由陣列建構的，其中陣列表示一組頂點及其連接或邊。
陣列的每個元素對應圖中的一個頂點
#陣列中每個元素的值表示它所連接的頂點（其相鄰頂點）的索引。
陣列的索引代表頂點本身，其對應的值代表它所連接的頂點。
在建立圖表之前檢查陣列是否有效並滿足所需條件。
確保陣列不為空並且至少包含一個元素來建立頂點。
驗證陣列是否只包含非負整數，因為負值或無效資料無法表示有效的頂點或邊
確保陣列索引在適當的範圍內。它們應該從 0 開始到 n-1，其中 n 是圖中的頂點總數。
確認數組中的值（連接）也在0到n-1的有效範圍內，確保它們對應於現有的頂點
#檢查是否有重複連接或自循環，因為它們違反了有效圖表的條件
驗證沒有遺失連接，這表示所有頂點都連接起來形成完整的圖或連接的元件
深度優先搜尋 (DFS) 用於探索圖的頂點和邊，方法是在轉身之前盡可能深入每個分支
procedure DFS(graph, start_vertex, visited)
if start_vertex is not in visited:
mark start_vertex as visited
process start_vertex (e.g., check for cycles)
for each neighbor in graph[start_vertex]:
if neighbor is not in visited:
DFS(graph, neighbor, visited)
end if
end procedure
pocedure DFS_Traversal(graph)
visited = empty set
for each vertex in graph:
if vertex is not in visited:
DFS(graph, vertex, visited)
end for
end procedure
廣度優先搜尋 (BFS) 是一種圖遍歷演算法，一次一層地遍歷圖的所有頂點。這使得它成為在圖表中尋找週期的好方法
procedure BFS(graph, start_vertex):
create an empty queue Q
create a set visited to keep track of visited vertices
enqueue start_vertex into Q
add start_vertex to visited set
while Q is not empty:
current_vertex = dequeue from Q
for each neighbor_vertex of current_vertex:
if neighbor_vertex is not in visited set:
enqueue neighbor_vertex into Q
add neighbor_vertex to visited set
else:
// A cycle is detected, return true
return true
// No cycle found, return false
return false
時間複雜度
#BFS 和 DFS 的時間複雜度都是 O(V E)，其中 V 是頂點數，E 是邊數。
空間複雜度
#BFS 和 DFS 的時間複雜度為 O(V)。
讓我們考慮一個帶有圖表的範例
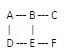
從一個空集合開始監視造訪過的頂點
Visited set: {}
選擇任意頂點作為循環偵測過程的起點。我們選擇頂點 A。
Visited set: {A}
Current Vertex: A
檢查目前頂點 (A) 的相鄰頂點。在本例中，A 的鄰居是 B 和 D。將它們新增至存取集中，並將 A 標識為其父節點
Visited set: {A, B, D}
Current Vertex: A
Parent of B: A
Parent of D: A
B 是存取集中的下一個存取頂點。
Visited set: {A, B, D}
Current Vertex: B
Parent of B: A
探索 B 的周圍環境。 B 的直接鄰居是 A、C 和 E。 A 已經在存取頂點集合中，但它不是 B 的父節點，因此不構成環。
Visited set: {A, B, D, C, E}
Current Vertex: B
繼續到下一個訪問的頂點，即 D。
Visited set: {A, B, D, C, E}
Current Vertex: D
Parent of D: A
發現 D 的熟人。 A 和 E 是 D 的最近鄰居。由於 A 已經包含在存取集中且是 D 的父代，因此必須有一條邊 (D -> A) 將 D 連接到其父代。這表示該圖包含一個循環。
Cycle detected! There is an edge (D -> A) forming a cycle
過程到這裡就結束了，我們已經使用BFS成功偵測到了圖中的環路 即（A->B->E->D->A）。
總之，對於許多應用程式來說，能夠在根據給定參數從陣列建立的圖中找到循環非常重要。無論您使用 DFS 還是 BFS，此過程都有助於找到可能的循環並解決涉及網路、電路和關係的現實問題。有效的循環檢測可以提高演算法的速度並確保數據正確。
以上是檢查根據給定條件從數組建立的圖是否包含循環的詳細內容。更多資訊請關注PHP中文網其他相關文章！
