給定半徑的n邊正多邊形的面積是多少?
在這裡,我們將看到如何計算給定半徑的n邊正多邊形的面積。這裡的半徑是從任一頂點到中心的距離。為了解決這個問題,我們從中心向一邊畫了一條垂線。假設每條邊的長度為'a'。垂線將邊分成兩部分,每部分的長度為a/2。垂線和一個半徑形成一個角度x。假設半徑的長度為h。
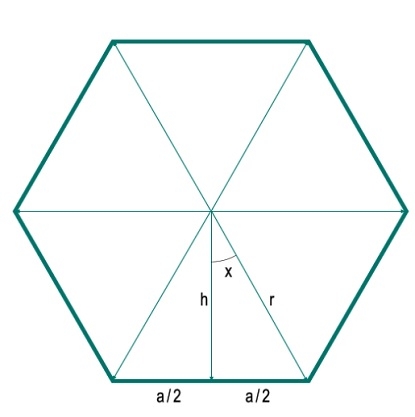
在這裡,我們可以看到多邊形被分成N個相等的三角形。因此,對於任何具有N條邊的多邊形,將被分成N個三角形。因此,中心的角度為360度。這被分成360°/N個不同的角度(這裡360°/6 = 60°)。因此,角度x為180°/N。現在我們可以使用三角方程式輕鬆得到h和a。
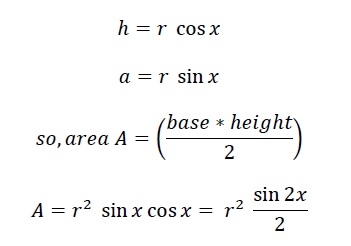
現在整個多邊形的面積為N*A。
範例
#include <iostream>
#include <cmath>
using namespace std;
float polygonArea(float r, int n){
return ((r * r * n) * sin((360 / n) * 3.1415 / 180)) / 2; //convert
angle to rad then calculate
}
int main() {
float rad = 9.0f;
int sides = 6;
cout << "Polygon Area: " << polygonArea(rad, sides);
}輸出
Polygon Area: 210.44
以上是給定半徑的n邊正多邊形的面積是多少?的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
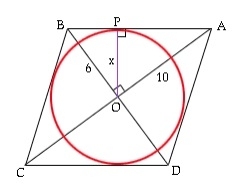 內切於菱形的圓的面積是多少?
Sep 05, 2023 am 08:25 AM
內切於菱形的圓的面積是多少?
Sep 05, 2023 am 08:25 AM
菱形內切圓與其四邊和四個端點相切。菱形的邊與圓相切。這裡,r是使用a和給定值的對角線找到的半徑。現在是面積三角形AOB=½*OA*OB=½*AB*r(兩者皆使用公式½*b*h)。 ½*a/2*b/2=½*(√(a2/4+b2/4))*ra*b/8=√(a2+b2)*r/4r=a*b/2√(a2 +b2)圓面積=π*r*r=π*(a2*b2)/4(a2support>+b2)範例菱形5和10的對角線。面積為15.700000範例程式碼 即時示範#include<stdio.h>intma
 cad面積怎麼標註
Mar 14, 2023 am 11:30 AM
cad面積怎麼標註
Mar 14, 2023 am 11:30 AM
cad面積標註的方法:1、開啟cad,點選“繪圖”,繪製圖形;2、輸入“AREA”指令回車;3、選取區域;4、按空白鍵,顯示該區域的面積;5、輸入指令“T”,然後在該區域內輸入面積的大小即可。
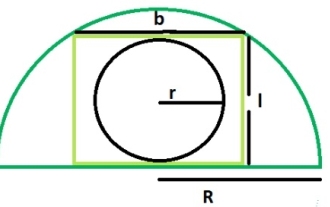 在一個內接於半圓的矩形中的圓的面積是多少?
Sep 13, 2023 am 08:45 AM
在一個內接於半圓的矩形中的圓的面積是多少?
Sep 13, 2023 am 08:45 AM
一個內切於矩形的圓與矩形的較長邊相切,即長度與圓相切。一個內切於半圓的矩形在半圓的弧上接觸兩點。矩形的寬度等於圓的直徑。如果R是半圓的半徑。矩形的長度=√2R/2矩形的寬度=R/√2內切圓的半徑為r=b/2=R/2√2使用這個公式我們可以計算出內切於內切於半圓的矩形的圓的面積,面積=(π*r2)=π*R/8範例 示範#include<stdio.h>intmain(){&
 七邊形數
Sep 24, 2023 am 10:33 AM
七邊形數
Sep 24, 2023 am 10:33 AM
Aheptagonalnumberisanumberwhichcanberepresentedasaheptagon.Aheptagonisapolygonwith7sides.Aheptagonalnumbercanberepresentedasacombinationofsuccessivelayersofheptagon(7-sidedpolygon).Heptagonalnumbercanbebetterexpexpmedwiththebelowgures.第一個七邊形數是第一個七邊形數。因此,
 圓扇形的面積是多少?
Aug 30, 2023 am 08:33 AM
圓扇形的面積是多少?
Aug 30, 2023 am 08:33 AM
圓扇形,也稱為圓扇區/圓的扇區,是由兩個半徑之間的弧線所圍成的圓的一部分。這個區域被兩個半徑和一個弧線所包圍。為了找出內切的面積,我們需要找出兩個半徑之間的角度。總面積等於360度的角度。為了求出一個角度的面積,我們將面積乘以θ/360。這給出了內切部分的面積。其中θ是兩個半徑之間的角度(以度為單位)。圓扇形的面積=π*r*r*(θ/360)。範例半徑為5,角度為60度的圓扇形的面積為13.083。面積=(3.14*5*5)*(60/360)=13.03範例程式碼 演示#incl
 在Java中找到一個內切於正方形的圓的面積
Aug 19, 2023 pm 04:53 PM
在Java中找到一個內切於正方形的圓的面積
Aug 19, 2023 pm 04:53 PM
圓是圍繞形狀的二維圖,沒有角。每個圓都有一個原點,圓上的每個點與原點的距離相等。圓中原點與點之間的距離稱為圓的半徑。同樣,如果我們從
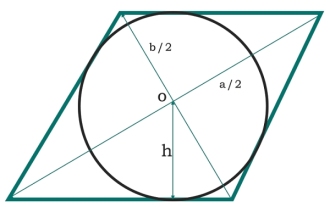 在C程式中,圓內接於菱形的面積是多少?
Sep 01, 2023 pm 09:29 PM
在C程式中,圓內接於菱形的面積是多少?
Sep 01, 2023 pm 09:29 PM
在這裡,我們將看到一個內接於菱形的圓的面積。菱形的對角線分別為'a'和'b'。圓的半徑為h。兩條對角線形成了四個相等的三角形。每個三角形都是直角三角形,因此它們的面積是-菱形的每條邊都是斜邊-因此,圓的面積為-例子#include<iostream>#include<cmath>usingnamespacestd;floatarea(floata,floatb) { if(a<0||b<0)//ifthevaluesaren
 CAD看圖王怎麼測量圖形的面積 CAD看圖王測量圖形面積的步驟
Mar 13, 2024 pm 01:43 PM
CAD看圖王怎麼測量圖形的面積 CAD看圖王測量圖形面積的步驟
Mar 13, 2024 pm 01:43 PM
CAD看圖王怎麼測量圖形的面積? CAD看圖王是一款非常好用的可以看工程圖的軟體,這個軟體功能非常多,各種格式的圖面都可以打開來看。如果我們在看圖面的時候,發現有些圖形的面積測量錯誤或有些圖形忘記測量面積,我們就可以用這個軟體來測量圖形的面積。那麼該如何對圖形的面積進行測量呢,下面本站小編整理了一個CAD看圖王測量圖形面積的步驟供大家參考。 CAD看圖王測量圖形面積的步驟 1、首先CAD看圖王APP中開啟圖面文件,以有圓弧圖形的圖面為例,測量此圖形面積。 2、打開圖紙後在軟體介面下方






